Lý Thuyết Hình Thang | SGK Toán Lớp 8
Có thể bạn quan tâm
1. Các kiến thức cần nhớ
Hình thang
Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
Hai góc kề một cạnh bên của hình thang có tổng bằng ${180^0}$
Nhận xét:
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
+ Hình thang vuông là hình thang có một góc vuông.
Ví dụ 1:

\(ABCD\) là hình thang. Khi đó:
+ \(AB{\rm{//}}CD\) , \(AB,CD\) là hai đáy, \(AD,BC\) là cạnh bên.
+ \(\widehat A + \widehat D = \widehat B + \widehat C = 180^\circ \)
+ Nếu $AD{\rm{//}}BC \Leftrightarrow \left\{ \begin{array}{l}AD = BC\\AB = CD\end{array} \right.$
+ Nếu \(AB = CD \Leftrightarrow \left\{ \begin{array}{l}AD = BC\\AD{\rm{//}}BC\end{array} \right.\)
Hình thang vuông: \(ABCD\) là hình thang có \(\widehat A = 90^\circ \) thì \(ABCD\) là hình thang vuông.
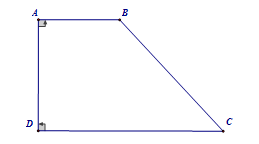
Hình thang cân
Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
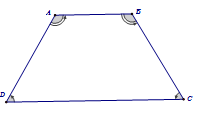
Tính chất:
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Dấu hiệu nhận biết:
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau là hình thang cân.
Ví dụ:
+ \(ABCD\) là hình thang cân thì \(AD = BC;\,AC = BD\)
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat D = \widehat C\end{array} \right.\) \( \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\\widehat A = \widehat B\end{array} \right.\) \( \Leftrightarrow ABCD\) là hình thang cân.
+ Tứ giác \(ABCD\) có \(\left\{ \begin{array}{l}AB{\rm{//}}CD\\AC = BD\end{array} \right.\) \( \Leftrightarrow ABCD\) là hình thang cân.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh và tính các góc của hình thang, hình thang vuông hình thang cân dựa vào tính chất hình.
Phương pháp:
Ta sử dụng các kiến thức:
+ Tính chất của hình thang, hình thang vuông, hình thang cân (ở trên)
+ Tổng bốn góc của một tứ giác bằng$360^\circ $ .
+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
+ Hai góc kề một cạnh bên của hình thang bằng ${180^0}$ .
Dạng 2: Chứng minh một tứ giác là hình thang, hình thang vuông, hình thang cân
Phương pháp:
Ta sử dụng định nghĩa và các dấu hiệu nhận biết để chứng minh
Từ khóa » Tính Chất Của Hình Thang Lớp 8
-
Hình Thang: Lý Thuyết Và Các Dạng Bài Thường Gặp | Giải Toán 8
-
Lý Thuyết Hình Thang Hay, Chi Tiết | Toán Lớp 8
-
Hình Học 8 Bài 2: Hình Thang - HOC247
-
Lý Thuyết Hình Thang Toán 8
-
Định Nghĩa Hình Thang, Hình Thang Vuông - Hình Học 8 - Toán Lớp 8
-
Lý Thuyết Toán 8: Bài 2. Hình Thang - TopLoigiai
-
Tìm Hiểu Về Tính Chất Hình Thang Và Các Dạng Toán Thường Gặp - VOH
-
Tính Chất Hình Thang Vuông - Diện Tích Hình Thang Cân
-
Định Nghĩa, Tính Chất, Dấu Hiệu Nhận Biết Các Hình Học Phẳng Lớp 8
-
Toán 8 Bài 2: Hình Thang
-
ĐỊNH NGHĨA HÌNH THANG-TÍNH CHẤT HÌNH THANG ... - YouTube
-
Hình Học Lớp 8 Bài 2 Hình Thang Ngắn Gọn Và Chi Tiết - Soạn Bài Tập
-
Lý Thuyết & Giải Bài Tập SGK Bài 2: Hình Thang - Chương I - Toán 8
-
Tổng Hợp Kiến Thức Cơ Bản Về Hình Thang Và Hình Thang Cân