Lý Thuyết Lũy Thừa | SGK Toán Lớp 12
Có thể bạn quan tâm
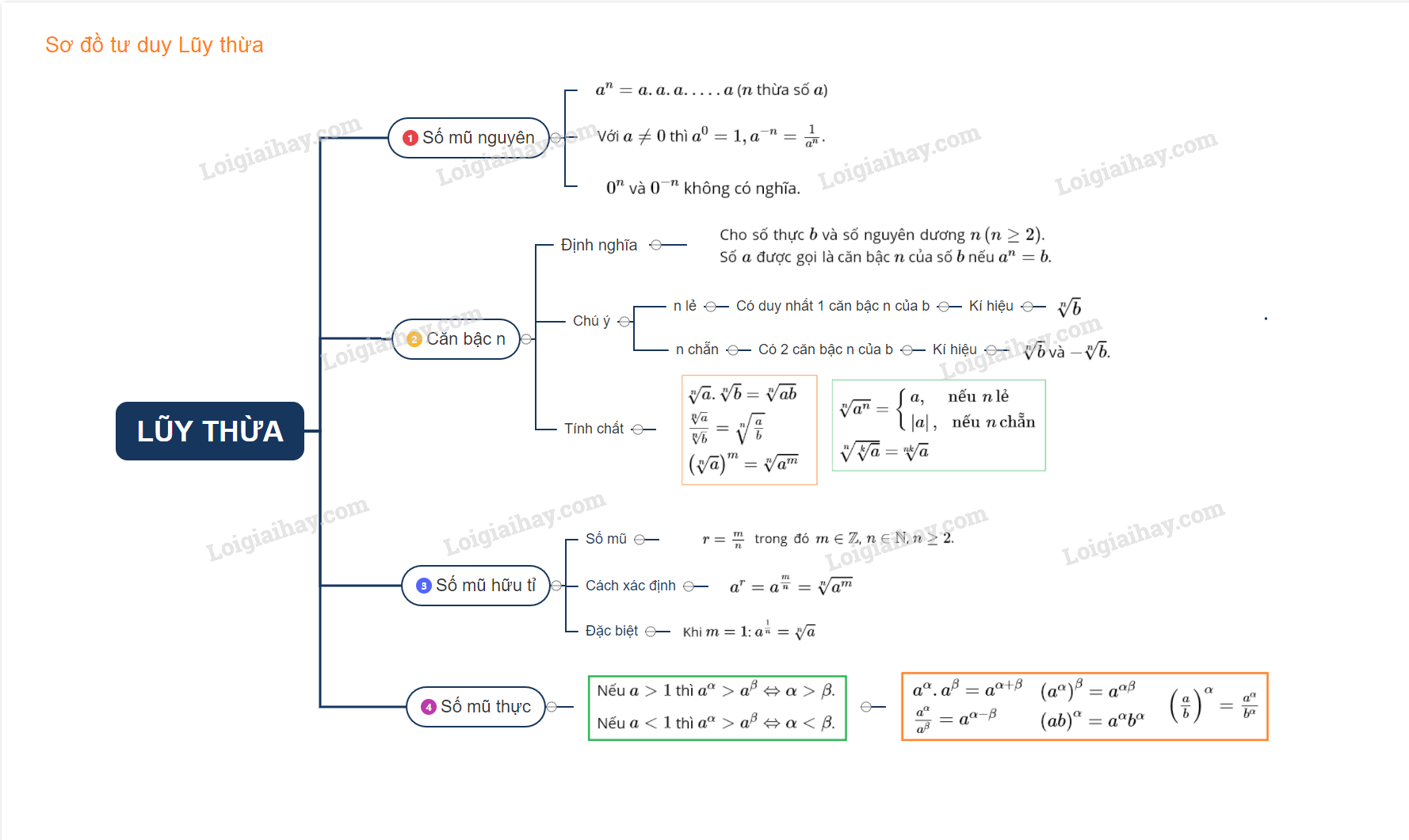
I. KHÁI NIỆM LŨY THỪA
1. Lũy thừa với số mũ nguyên
Định nghĩa
Cho \(n\) là một số nguyên dương.
Với \(a\) là một số thực tùy ý, lũy thừa bậc \(n\) của \(a\) là tích của \(n\) thừa số \(a\).
\({a^n} = a.a.a.....a\) (\(n\) thừa số \(a\))
Với \(a \ne 0\) thì \({a^0} = 1,{a^{ - n}} = \dfrac{1}{{{a^n}}}\).
Chú ý
\({0^n}\) và \({0^{ - n}}\) không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
2. Căn bậc \(n\)
a) Định nghĩa
Cho số thực \(b\) và số nguyên dương \(n\left( {n \ge 2} \right)\). Số \(a\) được gọi là căn bậc \(n\) của số \(b\) nếu \({a^n} = b\).
b) Chú ý
+) Với \(n\) lẻ và \(b \in \mathbb{R}\) thì có duy nhất một căn bậc \(n\) của \(b\), kí hiệu \(\sqrt[n]{b}\).
+) Với \(n\) chẵn và:
\(b < 0\) thì không tồn tại căn bậc \(n\) của \(b\).
\(b = 0\) thì có duy nhất một căn bậc \(n\) của \(b\) là số \(0\).
\(b > 0\) thì có hai căn trái dấu, kí hiệu \(\sqrt[n]{b}\) và \( - \sqrt[n]{b}\).
c) Tính chất
\(\begin{array}{l}\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\\\dfrac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\dfrac{a}{b}}}\\{\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\\\sqrt[n]{{{a^n}}} = \left\{ \begin{array}{l}a,\,\,\,\,\,\,\,\text{nếu} \,\,n \,\text{lẻ}\\\left| a \right|,\,\,\,\,\text{nếu}\,\,n\,\text{chẵn}\end{array} \right.\\\sqrt[n]{{\sqrt[k]{a}}} = \sqrt[{nk}]{a}\end{array}\)
Ví dụ
\(\sqrt[3]{{ - 4}}.\sqrt[3]{{54}} = \sqrt[3]{{\left( { - 4} \right).54}} = \sqrt[3]{{ - 216}} = - 6\)
3. Lũy thừa với số mũ hữu tỉ
Cho số thực \(a\) dương và số hữu tỉ \(r = \dfrac{m}{n}\), trong đó \(m \in \mathbb{Z}\), \(n \in \mathbb{N}\), \(n \ge 2\).
Lũy thừa của số \(a\) với số mũ \(r\) là số \({a^r}\) xác định bởi
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
Đặc biệt: Khi \(m=1\): \({a^{\frac{1}{n}}} = \sqrt[n]{a}\)
Ví dụ:
\({16^{ - \frac{3}{4}}} = \sqrt[4]{{{{16}^{ - 3}}}} = \dfrac{1}{{\sqrt[4]{{{{16}^3}}}}}\) \( = \dfrac{1}{{{{\left( {\sqrt[4]{{16}}} \right)}^3}}} = \dfrac{1}{{{2^3}}} = \dfrac{1}{8}\)
II. TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC
Cho \(a,b\) là những số thực dương; \(\alpha ,\beta \) là những số thực tùy ý. Khi đó ta có:
\(\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\\\dfrac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }}\\{\left( {ab} \right)^\alpha } = {a^\alpha }{b^\alpha }\\{\left( {\dfrac{a}{b}} \right)^\alpha } = \dfrac{{{a^\alpha }}}{{{b^\alpha }}}\end{array}\)
Nếu \(a > 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \).
Nếu \(a < 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \).
Ví dụ: Rút gọn biểu thức: \(A = \dfrac{{{a^{\sqrt 2 + 1}}.{a^{3 - \sqrt 2 }}}}{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}\)
Ta có:
\(\begin{array}{l}A = \dfrac{{{a^{\sqrt 2 + 1}}.{a^{3 - \sqrt 2 }}}}{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}} = \dfrac{{{a^{\sqrt 2 + 1 + 3 - \sqrt 2 }}}}{{{a^{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}}}\\ = \dfrac{{{a^4}}}{{{a^{3 - 1}}}} = {a^2}\end{array}\)
Loigiaihay.com
Từ khóa » Các Bài Toán Lũy Thừa 12
-
Cách Giải Bài Tập Về Lũy Thừa Cực Hay - Toán Lớp 12
-
Bài Tập Lũy Thừa Trong đề Thi Đại Học Có Lời Giải (4 Dạng)
-
Giải Toán 12 Bài 1. Lũy Thừa - Giải Bài Tập
-
Các Dạng Bài Tập Hàm Số Mũ, Lũy Thừa, Lôgarit Chọn Lọc - Toán Lớp 12
-
Các Dạng Bài Tập Lũy Thừa, Mũ Và Lôgarit
-
Bài Tập Công Thức Lũy Thừa, Hàm Số Mũ Logarit Lớp 12 Có đáp án Chi Tiết
-
[Toán 12] Các Dạng Bài Tập Luỹ Thừa - Thầy Nguyễn Công Chính
-
Toán 12 Bài 1: Lũy Thừa - Hoc247
-
Các Dạng Bài Tập Vận Dụng Cao Lũy Thừa Và Hàm Số Lũy Thừa
-
Sách Giải Bài Tập Toán Lớp 12 Bài 1: Lũy Thừa
-
Bí Quyết Chinh Phục Luỹ Thừa Lớp 12 Siêu đơn Giản
-
Toán 12 Bài 1: Lũy Thừa
-
Lũy Thừa - Toán 12
-
Bài Tập Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit