Lý Thuyết, Phương Pháp Giải Bài Tập Chương Lượng Tử ánh Sáng
Có thể bạn quan tâm
LÝ THUYẾT, PHƯƠNG PHÁP GIẢI BÀI TẬP CHƯƠNG LƯỢNG TỬ ÁNH SÁNG
(hay và đầy đủ)
I. HIỆN TƯỢNG QUANG ĐIỆN NGOÀI
1) Thí nghiệm Hertz về hiện tượng quang điện
a) Thí nghiệm
▪ Chiếu chùm ánh sáng tử ngoại phát ra từ hồ quang vào tấm kẽm tích điện âm (tấm kẽm đang thừa electron) gắn trên diện nghiệm ta thấy hai lá của điện nghiệm cụp lại, tấm kẽm mất điện tích âm.
▪ Chắn chùm tia từ ngoại từ hồ quang bằng một tấm kính thì hiện tượng không xảy ra.
▪ Thay tấm kẽm tích điện âm bằng tấm kẽm tích điện dương, hiện tượng cũng không xảy ra. Thay tấm kẽm bằng các kim loại khác tích điện âm hiện tượng xảy ra bình thường.
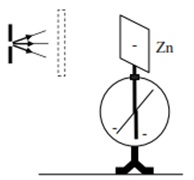
Kết luận:
Khi chiếu chùm ánh sáng thích hợp có bước sóng ngắn vào bề mặt một tấm kim loại thì nó làm cho các electron ở bề mặt tấm kim loai bị bật ra. Hiện tượng đó gọi là hiện tượng quang điện. Các e bị bật ra gọi là các e quang điện.
b) Khái niệm hiện tượng quang điện ngoài
Hiện tượng electron bị bật ra khi chiếu ánh sáng có bước sóng thích hợp vào một tấm kim loại được gọi là hiện tượng quang điện ngoài, hay gọi tắt là hiện tượng quang điện.
2) Thí nghiệm với tế bào quang điện
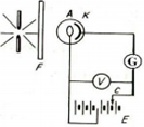
a) Khái niệm về tế bào qung điện
Tế bào quang điện là một bình chân không (đã được hút hết không khí bên trong), gồm có hai điện cực:
▪ Anot là một vòng dây kim loại.
▪ Catot có dạng chỏm cầu bằng kim loại.
▪ Khi chiếu vào catốt của tế bào quang điện ánh sáng đơn sắc có bước sóng thích hợp thì trong mạch xuất hiện một dòng điện gọi là dòng quang điện.
b) Kết quả thí nghiệm
b) Kết quả thí nghiệm
▪ Với mỗi kim loại dùng làm catot, ánh sáng kích thích phải có bước
sóng λ nhỏ hơn một giới hạn λ0 nào đó thì hiện tượng mới xảy ra.
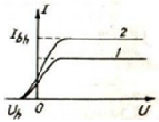
▪ Cường độ dòng quang điện phụ thuộc vào UAK theo đồ thị sau:
+ UAK > 0: Khi UAK tăng thì I tăng, đến giá trị nào đó, I đạt đến giá trị bão hòa. Lúc đó UAK tăng thì I vẫn không tăng.
+ UAK < 0: I không triệt tiêu ngay mà phải đến giá trị UAK = Uh < 0 nào đó.
Chú ý:
▪ Muốn cho dòng quang điện triệt tiêu thì phải đặt giữa AK một hiệu điện thế hãm Uh < 0, trị số của Uh phụ thuộc vào bước sóng λ của chùm sáng kích thích.
▪ Dòng quang điện bão hòa khi tất cả các electron bứt ra khỏi Catot đều đến được Anot.
▪ Cường độ dòng quang điện bão hòa tỉ lệ thuận với cường độ chùm sáng kích thích mà không phụ thuộc vào bước sóng của ánh sáng kích thích.
▪ Độ lớn của Uh được tính từ biểu thức của định lý động năng: \(\frac{mv_{0max}^{2}}{2}=\begin{vmatrix} eU_{h} \end{vmatrix}\) trong đó e = –1,6.10–19 C là điện tích của electron, m = 9,1.10–31kg là khối lượng của electron.
II. CÁC ĐỊNH LUẬT QUANG ĐIỆN
1) Định luật I : (Định luật về giới hạn quang điện)
a) Phát biểu
Đối với mỗi kim loại, ánh sáng kích thích phải có bước sóng λ ngắn hơn hay bằng giới hạn quang điện λ0 của kim loại đó, mới gây ra được hiện tượng quang điện. Biểu thức: λ ≤ λ0
b) Đặc điểm
Giới hạn quang điện của mỗi kim loại (kí hiệu λ0) là đặc trưng riêng cho kim loại đó.
Giới hạn kim loại của một số kim loại hình:
| Tên kim loại | Giới hạn quang điện (λ0) |
| Bạc (Ag) | 0,26 μm |
| Đồng (Cu) | 0,3 μm |
| Kẽm (Zn) | 0,35 μm |
| Nhôm (Al) | 0,36μm |
| Canxi (Ca) | 0,43 μm |
| Natri (Na) | 0,5 μm |
| Kali (K) | 0,55 μm |
| Xesi (Cs) | 0,58 μm |
Chú ý:
Quan sát bảng giá trị giới hạn quang điện của các kim loại điển hình hay dùng ta thấy rằng các kim loại kiềm có giới hạn quang điện khá lớn nên khi chiếu ánh sáng vào hiện tượng quang điện có thể dễ xảy ra hơn với các kim loại Kẽm hay Đồng hơn là các kim loại kiềm.
2) Định luật II : (Định luật về cường độ dòng quang điện bão hòa)
Với ánh sáng kích thích có bước sóng thích hợp (λ ≤ λ0) thì cường độ dòng quang điện bão hòa tỉ lệ với cường độ của chùm sáng kích thích.
3) Định luật III : (Định luật về động năng ban đầu cực đại của các electron quang điện)
Động năng ban đầu cực đại của các electrong quang điện không phụ thuộc vào cường độ của chùm sáng kích thích mà chỉ phụ thuộc vào bước sóng của ánh sáng kich thích và bản chất kim loại dùng làm catốt.
Chú ý:
▪ Kí hiệu động năng ban đầu cực đại là Wđmax thì theo định luật quang điện III ta thấy Wđmax chỉ phụ thuộc vào λ và bản chất kim loại dùng làm Catot, do mỗi kim loại có một giới hạn quang điện nhất định nên nói một cách khác, động năng ban đầu cực đại phụ thuộc vào λ và λ0.
▪ Trong nội dung của chương trình Chuẩn thì chỉ dừng lại ở Định luật quang điện I, các định luật II và III chỉ mang tính tham khảo.
III. THUYẾT LƯỢNG TỬ ÁNH SÁNG
1) Giả thuyết về lượng tử năng lượng Planck
Theo nhà bác học người Đức, Planck, Lượng năng lượng mà mỗi lần một nguyên tử hay phân tử hấp thụ hay phát xạ có giá trị hoàn toàn xác định, được ký hiệu là ε và có biểu thức ε = h.f
Trong đó:
f là tần số của ánh sáng bị hấp thụ hay phát ra
h là một hằng số, được gọi là hằng số Plack có giá trị h = 6,625.10–34 J.s
2) Sự bất lực của thuyết sóng ánh sáng
Theo thuyết sóng ánh thì ánh sáng là một chùm sóng điện từ. Khi đạp vào bề mặt kim loại sẽ làm cho các e ở bề mặt kim loại dao động, cường độ chùm sáng càng lớn thì các e dao động càng mạnh và bật ra ngoài tạo thành dòng quang điện. Do đó bất kì chùm sáng nào có cường độ đủ mạnh cũng gây ra hiện tượng quang điện (trái với định luật I) và động năng ban đầu cực đại của các e chỉ phụ thuộc cường độ của chùm sáng kích thích (trái với định luật III).
3) Thuyết lượng tử ánh sáng
Nội dung của thuyết lượng tử ánh sáng do nhà bác học Anhxtanh nêu lên có 3 nội dung chính: ε
▪ Ánh sáng được tạo thành bởi các hạt gọi là phôtôn, mỗi phôtôn còn gọi là các lượng tử có năng lượng xác định ε = h.f, cường độ của chùm sáng tỉ lệ với số phôtôn phát ra trong 1 giây.
▪ Phôtôn bay với tốc độ c = 3.108m/s dọc theo các tia sáng.
▪ Mỗi lần một nguyên tử hay phân tử phát xạ hay hấp thụ ánh sáng thì chúng phát ra hay hấp thụ phôtôn.
Chú ý:
▪ Những nguyên tử hay phân tử vật chất không hấp thụ hay bức xạ ánh sáng một cách liên tục mà thành từng phần riêng biệt đứt quãng, mỗi phần đó mang một năng lượng hoàn toàn xác định - Chùm sáng là một chùm hạt mỗi hạt là một phôtôn mang một năng lượng xác định.
▪ Khi ánh sáng truyền đi, các lượng tử năng lượng không bị thay đổi, không phụ thuộc cách nguồn sáng xa hay gần.
IV. GIẢI THÍCH CÁC ĐỊNH LUẬT QUANG ĐIỆN
1) Hệ thức Anhxtanh
▪ Anhxtanh coi chùm sáng là chùm hạt, mỗi hạt là một phôtôn mang một năng lượng xác định ε = h.f.
▪ Trong hiện tượng quang điện có sự hấp thụ hoàn toàn phô tôn chiếu tới. Mỗi phôtôn bị hấp thụ sẽ truyền toàn bộ năng lượng của nó cho một electron. Đối với các electron trên bề mặt năng lượng ε này dùng làm hai việc:
- Cung cấp cho electron một công thoát A để thắng lực liên kết trong tinh thể và thoát ra ngoài.
- Cung cấp cho electron một động năng ban đầu cực đại để electron bay đến Anot.
Theo định luật bảo toàn năng lượng ta có ε = hf = A + Wđmax =\(A+\frac{mv_{0max}^{2}}{2}\)
Công thức trên được gọi là hệ thức Anhxtanh.
Chú ý:
Thay công thức tính tần số f = c/λ hoặc động năng theo Uh ta được các hệ quả của hệ thức Anhxtanh
ε = hf = A + Wđmax = \(A+\frac{mv_{0max}^{2}}{2}=A+\begin{vmatrix} eU_{h} \end{vmatrix}\Leftrightarrow \frac{hc}{\lambda }=A+\frac{mv_{0max}^{2}}{2}=A+\begin{vmatrix} eU_{h} \end{vmatrix}\)
Các hằng số : h = 6,625.10–34J.s, c = 3.108 m/s, m = 9,1.10–31kg, e = –1,6.10–19 C.
2) Giải thích các định luật quang điện
a) Giải thích Định luật I
Để xảy ra hiện tượng quang điện, năng lượng một phôtôn phải lớn hơn công thoát A (là năng lượng để giữ các electron ở lại tấm kim loại).
Khi đó ta có \(\varepsilon \geq A\Leftrightarrow hf\geq A\Leftrightarrow \frac{hc}{\lambda }\geq A\Rightarrow \lambda \leq \frac{hc}{A}\) (1)
Đặt \(\lambda_{0} =\frac{hc}{A}\), được gọi là giới hạn quang điện. Khi đó (1) được viết lại là λ ≤ λ0
b) Giải thích Định luật II
Cường độ dòng quang điện bão hòa tỉ lệ với số electron quang điện. Số electron quang điện tỉ lệ với số phô tôn đến đập vào Catot trong một đơn vị thời gian. Số phôton đến đập vào Catot trong một đơn vị thời gian tỉ lệ với cường độ chùm sáng. Vậy cường độ dòng quang điện bão hòa tỉ lệ với cường độ chùm sáng.
c) Giải thích Định luật III
Từ hệ thức Anhxtanh ta có hf = A + Wđmax =\(A+\frac{mv_{0max}^{2}}{2}\Leftrightarrow \frac{hc}{\lambda }=A+\frac{mv_{0max}^{2}}{2}\)
Ta thấy động năng ban đầu cực đại (Wđmax) chỉ phụ thuộc vào λ và A, tức là bước sóng của chùm sáng chiếu vào kim loại và bản chất kim loại làm Catot.
Chú ý:
▪ Từ công thức tính giới hạn quang điện \(\lambda _{0}=\frac{hc}{A }\rightarrow A=\frac{hc}{\lambda _{0}}\), thay vào hệ thức Anhxtanh ta được
\(hf=A+\frac{mv_{0max}^{2}}{2}\Leftrightarrow \frac{hc}{\lambda }=A+\frac{mv_{0max}^{2}}{2}\Leftrightarrow \frac{hc}{\lambda }=\frac{hc} {\lambda_{0}}+\frac{mv_{0max}^{2}}{2}\)
▪ Trong các công thức tính toán thì tích số h.c thường được lặp lại nhiều lần trong các bước tính, để thuận tiện ta lưu giá trị của hằng số này hc = 19,875.10–26
▪ Giá trị của v0max dao động trong khoảng từ 105(m/s) đến 107(m/s).
5) Lưỡng tính sóng hạt của ánh sáng
Hiện tượng giao thoa chứng tỏ ánh sáng có tính chất sóng, hiện tượng quang điện chứng tỏ ánh sáng có tính chất hạt. Vậy ánh sáng có lưỡng tính sóng hạt.
IV. MỘT SỐ VÍ DỤ ĐIỂN HÌNH
Ví dụ 1. Tính năng lượng phôtôn ứng với ánh sáng có bước sóng λ1 = 0,768 μm; λ2 = 0,589 μm; λ3 = 0,444 μm.
Hướng dẫn giải:
Áp dụng công thức tính lượng tử năng lượng ta có
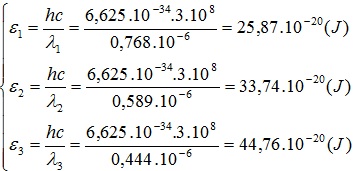
CÁC DẠNG BÀI TẬP VỀ LƯỢNG TỬ ÁNH SÁNG – PHẦN 1
DẠNG 1. TÍNH TOÁN CÁC ĐẠI LƯỢNG LIÊN QUAN TRONG HỆ THỨC ANHXTANH
Cách giải:
Hệ thức Anhxtanh: \(hf=A+\frac{mv_{0max}^{2}}{2}\Leftrightarrow \frac{hc}{\lambda }=A+\frac{mv_{0max}^{2}}{2}\Leftrightarrow \frac{hc}{\lambda }=\frac{hc} {\lambda_{0}}+\frac{mv_{0max}^{2}}{2}\)
▪ Tính λ0: Có thể tính từ hệ thức Anhxtanh hoặc công thức \(\lambda _{0}=\frac{hc}{A}\)
▪ Tính v0max: Có thể tính từ hệ thức hoặc tính theo phương trình \(\frac{mv_{omax}^{2}}{2}=\begin{vmatrix} eU_{h} \end{vmatrix}\rightarrow v_{omax}=\sqrt{\frac{2\begin{vmatrix} eU_{h} \end{vmatrix}}{m}}\)
▪ Tính |Uh|: Tính theo phương trình \(\frac{mv_{omax}^{2}}{2}=\begin{vmatrix} eU_{h} \end{vmatrix}\rightarrow U_{h}=\frac{mv_{omax}^{2}}{2\begin{vmatrix} e \end{vmatrix}}\)
Chú ý: UAK = –Uh thì cường độ dòng quang điện triệt tiêu (I = 0).
▪ Tính λ: \(\varepsilon =\frac{hc}{\lambda }=hf\rightarrow f=\frac{hc}{\varepsilon }=\frac{c}{f}\) hoặc \(\frac{hc}{\lambda }=\frac{hc} {\lambda_{0}}+\frac{mv_{0max}^{2}}{2}\rightarrow \lambda =\frac{2hc\lambda _{0}}{2hc+\lambda _{0}mv_{0max}^{2}}\)
▪ Tính năng lượng ε: \(\varepsilon =hf=\frac{hc}{\lambda }\) hoặc \(\varepsilon =A+\begin{vmatrix} eU_{h} \end{vmatrix}=\frac{hc}{\lambda _{0}}+\frac{mv_{0max}^{2}}{2}\)
Chú ý: (Cách chuyển đổi đơn vị)
Ta biết rằng công của lực điện trường A = q.U, nên đơn vị của công ngoài đơn vị J còn có thể tính theo đơn vị eV.
1eV = 1,6.10–19J và 1J = ( eV ).
Ví dụ 1. Chiếu ánh sáng có bước sóng λ = 0,5 (μm) vào một tấm kim loại dùng làm Catot của tế bào quang điện có công thoát A = 2,27 (eV).
a) Hiện tượng quang điện có xảy ra không?
b) Tính vận tốc ban đầu cực đại của electrong quang điện.
c) Tính hiệu điện thế hãm cần đặt vào để làm dòng quang điện bị triệt tiêu.
Hướng dẫn giải:
a) Để kiểm tra hiện tượng quang điện có xảy ra hay không ta kiểm tra điều kiện λ ≤ λ0
Ta có \(\lambda _{0}=\frac{hc}{A}=\frac{19,875.10^{-26}}{2,27.1,6.10^{-19}}=0,547(\mu m)\rightarrow \lambda < \lambda _{0}\)
Vậy hiện tượng quang điện có xảy ra.
b) Theo hệ thức Anhxtanh: \(\frac{hc}{\lambda }=A+\frac{mv_{0max}^{2}}{2}\_{0max}=\sqrt{\frac{2(\frac{hc}{\lambda }-A)}{m}} =1,94.10^{5}(m/s)\)
c) Từ hệ thức Anhxtanh:\(\frac{hc}{\lambda }=A+\begin{vmatrix} eU_{h} \end{vmatrix}\rightarrow \begin{vmatrix} U_{h} \end{vmatrix}=\sqrt{\frac{\left ( \frac{hc}{\lambda }-A \right )}{\begin{vmatrix} e \end{vmatrix}}}=0,463(V)\)
DẠNG 2. HIỆU SUẤT LƯỢNG TỬ ÁNH SÁNG
Cách giải:
▪ Cường độ dòng quang điện bão hòa \(I_{bh}=\frac{q}{t}=\frac{n\begin{vmatrix} e \end{vmatrix}}{t}\), với n là số electron bật ra khỏi Catot để đến Anot và t là thời gian mà số electron di chuyển. Khi t = 1 (s) thì ta có Ibh = n.|e|
Từ đó ta tính được số electron bứt ra sau khoảng thời gian t là \(n=\frac{I_{bh}}{\begin{vmatrix} e \end{vmatrix}}=\frac{I_{bh}}{1,6.10^{-9}}\)
▪ Chiếu chùm sáng có bước sóng λ vào Catot của tế bào quang điện thì sau khoảng thời gian t công suất phát xạ P của chùm sáng là \(P=\frac{W}{t}=\frac{N\varepsilon }{t}=\frac{N\frac{hc}{\lambda }}{t}=\frac{N.hc}{t.\lambda }\), với N là số phôtôn đập vào Catot trong thời gian t, và W là năng lượng của chùm photon chiếu vào Catot.
Từ đó ta tính được số phôtôn đập vào Catot trong thời gian t là \(N=\frac{P.\lambda .t}{hc}\) . Khi t = 1 (s) thì \(N=\frac{P.\lambda }{hc}\)
▪ Hiệu suất lượng tử:
Là tỉ số giữa số electron bứt ra và số phô tôn đập vào Catot trong khoảng thời gian t.
Ta có công thức tính toán hiệu suất: \(H=\frac{n}{N}=\frac{\frac{I_{bh}}{\begin{vmatrix} e \end{vmatrix}}}{\frac{P\lambda }{hc}}=\frac{I_{bh}.hc}{P.\lambda .\begin{vmatrix} e \end{vmatrix}}\)
Ví dụ 1. Một ngọn đèn phát ra ánh sáng đơn sắc có bước sóng λ = 0,6 μm sẽ phát ra bao nhiêu phôtôn trong 30(s) nếu công suất phát xạ của đèn là 10 (W)?
Hướng dẫn giải:
Theo bài ta có \(P=\frac{W}{t}=\frac{N\varepsilon }{t}= \frac{N\frac{hc}{\lambda }}{t}\rightarrow N=\frac{Pt\lambda }{hc}=\frac{10.30.0,6.10^{-6}}{19,875.10^{-26}}\) (photon)
DẠNG 3. TÍNH ĐIỆN THẾ CỰC ĐẠI CỦA VẬT DẪN CÔ LẬP VỀ ĐIỆN
Cách giải :
Khi chiếu ánh sáng vào một vật dẫn cô lập về điện, thì sau một khoảng thời gian các electron bị bứt ra và vật tích điện dương (đạt được một điện thế). Số electron bị bật ra càng nhiều thì điện thế của vật càng tăng lên và khi vật đạt điện thế cực đại Vmax thì số electron bị bứt ra lại bị hút trở lại. Điện thế của vật không tăng nữa, khi đó giá trị điện thế cực đại chính là độ lớn hiệu điện thế hãm trong tế bào quang điện.
Ta có eVmax = eUh
Theo định lý động năng \(eV_{max}=e\begin{vmatrix} U_{h} \end{vmatrix}=\frac{mv_{0max}^{2}}{2}\)
Chú ý:
▪ Khi chiếu đồng thời các bức xạ có bước sóng λ1, λ2, λ3… vào tấm kim loại và đều có hiện tượng quang điện xảy ra, với mỗi bức xạ sẽ cho một giá trị điện thế cực đại V1max, V2max, V3max…. Khi đó điện thế cực đại của tấm kim loại là Vmax = maxhay một cách dễ nhớ hơn là điện thế Vmax sẽ ứng với bức xạ có bước sóng nhỏ nhất trong các bức xạ.
▪ Xét vật cô lập về điện, có điện thế cực đại Vmax và khoảng cách cực đại dmax mà electron chuyển động trong điện trường cản có cường độ E được tính theo công thức \(eV_{max}=\frac{mv_{0max}^{2}}{2}=\begin{vmatrix} e \end{vmatrix}Ed_{max}\)
Ví dụ 1. Một tấm kim loại có công thoát electron là A = 7,23.10-19 (J).
a) Xác định giới hạn quang điện của kim loại.
b) Dùng tấm kim loại đó đặt cô lập, được rọi sáng đồng thời bởi hai bức xạ, bức xạ thứ nhất có tần số f1 = 1,5.1015 (Hz) và bức xạ thứ hai có bước sóng λ2 = 0,18 (μm). Tính điện thế cực đại trên tấm kim loại.
c) Khi rọi bức xạ có tần số f1 vào tế bào quang điện có catốt được làm bằng kim loại kể trên, để không một electron nào về được anốt thì hiệu điện thế UAK bằng bao nhiêu?
Hướng dẫn giải:
a) Giới hạn quang điện của tấm kim loại \(h_{0}=\frac{hc}{\lambda }\) = 0, 275(μm).
b) Ta có f1 = 1, 5.1015 Hz \(\rightarrow \lambda _{1}=\frac{c}{f_{1}}=\frac{3.10^{8}}{1,5.10^{15}}=0,2(\mu m)\)
Như vậy khi chiếu cả hai bức xạ vào tấm kim loại thì đều có hiện tượng quang điện xảy ra.
Điện thế cực đại tương ứng của các bức xạ là
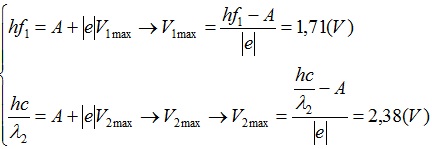
Khi đó điện thế cực đại của tấm kim loại là Vmax = V2max = 2,38 (V).
c) Khi chiếu sáng bằng bức xạ có tần số f1 để không có electron nào đến được Anot thi cần đặt giữa Anot và Katot hiệu điện thế UAK = Uh < 0.
Theo hệ thức Anhxtanh ta có \(hf=A+\begin{vmatrix} eU_{h} \end{vmatrix}\Leftrightarrow \begin{vmatrix} U_{h} \end{vmatrix}=\frac{hf_{1}-A}{\begin{vmatrix} e \end{vmatrix}}=1,71(V)\rightarrow U_{AK}=-1,71(V)\) Vậy cần đặt UAK = –1,71 (V).
Từ khóa » Thuyết Lượng Tử
-
Thuyết Lượng Tử Năng Lượng – Wikipedia Tiếng Việt
-
Thuyết Lượng Tử Ánh Sáng: Lý Thuyết, Công Thức, Bài Tập SGK
-
14/12/1900: Sự Ra đời Của Thuyết Lượng Tử
-
Vật Lý Lượng Tử Là Gì: Nguồn Gốc Và Nguyên Lý
-
Mối Liên Hệ Lạ Thường Giữa Trí Não Và Vật Lý Lượng Tử
-
Lý Thuyết Công Thức Lượng Tử ánh Sáng, Nội Dung Thuyết ... - TopLoigiai
-
Thuyết Lượng Tử ánh Sáng Vật Lý 12 (Lý Thuyết Và Bài Tập)
-
Định Mệnh Nghiệt Ngã Của Người Khai Sáng Thuyết Lượng Tử
-
Thuyết Lượng Tử ánh Sáng. Các ĐL Quang điện – Vật Lí 12 - YouTube
-
Thuyết Lượng Từ Về ánh Sáng Phát Biểu Như Thế Nào ? Công Thức Và ...
-
Thầy Vũ Tuấn Anh - [BUỔI 3] Lý Thuyết Lượng Tử Ánh Sáng - YouTube
-
Theo Thuyết Lượng Tử ánh Sáng, Phát Biểu Nào Sau đây Là Sai?