Lý Thuyết Toán 8: Bài 4. Phương Trình Tích - TopLoigiai

Trang chủ » Học Toán Lớp 8 Bài 4 Phương Trình Tích » Lý Thuyết Toán 8: Bài 4. Phương Trình Tích - TopLoigiai

Có thể bạn quan tâm

Mục lục nội dung Bài 4. Phương trình tíchA. Lý thuyếtB. Một số dạng toán thường gặp

Bài 4. Phương trình tích

A. Lý thuyết

1. Phương trình tích và cách giải

* Phương trình tích có dạng A(x).B(x) = 0

Cách giải phương trình tích A(x).B(x) = 0 ⇔ 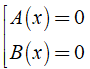Lý thuyết Toán 8: Bài 4. Phương trình tích| Giải Toán 8

* Cách bước giải phương trình tích

Bước 1: Đưa phương trình đã cho về dạng tổng quát A( x ).B( x ) = 0 bằng cách:

   + Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.

   + Phân tích đa thức ở vế phải thành nhân tử

Bước 2: Giải phương trình và kết luận

2. Ví dụ minh họa

Ví dụ 1: Giải phương trình (x + 1)(x + 4) = (2 - x)(2 + x)

Hướng dẫn:

Ta có: (x + 1)(x + 4) = (2 - x)(2 + x) ⇔ x2 + 5x + 4 = 4 - x2

⇔ 2x2 + 5x = 0 ⇔ x(2x + 5) = 0

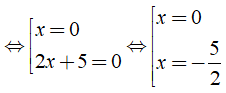
Lý thuyết Toán 8: Bài 4. Phương trình tích| Giải Toán 8

Vậy phương trình đã cho có tập nghiệm là S = {- 5/2; 0}

Ví dụ 2: Giải phương trình x3 - x2 = 1 - x

Hướng dẫn:

Ta có: x3 - x2 = 1 - x ⇔ x2(x - 1) = - (x - 1)

⇔ x2(x - 1) + (x - 1) = 0 ⇔ (x - 1)(x2 + 1) = 0

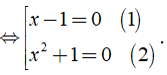
Lý thuyết Toán 8: Bài 4. Phương trình tích| Giải Toán 8

(1) ⇔ x - 1 = 0 ⇔ x = 1.

(2) ⇔ x2 + 1 = 0 (Vô nghiệm vì x2 ≥ 0 ⇒ x2 + 1 ≥ 1 )

Vậy phương trình đã cho có tập nghiệm là S = {1}.

B. Một số dạng toán thường gặp

Dạng 1: Giải phương trình tích

Phương pháp:

Ta dùng các quy tắc phá ngoặc, chuyển vế, hằng đẳng thức và phân tích đa thức thành nhân tử để biến đổi phương trình đã cho về dạng A(x).B(x)=0⇔A(x)=0 hoặc B(x)=0.

Xem thêm Giải Toán 8: Bài 4. Phương trình tích

Từ khóa » Học Toán Lớp 8 Bài 4 Phương Trình Tích