Lý Thuyết Và Bài Tập Dấu Tam Thức Bậc Hai - O2 Education

Có thể bạn quan tâm

Lý thuyết và bài tập dấu tam thức bậc hai

Sử dụng kiến thức về dấu tam thức bậc hai, chúng ta có thể giải quyết được 2 dạng toán quan trọng sau:

Tìm điều kiện để tam thức bậc hai luôn dương, luôn âm
Cách giải phương trình chứa căn, bất phương trình chứa căn

1. Tam thức bậc hai là gì?

Tam thức bậc hai đối với biến $x$ là biểu thức có dạng $$f(x) = ax^2+ bx + c,$$ trong đó $a, b, c$ là những hệ số, $a \ne 0$.

2. Định lí về dấu của tam thức bậc hai

2.1. Định lí dấu tam thức bậc hai

Cho tam thức bậc hai $ f(x)=ax^2+bx+c $ với $ a\ne 0 $ có $ \Delta=b^2-4ac $. Khi đó, có ba trường hợp xảy ra:

$ \Delta <0 $: $ f(x) $ cùng dấu với hệ số $ a $ với mọi $ x\in \mathbb{R}, $
$ \Delta =0 $: $ f(x) $ cùng dấu với hệ số $ a $ với mọi $ x\ne -\frac{b}{2a}, $
$ \Delta >0 $: $ f(x) $ có hai nghiệm phân biệt $ x_1,x_2 $ (giả sử $ x_1<x_2 $), và dấu của $ f(x) $ xác định bởi quy tắc trong trái — ngoài cùng, nghĩa là ở giữa hai số $0$ thì thì $ f(x) $ và hệ số $ a $ trái dấu, còn bên ngoài hai số $0$ thì cùng dấu.

bảng xét dấu tam thức bậc hai

2.2. Minh họa hình học của định lý dấu tam thức bậc hai

Định lí về dấu của tam thức bậc hai có minh họa hình học sau

định lí về dấu tam thức bậc hai

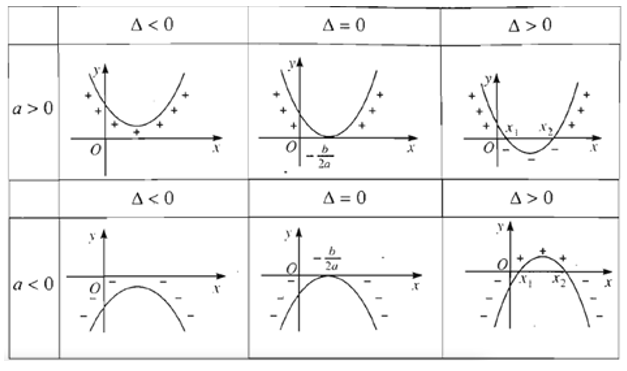
2.3. Ứng dụng định lí dấu của tam thức bậc hai

Nhận xét rằng trong cả hai trường hợp $ a>0 $ và $ a<0 $ thì

$ f(x) $ luôn có đủ hai loại dấu cả âm và dương nếu $ \Delta >0, $
$ f(x) $ chỉ có một loại dấu hoặc âm hoặc dương nếu $ \Delta \leqslant 0. $

Do đó, chúng ta có các bài toán sau đây, với $ f(x)=ax^2+bx+c $ trong đó $ a\ne 0 $:

$ f(x) >0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0\\ a>0 \end{cases}$
$ f(x) <0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0\\ a<0 \end{cases}$
$ f(x) \geqslant 0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \leqslant 0\\ a>0 \end{cases}$
$ f(x) \leqslant 0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \leqslant 0\\ a<0 \end{cases}$

Chi tiết về vấn đề này, xin mời các em học sinh xem trong bài giảng Tìm điều kiện để tam thức bậc hai luôn dương, luôn âm

2.4. Định lí đảo dấu tam thức bậc hai

Cho tam thức bậc hai $ f(x)=ax^2+bx+c $, với $ a\ne 0 $, có hai nghiệm phân biệt $ x_1<x_2 $ và một số $ \epsilon $. Khi đó, ta có các kết quả sau

$ x_1<\epsilon <x_2 \Leftrightarrow a\cdot f(\epsilon)<0$
$ \epsilon <x_1<x_2 \Leftrightarrow \begin{cases} \Delta >0\\ a\cdot f(\epsilon)>0\\ \epsilon <\frac{S}{2} \end{cases}$
$ x_1<x_2<\epsilon \Leftrightarrow \begin{cases} \Delta >0\\ a\cdot f(\epsilon)>0\\ \frac{S}{2}<\epsilon \end{cases}$

Ứng dụng của định lí đảo là dùng để so sánh một số với hai nghiệm của phương trình bậc hai. Chi tiết vấn đề này, mời các em tham khảo bài So sánh 1 số với 2 nghiệm của phương trình bậc hai

3. Bài tập về dấu tam thức bậc hai

Bài 1. Xét dấu các tam thức sau

$ f(x)=x^2-5x+6$
$ g(x)=-x^2+4x+5$
$ h(x)=6x^2+x+4$

Hướng dẫn.

Tam thức bậc hai $f(x)$ có hệ số $ a=6$ và có hai nghiệm $ x_1=2,x_2=3 $ nên có bảng xét dấu như sau:
Tam thức bậc hai $ g(x)=-x^2+4x+5$ có hệ số $ a=-1$ và có hai nghiệm $ x_1=-1,x_2=5 $ nên có bảng xét dấu như sau:
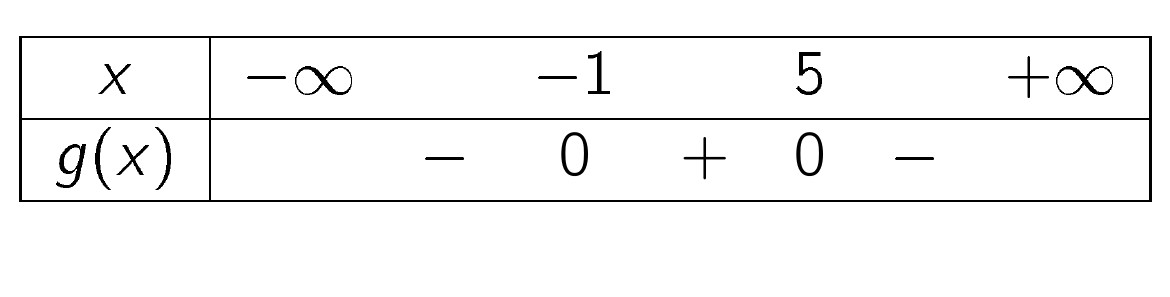
Tam thức bậc hai $ h(x)=6x^2+x+4$ có hệ số $ a=6$ và có $ \Delta <0$ nên có bảng xét dấu như sau:

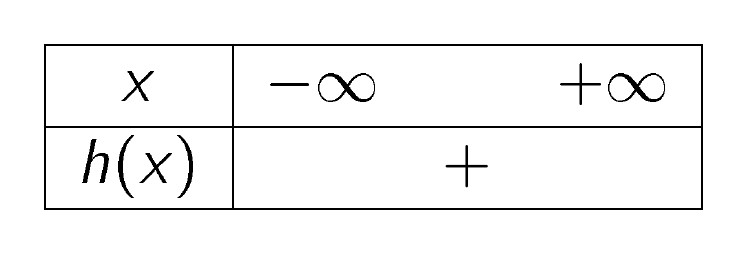
Bài 2. Giải các bất phương trình sau

$x^2-2x+3>0$
$x^2+9>6x$
$6x^2-x-2 \geqslant 0$
$\frac{1}{3}x^2+3x+6<0$
$\dfrac{x^2+1}{x^2+3x-10}<0$
$\dfrac{10-x}{5+x^2}>\dfrac{1}{2}$
$\dfrac{x+1}{x-1}+2>\dfrac{x-1}{x}$
$\dfrac{1}{x+1}+\dfrac{2}{x+3}<\dfrac{3}{x+2}$

Hướng dẫn. Để giải các bất phương trình hữu tỉ, chúng ta biến đổi (rút gọn, quy đồng giữ lại mẫu) để được một bất phương trình tích, thương các nhị thức bậc nhất và tam thức bậc hai. Sau đó lập bảng xét dấu và căn cứ vào đó để kết luận.

$x^2-2x+3>0.$ Bất phương trình này chỉ gồm một tam thức bậc hai nên chúng ta lập bảng xét dấu luôn, được kết quả như sau: 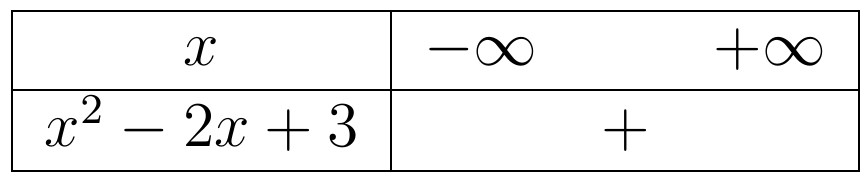Từ bảng xét dấu, chúng ta có tập nghiệm của bất phương trình là $\mathbb{R}$.
$x^2+9>6x$. Biến đổi bất phương trình đã cho thành $$x^2+9-6x>0$$ Bảng xét dấu của vế trái như sau: Suy ra, tập nghiệm của bất phương trình đã cho là $\mathbb{R}\setminus \{0\}$.
$6x^2-x-2 \geqslant 0$. Lập bảng xét dấu cho vế trái, ta được: 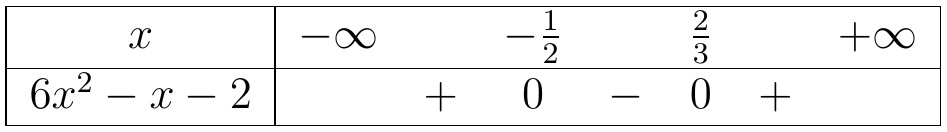Suy ra, tập nghiệm của bất phương trình đã cho là $ S=\left(-\infty;-\frac{1}{2}\right]\cup \left[\frac{2}{3};+\infty\right)$.
$\frac{1}{3}x^2+3x+6<0$. Bảng xét dấu của vế trái: 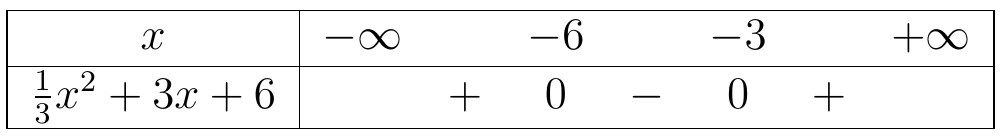Kết luận, tập nghiệm của bất phương trình là $S=(-6;-3)$.
$\dfrac{x^2+1}{x^2+3x-10}<0$. Lập bảng xét dấu cho vế trái, chúng ta có bảng sau: 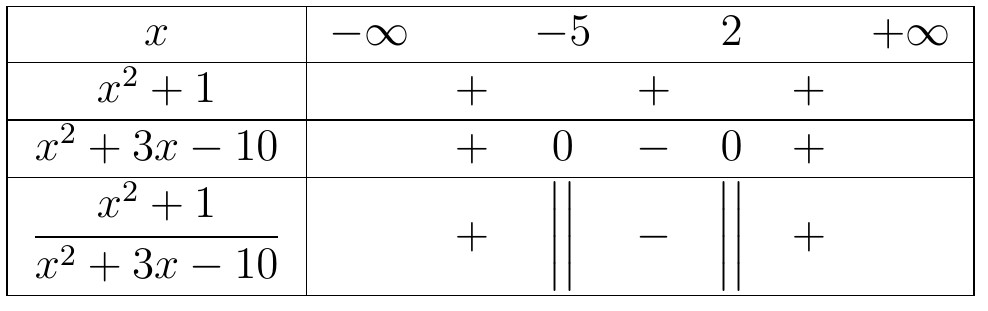Kết luận, tập nghiệm của bất phương trình là $S=(-5;2)$.
$\dfrac{10-x}{5+x^2}>\dfrac{1}{2}$. Chuyển vế, quy đồng giữ lại mẫu của bất phương trình đã cho, ta được bất phương trình tương đương $$\frac{-x^{2}-2x+15}{2\left( x^{2}+5\right) }>0$$ Lập bảng xét dấu cho vế trái bất phương trình này, ta được bảng sau:Kết luận, tập nghiệm của bất phương trình là $S=(-5;3)$.
$\dfrac{x+1}{x-1}+2>\dfrac{x-1}{x}$. Chuyển vế, quy đồng giữ mẫu của bất phương trình này, ta được bất phương trình tương đương: $$\frac{2x^{2}+x-1}{x^{2}-x}>0$$Lập bảng xét dấu cho vế trái, ta được: 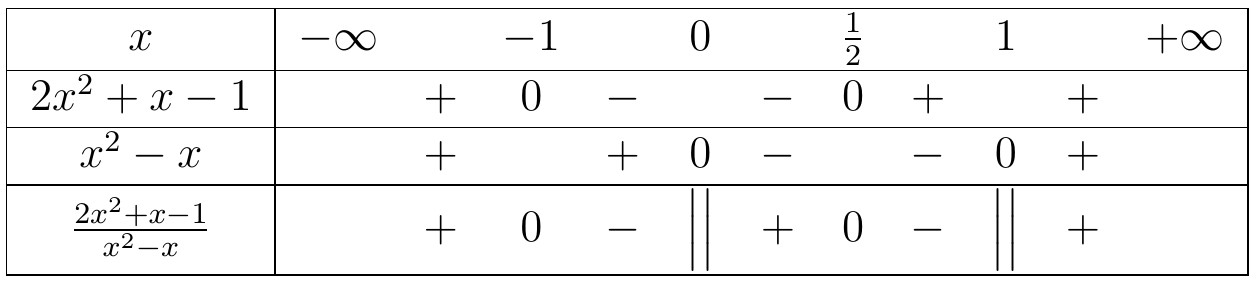Kết luận, tập nghiệm của bất phương trình đã cho là $S= \left( -\infty ,-1\right) \cup \left( 0,\frac{1}{2}\right) \cup \left( 1,+\infty \right) $.
$\dfrac{1}{x+1}+\dfrac{2}{x+3}<\dfrac{3}{x+2}$. Chuyển vế, quy đồng ta được bất phương trình tương đương: $$\frac{-x+1}{\left( x+3\right) \left( x+2\right) \left( x+1\right) }<0$$ Lập bảng xét dấu cho vế trái, ta được: 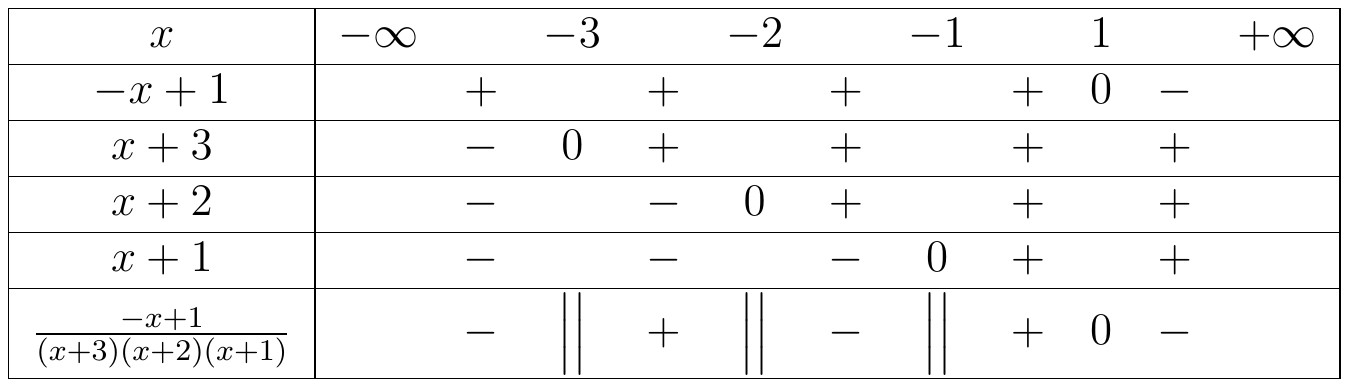Căn cứ vào bảng xét dấu, chúng ta có tập nghiệm của bất phương trình đã cho là $S=\left( -\infty ,-3\right) \cup \left( -2,-1\right) \cup \left( 1,+\infty \right) $.