Lý Thuyết Về Căn Bậc 2 – Toán Lớp 9 HOCMAI

A. Căn bậc 2 Toán lớp 9

I. Lý thuyết về căn bậc 2

1. Khái niệm

Căn bậc hai của một số a (điều kiện a không âm) là số x thì thỏa mãi điều kiện x² = a

2. Các tính chất của căn bậc 2

– Không có căn bậc 2 của số âm

– Số 0 chỉ có một căn bậc hai duy nhất đó chính là số 0, ta viết √0 = 0

– Một số dương a bất kỳ có 2 và chỉ 2 căn bậc hai là hai số đối nhau (trái dấu nhau); số dương ký hiệu là √a, số âm ký hiệu là -√a.

Vậy căn bậc 2 của a = √a và -√a

3. Ví dụ cụ thể

– Căn bậc 2 của 64 là 8 và -8.

– Căn bậc 2 cuả 10 là √10 và -√10

– Không có căn bậc 2 của -20 do -20 < 0

II. CĂN BẬC HAI SỐ HỌC

1. Định nghĩa về căn bậc hai số học

– Cho một số dương a bất kỳ thì số √a được gọi là căn bậc hai số học của a.

– TH đặc biệt: Số 0 cũng được gọi là căn bậc hai số học của 0.

– Ta viết x = √a <=> x >= 0 và x² = a

– Một số ví dụ minh họa:

• Căn bậc hai số học của 9 là √9 (= 3).
• Căn bậc hai số học của 7 là √7 (≈ 2,645751311…)

Ví dụ 1: Tìm căn bậc hai số học của các số sau đây: 100, 121, 625, 10000

Giải:

• Căn bậc hai số học của 100 là √100 (= 10).
• Căn bậc hai số học của 121 là √121 (= 11)
• Căn bậc hai số học của 625 là √625 (= 25)
• Căn bậc hai số học của 10000 là √10000 (=100)

2. Phép khai phương

– Phép khai phương là phép toán học tìm căn bậc hai số học của số không âm – lớn hơn 0 (Phép khai phương gọi tắt là khai phương).

– Khi biết một căn bậc hai số học của một số, chúng ta sẽ dễ dàng xác định được các căn bậc hai của số này.

– Ví dụ minh họa:

Căn bậc hai số học của 64 là 8 vậy 64 sẽ có hai căn bậc hai là 8 và -8.

Căn bậc hai số học cuả 10000 là 100 vậy 10000 sẽ có hai căn bậc hai là 100 và -100

Căn bậc hai số học của 121 là 11 vậy 121 sẽ có hai căn bậc hai là 11 và -11

3. Một số kết quả cần nhớ

– Với trường hợp: a ≥ 0 thì a = (√a)2.

– Với trường hợp: a ≥ 0, nếu x ≥ 0 và x2 = a thì x = √a.

– Với trường hợp: a ≥ 0 và x2 = a thì x = ±√a.

III. SO SÁNH CÁC CĂN BẬC HAI SỐ HỌC.

Định lý so sánh các căn bậc 2 số học

Cho hai số a và b đều không âm, ta có biểu thức như sau:

a > b ⇔ √a > √b

Một số ví dụ minh họa:

1. So sánh 1 với √2

Hướng dẫn giải:

Ta có 1 < 2 ⇒ √1 < √2.

Vậy 1 < √2.

2. So sánh 4 với √7.

Hướng dẫn giải:

Ta có 16 > 7 ⇒ √16 > √7

Vậy 4 > √7.

3. Hãy so sánh các số sau:

a) 4 và √17

b) 8 và √52

Hướng dẫn giải:

a) Ta có: 4 = √16 mà 17 > 16 nên √17 > √16. Vậy √17 > 4

b) Ta có: 8 = √64 mà 64 > 52 nên √64 > √52 tức 8 < √52

B. Một số dạng bài về căn bậc hai lớp 9

Dạng 1: Tìm căn bậc hai số học và so sánh hai căn bậc hai.

Phương pháp giải:

Áp dụng định lý so sánh các căn bậc 2 số học như sau:

Cho hai số a và b đều không âm, ta có biểu thức như sau:

a > b ⇔ √a > √b

Dạng 2: Tính giá trị của biểu thức chứa căn bậc hai

Phương pháp giải:

Sử dụng hằng đẳng thức

√A² = |A| = A (Khi A >= 0) và – A (Khi A < 0)

Dạng 3: Rút gọn biểu thức chứa căn

Phương pháp giải:

Đưa các biểu thức chứa căn về dạng hằng đẳng thức đáng nhớ. Một số hằng đẳng thức hay sử dụng trong dạng này gồm:

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• √A² = A (khi A >= 0) và -A (khi A < 0)

Dạng 4: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa

Phương pháp giải:

Sử dụng định lý √A có nghĩa ⇔ A >= 0

Dạng 5: Giải phương trình chưa căn bậc 2

Phương pháp giải:

Các em học sinh cần lưu ý một số phép biến đổi tương đương có liên quan đến căn bậc 2 như sau:

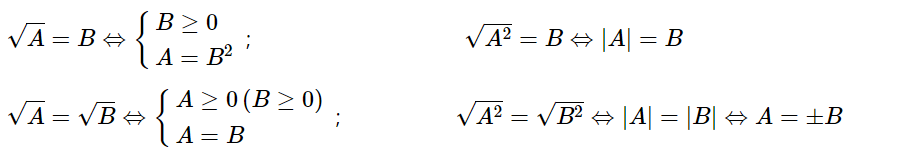HM10 2024 - GIẢI PHÁP LUYỆN THI TOÀN DIỆN NẮM CHẮC KIẾN THỨC - KHÔNG LO BIẾN DỘNG ĐỀ THI

• Lộ trình toàn diện - NẮM CHẮC NỀN TẢNG - TỔNG ÔN TOÀN DIỆN - LUYỆN ĐỀ CHUYÊN SÂU
• ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP VỚI MỌI NHU CẦU
• TOP THẦY CÔ DANH TIẾNG, GIÀU KINH NGHIỆM
• DỊCH VỤ HỖ TRỢ HỌC TẬP ĐÔNG HÀNH TRONG SUÔT QUÁ TRÌNH HỌC TẬP

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này! HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY TOPCLASS 2024 - CHƯƠNG TRÌNH HỌC TOÀN DIỆN NẮM CHẮC KIẾN THỨC - BỨT PHÁ ĐIỂM SỐ

• Chu trình học tập khép kín HỌC - LUYỆN - HỎI - KIỂM TRA
• Đa dạng hình thức học - Phù hợp với mọi nhu cầu
• Đội ngũ giáo viên giảng dạy nổi tiếng với 16+ năm kinh nghiệm
• Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này! HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

Tham khảo ngay: Tài liệu ôn tập Toán lớp 9

C Bài tập thực hành căn bậc 2 lớp 9

Bài 1: Tìm x để các căn thức bậc hai sau có nghĩa

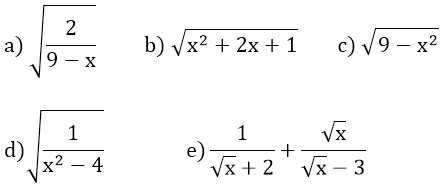
Bài 2: Rút gọn các biểu thức sau:

Bài 3: Giải các phương trình sau:

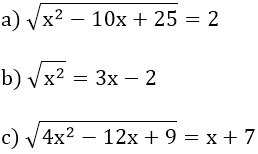
Bài 4: Chứng minh rằng:

√2 + √6 + √12 + √20 + √30 + √42 < 24

Bài 5: Tìm giá trị lớn nhất của biểu thức:

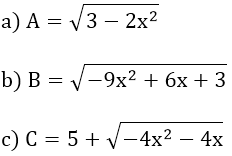
Bài 6: Rút gọn biểu thức A

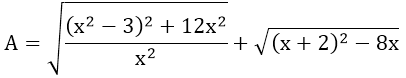
Bài 7: Cho biểu thức M có dạng:

a) Rút gọn biểu thức M;

b) Tìm các giá trị của x để M = 4.

Bài 8: Tìm giá trị nhỏ nhất của mỗi biểu thức:

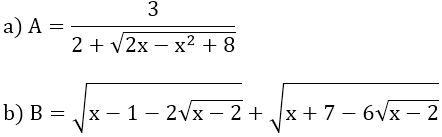
Bài 9: Tìm x, để

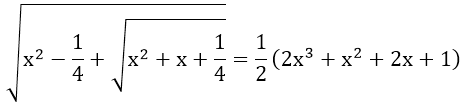
Trên đây là toàn bộ kiến thức mà các em học sinh cần nắm được về Căn bậc 2 trong chương trình Toán lớp 9. Hy vọng bài viết trên sẽ giúp các em có thêm kiến thức để giải các dạng bài tập liên quan tới căn bậc 2 lớp 9.

RELATED ARTICLESMORE FROM AUTHOR

TỔNG HỢP CÁC MÔN THI VÀO 10 CỦA CÁC TỈNH,THÀNH TRÊN CẢ NƯỚC – NĂM HỌC 2025

Khoe điểm học kỳ I – Nhận ngay những phần quà hấp dẫn từ HOCMAI!

ĐỒNG HÀNH CÙNG PH/HS 2010 CHINH PHỤC KỲ THI VÀO 10 TẠI HÀ NỘI NĂM HỌC 2024-2025 CÙNG HOCMAI & TRƯỜNG H.A.S