Lý Thuyết Về Căn Thức Bậc Hai Và Hằng đẳng Thức √A^2

Trang chủ » Căn Của 2a^2 » Lý Thuyết Về Căn Thức Bậc Hai Và Hằng đẳng Thức √A^2

Có thể bạn quan tâm

1. Căn thức bậc hai

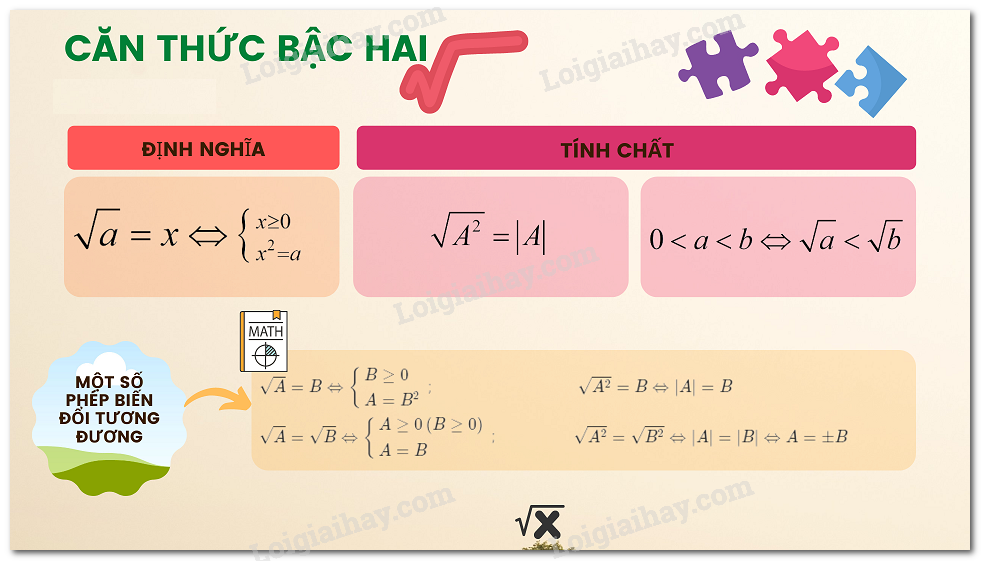
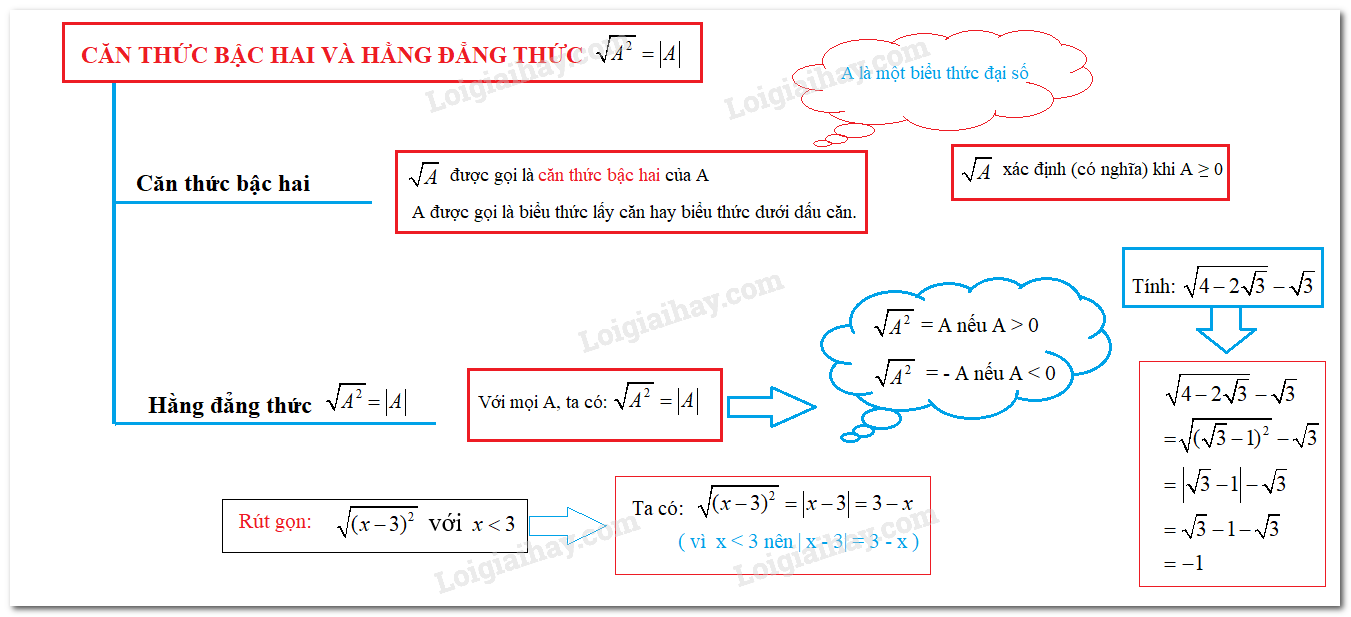
Với \(A\) là một biểu thức đại số, người ta gọi \(\sqrt A \) là căn thức bậc hai của \(A\). Khi đó, \(A\) được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.

\(\sqrt A \) xác định hay có nghĩa khi \(A\) lấy giá trị không âm.

2. Hằng đẳng thức \(\sqrt {{A^2}}  = \left| A \right|\)  

Với mọi số \(a\), ta có \(\sqrt {{a^2}}  = \left| a \right|\).

* Một cách tổng quát, với \(A\) là một biểu thức ta có 

\(\sqrt {{A^2}}  = \left| A \right|\) nghĩa là 

\(\sqrt {{A^2}}  = A\) nếu \(A \ge 0\) và \(\sqrt {{A^2}}  =  - A\) nếu \(A < 0\).

3. Các dạng toán cơ bản

Dạng 1: Tìm điều kiện để căn thức xác định

Ta có \(\sqrt A \) xác định hay có nghĩa khi \(A\ge 0\) 

Ví dụ: \(\sqrt {x - 1} \) xác định khi \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)

Dạng 2: Rút gọn biểu thức 

Sử dụng:  Với \(A\) là một biểu thức ta có \(\sqrt {{A^2}}  = \left| A \right|\)

Vì dụ: Với \(x>2\) ta có: \(A = \dfrac{{\sqrt {{x^2} - 4x + 4} }}{{x - 2}}\)\( = \dfrac{{\sqrt {{{\left( {x - 2} \right)}^2}} }}{{x - 2}} = \dfrac{{\left| {x - 2} \right|}}{{x - 2}} \)\(= \dfrac{{x - 2}}{{x - 2}} = 1\)

Từ khóa » Căn Của 2a^2