Ma Trận Nghịch đảo Là Gì? - Cẩm Nang Điện Máy
Có thể bạn quan tâm
Ma trận nghịch đảo là một thuật ngữ phổ biến trong đại số tuyến tính. Phép nghịch đảo thường được dùng để đơn giản hóa các phép toán ma trận phức tạp. Vậy phép nghịch đảo trong đại số tuyến tình sẽ như thế nào? Bài viết này sẽ cung cấp cụ thể ma trận nghịch đảo là gì, cách tính ma trận nghịch đảo. Đừng bỏ qua!
Contents
- 1 Ma trận nghịch đảo là gì?
- 1.1 Ma trận đơn vị, ma trận vuông
- 1.2 Ma trận khả đảo là gì?
- 1.3 Tính chất
- 1.4 Hệ quả
- 2 Tìm ma trận nghịch đảo
- 2.1 Định thức con, phần bù đại số
- 2.2 Công thức tính ma trận nghịch đảo
- 3 Tính ma trận nghịch đảo bằng thuật toán Gauss-Jordan
- 4 Cách tính ma trận nghịch đảo bằng máy tính Casio Fx570ES Plus
Ma trận nghịch đảo là gì?
Khái niệm ma trận nghịch đảo gắn liền với thuật ngữ về ma trận đơn vị, ma trận vuông và ma trận khả đảo. Vì vậy, ta cần hiểu rõ về các khái niệm này trước tiên.
Ma trận đơn vị, ma trận vuông
– Ma trận vuông là ma trận có cùng số hàng và số cột (số đơn vị ở hàng bằng số đơn vị ở cột).
Ví dụ:
1 2 3
4 5 6
7 8 9
(số phần tử ở mỗi hàng và số phần tử ở mỗi cột đều bằng 3).
Một ma trận n x n được còn thường được gọi là ma trận vuông bậc n. Hai ma trận vuông có cùng một bậc bất kỳ nào cũng có thể được cộng và nhân với nhau.
– Ma trận đơn vị cấp n là một ma trận vuông cấp n, trong đó, tất cả các phần tử nằm trên đường chéo chính bằng 1, các phần từ nằm ngoài đường chéo chính bằng 0.
Ví dụ: ta có ma trận đơn vị cấp 3 (I3) như sau:
1 0 0 0 1 0 0 0 1
Dạng tổng quát: Ma trận đơn vị In
1 0 0 … 0 0 1 0 … 0 ……………… 0 0 0 … 1
Ma trận khả đảo là gì?

Theo Wikipedia: “Ma trận khả đảo hay còn được gọi là ma trận khả nghịch / ma trận không suy biến (Invertible matrix). “Trong đại số tuyến tính, một ma trận khả nghịch là một ma trận vuông và có ma trận nghịch đảo trong phép nhân ma trận.”
Cụ thể: Một ma trận A vuông cấp n được gọi là khả nghịch nếu tồn tại ma trận A’ cùng cấp n sao cho A A’ = A’ A = I. Khi đó A’ được gọi là ma trận nghịch đảo của ma trận A đã cho, ký hiệu là A−1.
Như vật thì: A.A-1= A-1.A= In
Tính chất
1. Nếu A, B là khả nghịch thì ma trận tích AB cũng là một ma trận khả nghịch và (AB)-1= B-1. A-1
2. Nếu A khả nghịch thì ma trận chuyển vị AT cũng khả nghịch, khi đó (AT)-1= (A-1)T
Hệ quả
Gọi A là ma trận vuông cấp n trên K (n ≥ 2), khi đó, các khẳng định sau đây là đúng:
1. Ma trận A khả nghịch
2. Ma trận đơn vị In nhận được từ A bởi một số hữu hạn các phép biến đổi sơ cấp dòng (cột)
3. Ma trận A là tích của một số hữu hạn các ma trận sơ cấp
Tìm ma trận nghịch đảo

Định thức con, phần bù đại số
Ta có một ma trận vuông A cấp n và phần tử aij. Định thức của ma trận cấp n-1 lấy từ A bằng cách xóa đi dòng thứ i, cột thứ j thì được gọi là định thức con của A ứng với phần tử aij, ký hiệu là Mij.
Định thức Mij với dấu bằng (-1)i+j được gọi là phần bù đại số của phần tử aij, ký hiệu Aij.

Công thức tính ma trận nghịch đảo
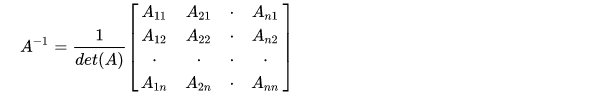
- Bước 1: Tính định thức của ma trận A đã cho Nếu det (A) = 0 thì kết luận A không có ma trận nghịch đảo A-1 Ngược lại, nếu det (A) ≠ 0 thì A có ma trận nghịch đảo A-1 (ma trận A khả đảo)
- Bước 2: Lập ma trận chuyển vị A’ của ma trận A đã cho
- Bước 3: Lập ma trận phụ hợp của ma trận A Trong đó: A* = (A’ij)nm Với A’ = (A’ij) là phần bù đại số của phần tử ở hàng i, cột j trong ma trận chuyển vị A’
- Bước 4: Tính ma trận A-1
Ví dụ:

Tính ma trận nghịch đảo bằng thuật toán Gauss-Jordan
Sử dụng phép khử Gauss-Jordan để tính ma trận nghịch đảo là phương pháp áp dụng hệ quả (số 2) của ma trận khả đảo. Cách làm cụ thể như sau:
Bước 1: lập ma trận A | In có n hàng, 2n cột bằng cách ghép thêm ma trận đơn vị cấp n vào bên cạnh ma trận A
Bước 2: Sử dụng các phép biến đổi sơ cấp dòng để đưa ma trận [ A|I ] về dạng [ A’ | B ], với A’ là một ma trận bậc thang chính tắc thu được qua phép khử Gauss.
Bước 3: Kết luận
- Nếu A’ = In thì A khả đảo và A-1 = B
- Nếu A’ ≠ In thì ma trận A không khả đảo. Chỉ cần trong quá trình biến đổi nếu A’ xuất hiện ít nhất 1 dòng 0 thì lập tức kết luận A không khả đảo. Như vậy sẽ không cần phải đưa A’ về dạng chính tắc và kết thúc thuật toán.
Ví dụ: Sử dụng phép khử Gauss – Jordan để tìm ma trận nghịch đảo của ma trận A sau và từ đó tính ra A2008.
Cách tính ma trận nghịch đảo bằng máy tính Casio Fx570ES Plus
Sử dụng máy tính cầm tay để tính toán hoặc kiểm tra kết quả tìm ma trận nghịch đảo giúp ta tránh khỏi các sai sót. Sau đây là hướng dẫn bấm máy ma trận nghịch đảo nên tham khảo:

Mong rằng các nội dung trên đây sẽ giúp các bạn nắm rõ và giải quyết tốt các bài toán về ma trận nghịch đảo. Đừng quên ghé thăm camnangdienmay.net để cập nhật nhiều kiến thức toán học nói riêng và nhiều chủ đề thiết thực khác!
Từ khóa » Tính Ma Trận Nghịch đảo Bậc 2
-
Ma Trận Nghịch đảo Là Gì? Cách Tính Bằng Tay Và Máy Tính - VOH
-
Cách Tính Ma Trận Nghịch Đảo Cấp 2, Ma Trận Khả Nghịch
-
Cách Tìm Ma Trận Nghịch đảo 2x2, 3x3, 4x4 Chính Xác 100%
-
Ma Trận Nghịch đảo Là Gì? Cách Tìm Ma Trận Nghịch đảo 2×2, 3×3, 4×4
-
Cách để Tìm Nghịch đảo Của Ma Trận 3x3 - WikiHow
-
[CHUẨN NHẤT] Cách Tìm Ma Trận Nghịch đảo 2x2 - TopLoigiai
-
Ma Trận Khả Nghịch – Wikipedia Tiếng Việt
-
27) Toán 2 - Tìm Ma Trận Nghịch đảo (Phần 1)
-
- Ma Trận Nghịch đảo - Thầy: Đặng Thành Nam - YouTube
-
Video Cách Tính Ma Trận Nghịch đảo - Mitadoor Đồng Nai
-
Ma Trận Nghịch Đảo 2X2 - Cách Tính Bằng Tay Và Máy Tính
-
Ma Trận Nghịch đảo Là Gì?
-
Tinh Toán Ma Trận