Home > Forums > Software User Forums > OpenFOAM > OpenFOAM Programming & Development
 February 28, 2012, 11:51 February 28, 2012, 11:51 |  Meaning of "fvc::div(phi)" Meaning of "fvc::div(phi)" | #1 |
enoch Member Jeong Kim Join Date: Feb 2010 Posts: 42 Rep Power: 17  | Hi Foamers, When I look at pEqn.C in the "twoPhaseEulerFoam" solver, I don't really understand the following codes. ....... for(int nonOrth=0; nonOrth<=nNonOrthCorr; nonOrth++) { fvScalarMatrix pEqn ( fvm::laplacian(Dp, p) == fvc::div(phi) ); ..... Speaking of div(phi), divergence of any scalar is zero mathematically. Divergence reduce the order rank of maxtrix. For an example, let's say, velcotiy vector u=(ux, uy) div(u)=ux/dx + uy/dy ---> scalar quantity But, scalar phi=phi(x,y) div(phi)=0 So what is the meaning of div(phi) and what's a mathematical formulation for the term in openfoam? Zhiheng Wang, qwebean and nepomnyi like this. |
 |  |
 July 16, 2013, 05:01 July 16, 2013, 05:01 |  | #2 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Hi Kim, This problem happens to me in the same time!http://www.cfd-online.com/Forums/ope...-equation.html Did you find a solution? Zhiheng Wang likes this. |
 |  |
 July 16, 2013, 07:01 July 16, 2013, 07:01 |  | #3 |
fportela Member Felipe Alves Portela Join Date: Dec 2012 Location: FR Posts: 70 Rep Power: 15  | Isn't phi simply the mass flux rho*U*A ? check this HTML Code: http://openfoamwiki.net/index.php/Uguide_table_of_fields and this HTML Code: http://openfoamwiki.net/index.php/Main_FAQ#What_is_the_field_phi_that_the_solver_is_writing I have not used this particular solver, so I'm not sure what's going on, but from continuity: div(phi) = 0 implies that ddt(rho) is zero, if this is not the case, then div(phi) is not zero. Cheers, Felipe elmo555 likes this. |
 |  |
 July 16, 2013, 09:31 July 16, 2013, 09:31 |  | #4 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Hi Felipre, Thanks for your prompt reply, Quote: Originally Posted by fportela 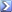 but from continuity: div(phi) = 0 but from continuity: div(phi) = 0 | regarding this, isnt it should be div(u)=0? Zhiheng Wang likes this. |
 |  |
 July 16, 2013, 09:35 July 16, 2013, 09:35 |  | #5 |
Bernhard Senior Member Bernhard Join Date: Sep 2009 Location: Delft Posts: 790 Rep Power: 23  | No, because U is the cell centre value, and the divergence is obtained from the face values, i.e. phi. fportela, utkunun, randolph and 1 others like this. |
 |  |
 July 16, 2013, 09:38 July 16, 2013, 09:38 |  | #6 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Hi Bernhard, Could you explain more? Zhiheng Wang likes this. |
 |  |
 July 16, 2013, 09:39 July 16, 2013, 09:39 |  | #7 |
Bernhard Senior Member Bernhard Join Date: Sep 2009 Location: Delft Posts: 790 Rep Power: 23  | Can you be more specific? Zhiheng Wang likes this. |
 |  |
 July 16, 2013, 09:44 July 16, 2013, 09:44 |  | #8 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Quote: Originally Posted by Bernhard 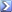 No, because U is the cell centre value, and the divergence is obtained from the face values, i.e. phi. No, because U is the cell centre value, and the divergence is obtained from the face values, i.e. phi. | I mean all the books say from continuity we have:  without mentioning whether its cell centre value or the face value. But Im sure I confused about this. So? without mentioning whether its cell centre value or the face value. But Im sure I confused about this. So? |
 |  |
 July 16, 2013, 09:49 July 16, 2013, 09:49 | 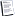 | #9 |
Bernhard Senior Member Bernhard Join Date: Sep 2009 Location: Delft Posts: 790 Rep Power: 23  | The book are correct, but  is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). Kummi, SHUBHAM9595 and fly_light like this. is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). Kummi, SHUBHAM9595 and fly_light like this. |
 |  |
 July 16, 2013, 09:51 July 16, 2013, 09:51 | 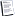 | #10 |
fportela Member Felipe Alves Portela Join Date: Dec 2012 Location: FR Posts: 70 Rep Power: 15  | Quote: Originally Posted by sharonyue  I mean all the books say from continuity we have: I mean all the books say from continuity we have:  without mentioning weather its cell centre value or the face value. But Im sure I confused about this. So? without mentioning weather its cell centre value or the face value. But Im sure I confused about this. So? | This is only true for incompressible flow. For incompressible flow, you have  Plug this into continuity Plug this into continuity  And you get And you get  |
 |  |
 July 16, 2013, 10:24 July 16, 2013, 10:24 |  | #11 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Quote: Originally Posted by Bernhard  The book are correct, but The book are correct, but  is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). |  I know this, but phi is a scalar, what is div(scalar)..... Felipe. Yeah, you are right~ I know this, but phi is a scalar, what is div(scalar)..... Felipe. Yeah, you are right~ |
 |  |
 July 16, 2013, 10:27 July 16, 2013, 10:27 |  | #12 |
Bernhard Senior Member Bernhard Join Date: Sep 2009 Location: Delft Posts: 790 Rep Power: 23  | Quote: Originally Posted by sharonyue 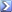 I know this, but phi is a scalar, what is div(scalar)..... I know this, but phi is a scalar, what is div(scalar)..... | Be careful here. phi is a surfaceScalarField, so there is always a direction vector defined by the face area vector. fportela and wind_ like this. |
 |  |
 July 16, 2013, 10:56 July 16, 2013, 10:56 | 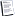 | #13 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  |  Regarding this, if div(phi)=0 Do you mean: Regarding this, if div(phi)=0 Do you mean:  Quote: Quote: | phi is a surfaceScalarField, so there is always a direction vector defined by the face area vector | Is there any difference between "surfaceScalarField" and "volScaklaField" expect where they are stored? flowAlways likes this. |
 |  |
 July 16, 2013, 11:01 July 16, 2013, 11:01 | 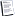 | #14 |
Bernhard Senior Member Bernhard Join Date: Sep 2009 Location: Delft Posts: 790 Rep Power: 23  | You apply the divergence theorem.  You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. fportela, flowAlways, acs and 1 others like this. You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. fportela, flowAlways, acs and 1 others like this. |
 |  |
 July 16, 2013, 11:23 July 16, 2013, 11:23 | 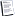 | #15 |
sharonyue Senior Member Dongyue Li Join Date: Jun 2012 Location: Beijing, China Posts: 866 Rep Power: 19  | Quote: Originally Posted by Bernhard 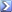 You apply the divergence theorem. You apply the divergence theorem.  You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. | Bernhard, Thanks very very much for your consistent help, But I still cannot understand this "div(u)=0" turns into "div(phi)=0" in OpenFOAM, even mathematicly div(vector) works but div(scalar) not. Does it mean fvc::div(phi)=0 equals to sum(phi)=0 in OpenFOAM? Why doesnt it use sum(phi)=0 instead. At last,I think I need to clear my head. Thanks for you patience. Really thankful. acs likes this. acs likes this. |
 |  |
 61Likes
61Likes 















 without mentioning whether its cell centre value or the face value. But Im sure I confused about this. So?
without mentioning whether its cell centre value or the face value. But Im sure I confused about this. So? 

 is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). Kummi, SHUBHAM9595 and fly_light like this.
is valid without a mesh. If you integrate this equation over a control volume, this converts to a summation over the faces of the velocity times the area ( http://en.wikipedia.org/wiki/Divergence_theorem ). phi is nothing less then the velocity at the face (times the density and the face area). Kummi, SHUBHAM9595 and fly_light like this. 

 Plug this into continuity
Plug this into continuity  And you get
And you get 


 I know this, but phi is a scalar, what is div(scalar)..... Felipe. Yeah, you are right~
I know this, but phi is a scalar, what is div(scalar)..... Felipe. Yeah, you are right~ 



 Regarding this, if div(phi)=0 Do you mean:
Regarding this, if div(phi)=0 Do you mean:  Quote:
Quote: 

 You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. fportela, flowAlways, acs and 1 others like this.
You can't integrate face values over a volume as you are posting. The difference between a volScalarField and a surfaceScalarField, is that for a volScalarField, there is a value stored per control volume or cell. For a surfaceScalarField there is a value stored per face. You can of course interpolate from the one to the other, but this is only accurate to some order. fportela, flowAlways, acs and 1 others like this. 

 acs likes this.
acs likes this. 

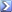 but from continuity: div(phi) = 0
but from continuity: div(phi) = 0