Mở Rộng Trong Một Chuỗi Taylor. Chuỗi Lũy Thừa, Sự Hội Tụ Của Chúng ...

Trong số các chuỗi chức năng, vị trí quan trọng nhất bị chiếm bởi các chuỗi quyền lực.

Một chuỗi lũy thừa được gọi là một chuỗi

các thành viên của nó là các hàm lũy thừa được sắp xếp theo lũy thừa số nguyên không âm tăng dần x, một c0 , c 1 , c 2 , c N là các giá trị không đổi. Con số c1 , c 2 , c N - hệ số của các thành viên trong chuỗi, c0 - thành viên miễn phí. Các số hạng của chuỗi lũy thừa được xác định trên toàn bộ dãy số.

Hãy làm quen với khái niệm vùng hội tụ của chuỗi lũy thừa. Đây là tập hợp các giá trị biến x mà chuỗi hội tụ. Chuỗi lũy thừa có một vùng hội tụ khá đơn giản. Đối với các giá trị thực của một biến x khu vực hội tụ bao gồm một điểm duy nhất hoặc là một khoảng nhất định (khoảng hội tụ), hoặc trùng với toàn bộ trục Con bò .

Khi thay thế trong một chuỗi lũy thừa, các giá trị x= 0 bạn nhận được một chuỗi số

c0 +0+0+...+0+... ,

cái nào hội tụ.

Do đó, tại x= 0 hội tụ bất kỳ chuỗi lũy thừa nào và do đó, khu vực hội tụ của nó không thể là một tập hợp trống. Cấu trúc của vùng hội tụ của tất cả các chuỗi lũy thừa là như nhau. Nó có thể được thiết lập bằng cách sử dụng định lý sau.

Định lý 1 (Định lý Abel). Nếu chuỗi lũy thừa hội tụ tại một số giá trị x = x 0 , khác 0, thì nó hội tụ, và hơn nữa, hoàn toàn, đối với tất cả các giá trị |x| < |x 0 | . Xin lưu ý: cả giá trị bắt đầu "x bằng 0" và bất kỳ giá trị nào của "x" được so sánh với giá trị bắt đầu đều được tính theo modulo - mà không tính đến dấu hiệu.

Hậu quả. Nếu một phân kỳ chuỗi điện ở một số giá trị x = x 1 , sau đó nó phân kỳ cho tất cả các giá trị |x| > |x 1 | .

Như chúng ta đã tìm hiểu trước đó, bất kỳ chuỗi lũy thừa nào đều hội tụ cho giá trị x= 0. Có chuỗi lũy thừa chỉ hội tụ cho x= 0 và phân kỳ cho các giá trị khác X. Loại trừ trường hợp này khỏi việc xem xét, chúng tôi giả định rằng chuỗi lũy thừa hội tụ tại một số giá trị x = x 0 , khác 0. Khi đó, theo định lý Abel, nó hội tụ tại mọi điểm trong khoảng] - | x0 |, |x 0 |[ (khoảng, ranh giới bên trái và bên phải của chúng là các giá trị của x, tại đó chuỗi lũy thừa hội tụ, lấy tương ứng với một dấu trừ và một dấu cộng), đối xứng về gốc.

Nếu chuỗi công suất phân kỳ ở một số giá trị x = x 1 , sau đó, dựa trên hệ quả của định lý Abel, nó cũng phân kỳ tại tất cả các điểm bên ngoài đoạn [- | x1 |, |x 1 |] . Theo đó, đối với bất kỳ chuỗi lũy thừa nào thì có một khoảng, đối xứng với gốc, được gọi là khoảng hội tụ , tại mỗi điểm mà chuỗi hội tụ, có thể hội tụ tại các ranh giới, hoặc có thể phân kỳ, và không nhất thiết đồng thời, nhưng bên ngoài phân đoạn, chuỗi phân kỳ. Con số Rđược gọi là bán kính hội tụ của chuỗi lũy thừa.

Trong những trường hợp đặc biệt khoảng thời gian hội tụ chuỗi công suất có thể suy biến đến một điểm (khi đó chuỗi chỉ hội tụ cho x= 0 và giả định rằng R= 0) hoặc đại diện cho toàn bộ trục số (khi đó dãy số hội tụ tại tất cả các điểm của trục số và giả sử như vậy).

Do đó, định nghĩa vùng hội tụ của một chuỗi lũy thừa là xác định bán kính hội tụ R và nghiên cứu về sự hội tụ của chuỗi trên các ranh giới của khoảng hội tụ (cho).

Định lý 2. Nếu tất cả các hệ số của chuỗi lũy thừa, bắt đầu từ một chuỗi nào đó, đều khác không, thì bán kính hội tụ của nó bằng giới hạn theo tỷ lệ giữa các giá trị tuyệt đối của hệ số của các phần tử chung sau của chuỗi, tức là

Ví dụ 1. Tìm miền hội tụ của một chuỗi lũy thừa

Quyết định. Đây

Sử dụng công thức (28), chúng tôi tìm thấy bán kính hội tụ của chuỗi này:

Chúng ta hãy nghiên cứu sự hội tụ của chuỗi tại các điểm cuối của khoảng hội tụ. Ví dụ 13 cho thấy rằng chuỗi này hội tụ cho x= 1 và phân kỳ ở x= -1. Do đó, vùng hội tụ là nửa khoảng.

Ví dụ 2. Tìm miền hội tụ của một chuỗi lũy thừa

Quyết định. Các hệ số của chuỗi là số dương, và

Hãy để chúng tôi tìm giới hạn của tỷ lệ này, tức là bán kính hội tụ chuỗi công suất:

Chúng tôi khảo sát sự hội tụ của chuỗi ở các điểm cuối của khoảng. Thay thế giá trị x= -1/5 và x= 1/5 trong chuỗi này cho:

Đầu tiên của chuỗi này hội tụ (xem ví dụ 5). Nhưng sau đó, theo định lý của đoạn "Hội tụ tuyệt đối", chuỗi thứ hai cũng hội tụ, và vùng hội tụ của nó là đoạn

Ví dụ 3. Tìm miền hội tụ của một chuỗi lũy thừa

Quyết định. Đây

Sử dụng công thức (28), chúng tôi tìm thấy bán kính hội tụ của chuỗi:

Chúng ta hãy nghiên cứu sự hội tụ của chuỗi cho các giá trị. Thay thế chúng trong loạt bài này, tương ứng, chúng ta nhận được

Cả hai chuỗi phân kỳ bởi vì điều kiện hội tụ cần thiết không được thỏa mãn (các số hạng chung của chúng không có xu hướng bằng không). Vì vậy, ở cả hai đầu của khoảng hội tụ, chuỗi này phân kỳ và vùng hội tụ của nó là khoảng.

Ví dụ 5. Tìm miền hội tụ của một chuỗi lũy thừa

Quyết định. Chúng tôi tìm thấy mối liên hệ, ở đâu và :

Theo công thức (28), bán kính hội tụ của chuỗi này

,

nghĩa là, chuỗi chỉ hội tụ khi x= 0 và phân kỳ cho các giá trị khác X.

Các ví dụ cho thấy rằng chuỗi hoạt động khác nhau ở các đầu của khoảng hội tụ. Trong ví dụ 1, chuỗi hội tụ ở một đầu của khoảng hội tụ và phân kỳ ở điểm kia, trong ví dụ 2, chuỗi hội tụ ở cả hai đầu, trong ví dụ 3, chuỗi hội tụ ở cả hai đầu.

Công thức về bán kính hội tụ của một chuỗi lũy thừa thu được theo giả thiết rằng tất cả các hệ số của các số hạng của chuỗi, bắt đầu từ một số, là khác không. Do đó, chỉ cho phép áp dụng công thức (28) trong những trường hợp này. Nếu điều kiện này bị vi phạm, thì bán kính hội tụ của chuỗi lũy thừa nên được tìm kiếm bằng cách sử dụng dấu hiệu của d'Alembert hoặc, bằng cách thay đổi một biến, bằng cách biến đổi chuỗi thành dạng thỏa mãn điều kiện đã chỉ định.

Ví dụ 6. Tìm khoảng hội tụ của một chuỗi lũy thừa

Quyết định. Loạt bài này không chứa các thuật ngữ có độ lẻ X. Do đó, chúng tôi biến đổi chuỗi bằng cách thiết lập. Sau đó, chúng tôi nhận được loạt

công thức (28) có thể được sử dụng để tìm bán kính hội tụ của nó. Kể từ, và, khi đó bán kính hội tụ của chuỗi này

Do đó, từ đẳng thức chúng ta thu được, chuỗi này hội tụ trên khoảng.

Tổng chuỗi lũy thừa. Sự khác biệt và tích hợp của chuỗi nguồn

Hãy để cho một chuỗi quyền lực

bán kính hội tụ R> 0, tức là chuỗi này hội tụ trên khoảng.

Sau đó, mỗi giá trị X từ khoảng hội tụ tương ứng với một số tổng của chuỗi. Do đó, tổng của chuỗi lũy thừa là một hàm của X trên khoảng hội tụ. Biểu thị nó qua f(x), chúng ta có thể viết đẳng thức

hiểu nó theo nghĩa là tổng của chuỗi tại mỗi điểm X từ khoảng đồng biến bằng giá trị của hàm số f(x) tại thời điểm này. Theo nghĩa tương tự, chúng ta sẽ nói rằng chuỗi lũy thừa (29) hội tụ đến hàm f(x) trên khoảng hội tụ.

Bên ngoài khoảng hội tụ, đẳng thức (30) không có ý nghĩa gì.

Ví dụ 7 Tìm tổng của chuỗi lũy thừa

Quyết định. Đây là một loạt hình học một= 1 và q= x. Do đó, tổng của nó là một hàm . Chuỗi hội tụ nếu, và là khoảng hội tụ của nó. Do đó, bình đẳng

chỉ hợp lệ cho các giá trị, mặc dù hàm được xác định cho tất cả các giá trị X, Ngoài ra X= 1.

Có thể chứng minh rằng tổng của chuỗi lũy thừa f(x) là liên tục và có thể phân biệt trên bất kỳ khoảng nào trong khoảng hội tụ, cụ thể là tại bất kỳ điểm nào trong khoảng hội tụ của chuỗi.

Chúng ta hãy trình bày các định lý về sự phân biệt theo từng số hạng và tích phân của chuỗi lũy thừa.

Định lý 1. Chuỗi lũy thừa (30) trong khoảng thời gian hội tụ của nó có thể được phân biệt theo số hạng với số lần không giới hạn và chuỗi lũy thừa thu được có cùng bán kính hội tụ như chuỗi ban đầu và tổng của chúng tương ứng bằng.

Định lý 2. Chuỗi lũy thừa (30) có thể được tích hợp theo thời hạn không giới hạn số lần trong phạm vi từ 0 đến X, nếu, và chuỗi lũy thừa có cùng bán kính hội tụ với chuỗi ban đầu, và tổng của chúng tương ứng bằng

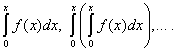
Mở rộng các chức năng thành chuỗi công suất

Để chức năng f(x), sẽ được mở rộng thành một chuỗi lũy thừa, tức là biểu diễn ở dạng (30):

Vấn đề là xác định các hệ số hàng (30). Để làm điều này, phân biệt các số hạng bình đẳng (30) theo số hạng, chúng tôi tuần tự tìm thấy:

……………………………………………….. (31)

Giả sử bằng nhau (30) và (31) X= 0, chúng tôi tìm thấy

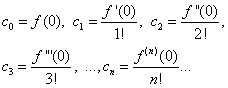
Thay các biểu thức tìm được vào đẳng thức (30), chúng ta thu được

(32)

Hãy để chúng tôi tìm sự mở rộng chuỗi Maclaurin của một số hàm cơ bản.

Ví dụ 8 Mở rộng chức năng trong chuỗi Maclaurin

Quyết định. Các đạo hàm của hàm này giống như chính hàm:

Do đó, khi X= 0 chúng tôi có

Thay các giá trị này vào công thức (32), chúng ta sẽ có được sự mở rộng mong muốn:

(33)

Dãy số này hội tụ trên toàn bộ trục số (bán kính hội tụ của nó là).

Nếu chức năng f (x) có trên một số khoảng có chứa một điểm một, các dẫn xuất của tất cả các lệnh, thì công thức Taylor có thể được áp dụng cho nó:

ở đâu rn- cái gọi là số hạng dư hoặc phần còn lại của chuỗi, nó có thể được ước tính bằng công thức Lagrange:

, trong đó số x được đặt giữa X và một.

Nếu cho một số giá trị x r n®0 lúc N® ¥, sau đó trong giới hạn công thức Taylor cho giá trị này biến thành công thức hội tụ Chuỗi Taylor:

Vì vậy, hàm f (x) có thể được mở rộng thành một chuỗi Taylor tại điểm được xem xét X, nếu:

1) nó có các dẫn xuất của tất cả các lệnh;

2) chuỗi đã xây dựng hội tụ tại điểm này.

Tại một= 0 chúng tôi nhận được một chuỗi có tên là gần Maclaurin:

ví dụ 1 f (x) = 2x.

Quyết định. Hãy để chúng tôi tìm các giá trị của hàm và các đạo hàm của nó tại X=0

f (x) = 2x, f ( 0) = 2 0 =1;

f ¢ (x) = 2x ln2, f ¢ ( 0) = 2 0 ln2 = ln2;

f ¢¢ (x) = 2x Năm 2 2, f ¢¢ ( 0) = 2 0 log 2 2 = log 2 2;

f (n) (x) = 2x ln N 2, f (n) ( 0) = 2 0 ln N 2 = ln N 2.

Thay các giá trị thu được của các đạo hàm vào công thức chuỗi Taylor, ta được:

Bán kính hội tụ của chuỗi này bằng vô cực, vì vậy khai triển này có giá trị đối với - ¥