Một Lò Xo Nhẹ Có Chiều Dài Tự Nhiên L0, độ Cứng K0 = 16 N/m, được Cắt

Lời giải của Tự Học 365

Giải chi tiết:

Đáp án B

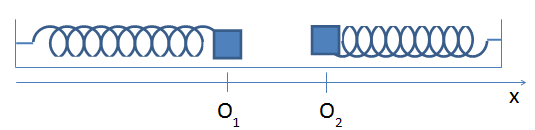
Ta có:   

$$\eqalign{ & {k_1}{l_1} = {k_2}{l_2} = {k_0}{l_0} \cr & \to {k_1} = {{{k_0}{l_0}} \over {{l_1}}} = {{{k_0}{l_0}} \over {0,8{l_0}}} = 20N/m;{k_2} = {{{k_0}{l_0}} \over {{l_2}}} = {{{k_0}{l_0}} \over {0,2{l_0}}} = 80N/m \cr & {O_1}{O_2} = 12cm;{W_{t\max }} = 0,1J = {{k{A^2}} \over 2} \cr & \to {A_1} = \sqrt {{{0,2} \over {{k_1}}}} = 0,1m = 10cm;{\rm{ }}{A_2} = \sqrt {{{0,2} \over {{k_2}}}} = 0,05m = 5cm \cr} $$

Tần số góc dao động của mỗi vật:  $${\omega _1} = \sqrt {{{{k_1}} \over m}}  = 2\pi ;{\rm{ }}{\omega _2} = \sqrt {{{{k_2}} \over m}}  = 4\pi $$

Phương trình dao động mỗi vật ứng với các vị trí cân bằng của chúng:

$$\eqalign{ & {x_1} = {A_1}\cos \left( {{\omega _1} + {\varphi _1}} \right) = 10\cos \left( {2\pi t - \pi } \right) \cr & {x_2} = {A_2}\cos \left( {{\omega _2} + {\varphi _2}} \right) = 5\cos \left( {4\pi t} \right) \cr} $$

Ta có khoảng cách hai vật tại một điểm bất kì: 

$$\eqalign{ & d = \left| {{O_1}{O_2} + {x_1} + {x_2}} \right| = \left| {12 + 10\cos \left( {2\pi t - \pi } \right) + 5\cos \left( {4\pi t} \right)} \right| \cr & = \left| {12 + 10\cos \left( {2\pi t} \right) + 5(2{{\cos }^2}\left( {2\pi t} \right) - 1)} \right| = \left| {7 + 10({{\cos }^2}\left( {2\pi t} \right) + \cos \left( {2\pi t} \right))} \right| \cr & = \left| {7 + 10({{\cos }^2}\left( {2\pi t} \right) + 2{1 \over 2}\cos \left( {2\pi t} \right) + {1 \over 4}) - {{10} \over 4}} \right| = \left| {4,5 + 10{{(\cos \left( {2\pi t} \right) + {1 \over 2})}^2}} \right| \cr} $$

Vậy khoảng cách nhỏ nhất giữa hai vật dmin =4,5 cm

xảy ra khi:   

$$\cos \left( {2\pi t} \right) = - {1 \over 2} \to 2\pi t = \pm {{2\pi } \over 3} + k2\pi \to \left[ \matrix{ t = {1 \over 3} + k({\rm{k = 0}},{\rm{1}},{\rm{2}},..) \hfill \cr t = - {1 \over 3} + k({\rm{k = 1}},{\rm{2}},..) \hfill \cr} \right.$$

Từ đó suy ra tmin=1/3