Một Số Bài Tập Liên Quan Tới Căn Thức Bậc Hai - Học Toán 123

Trang chủ » Bài Tập Căn Bậc Hai Lớp 9 Nâng Cao » Một Số Bài Tập Liên Quan Tới Căn Thức Bậc Hai - Học Toán 123

Có thể bạn quan tâm

MỤC LỤC

LÝ THUYẾT CĂN THỨC BẬC HAI

Kiến thức cần nhớ:

Một số bài tập liên quan tới căn thức bậc hai

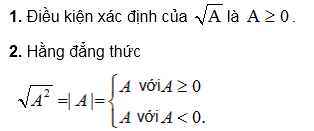
Các ví dụ:

Ví dụ 1: Tìm các giá trị của x để các biểu thức sau có nghĩa:

Một số bài tập liên quan tới căn thức bậc hai

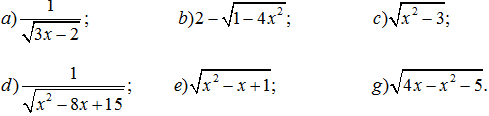
Giải

Một số bài tập liên quan tới căn thức bậc hai

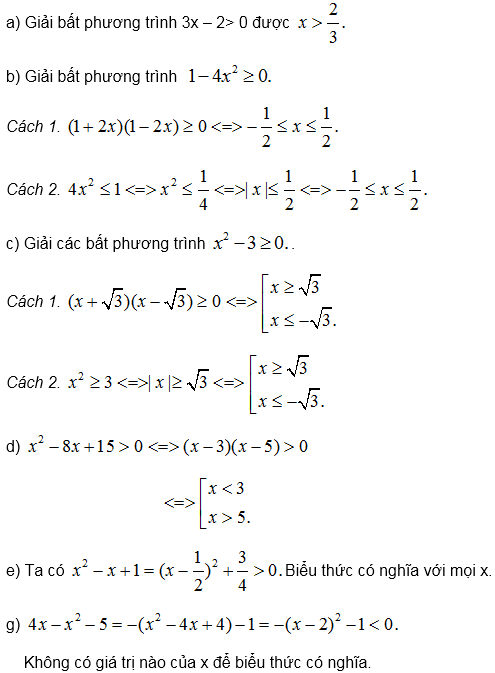
*Chú ý:

Muốn tìm các giá trị của x để biểu thức $\sqrt{A}$ có nghĩa, ta phải giải bất phương trình A ≥ 0.

Nếu A là nhị thức bậc nhất (câu a), ta phải giải bất phương trình bậc nhất một ẩn.

Nếu A là đa thức bậc hai (các câu còn lại), ta phải giải bất phương trình bậc hai (xem ví dụ 40). Ta chú ý các dạng sau :

a)  Nếu A phân tích được thành nhân tử (các câu b, c, d) ta giải bất phương trình tích bằng xét dấu các nhị thức bậc nhất.

Trường hợp bất phương trình có dạng $x^{2} \leq \mathrm{a}$ (câu b) hoặc $x^{2} \geq a$ (câu c) trong đó a là hằng số dương, ta có thể giải thích bằng cách:

$x^{2} \leq a<=>|x| \leq \sqrt{a}<=>-\sqrt{a} \leq x \leq \sqrt{a}$

$ x^{2}\ge a<=>|x|\ge \sqrt{a}\Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x\ge \sqrt{a}} \\ {x\le -\sqrt{a}} \end{array}} \right.$

b) Nếu A không phân tích được thành nhân tử (các câu e, g), ta sẽ chứng tỏ rằng biểu thức A :

–    Luôn luôn có giá trị dương (khi đó $\sqrt{A}$ có nghĩa với mọi x) ;

–    Hoặc luôn luôn có giá trị âm (khi đó $\sqrt{A}$ không có nghĩa với mọi x).

Ví dụ 2: Cho biểu thức $A=3 x-1-\sqrt{4 x^{2}+9-12 x}$

a) Rút gọn biểu thức A.

b) Tìm giá trị của x để A = 3.

Một số bài tập liên quan tới căn thức bậc hai

BÀI TẬP

1. Tìm giá trị của x để các biểu thức sau có nghĩa:

Một số bài tập liên quan tới căn thức bậc hai

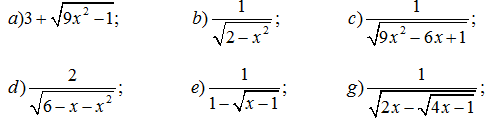
2. Rút gọn các biểu thức:

Một số bài tập liên quan tới căn thức bậc hai

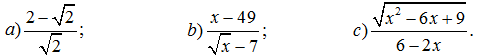
3. Rút gọn các biểu thức:

Một số bài tập liên quan tới căn thức bậc hai

4. Với các giá trị nào của a và b thì: $\sqrt{a^{2}\left(b^{2}-2 b+1\right)}=a(1-b)$

5. Rút gọn biểu thức $A=2 x-1-\sqrt{x^{2}-x+\dfrac{1}{4}}$ rồi tìm giá trị của $x$ để $A=\dfrac{3}{2}$

6. Giải các phương trình:

Một số bài tập liên quan tới căn thức bậc hai

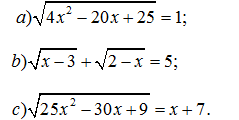
7. Tìm giá trị nhỏ nhất của biểu thức: $A=\sqrt{4 x^{2}-4 x+1}+\sqrt{4 x^{2}-12 x+9}$.

Từ khóa » Bài Tập Căn Bậc Hai Lớp 9 Nâng Cao