Một Số Bài Tập Toán Nâng Cao Lớp 9

Trang chủ » Các Dạng Toán Lớp 9 Nâng Cao » Một Số Bài Tập Toán Nâng Cao Lớp 9

Có thể bạn quan tâm

Một số bài tập Toán nâng cao lớp 9 Chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán Bài trước Tải về Bài sau Lớp: Lớp 9 Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Bài tập Toán nâng cao lớp 9

  • A. CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI VÀ NĂNG KHIẾU
  • B. ĐÁP ÁN CHI TIẾT CỦA BÀI TẬP

Nhằm mang đến cho các em học sinh ôn luyện đội tuyển học sinh giỏi, cũng như thầy cô giáo có tài liệu luyện thi cho học sinh, VnDoc gửi tới các bạn tài liệu Một số bài tập Toán nâng cao lớp 9. Đây là tài liệu hữu ích dành cho bồi dưỡng học sinh giỏi môn Toán lớp 9, ôn thi vào lớp 10 môn Toán. Mời thầy cô và các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.

A. CHUYÊN ĐỀ BỒI DƯỠNG HỌC SINH GIỎI VÀ NĂNG KHIẾU

Câu 1. Chứng minh √7 là số vô tỉ.

Câu 2.

a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)

b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)

Câu 3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.

Câu 4.

a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:

b) Cho a, b, c > 0. Chứng minh rằng:

c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.

Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.

Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.

Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)

Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|

Câu 9.

a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a

b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8

Câu 10. Chứng minh các bất đẳng thức:

a) (a + b)2 ≤ 2(a2 + b2)

b) (a + b + c)2 ≤ 3(a2 + b2 + c2)

Câu 11. Tìm các giá trị của x sao cho:

a) |2x – 3| = |1 – x|

b) x2 – 4x ≤ 5

c) 2x(2x – 1) ≤ 2x – 1.

Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)

Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.

Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.

Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:

x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0

Câu 16. Tìm giá trị lớn nhất của biểu thức:

Câu 17. So sánh các số thực sau (không dùng máy tính):

Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3

Câu 19. Giải phương trình: .

Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.

Câu 21. Cho .

Hãy so sánh S và .

Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.

Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng: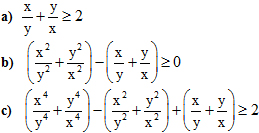

Câu 24. Chứng minh rằng các số sau là số vô tỉ:

Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?

Câu 26. Cho các số x và y khác 0. Chứng minh rằng:

Câu 27. Cho các số x, y, z dương. Chứng minh rằng:

Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.

Câu 29. Chứng minh các bất đẳng thức:

a) (a + b)2 ≤ 2(a2 + b2)

b) (a + b + c)2 ≤ 3(a2 + b2 + c2)

c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).

Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.

Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].

Câu 32. Tìm giá trị lớn nhất của biểu thức:

Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z > 0.

Câu 34. Tìm giá trị nhỏ nhất của: A = x2 + y2 biết x + y = 4.

Câu 35. Tìm giá trị lớn nhất của: A = xyz(x + y)(y + z)(z + x) với x, y, z ≥ 0; x + y + z = 1.

Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:

a) ab và a/b là số vô tỉ.

b) a + b và a/b là số hữu tỉ (a + b ≠ 0)

c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)

Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)

Câu 38. Cho a, b, c, d > 0. Chứng minh:

Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1

Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.

Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa: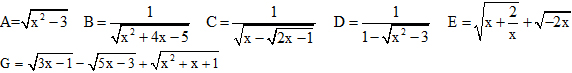

Câu 42. a) Chứng minh rằng: | A + B | ≤ | A | + | B |. Dấu “ = ” xảy ra khi nào?

b) Tìm giá trị nhỏ nhất của biểu thức sau: .

c) Giải phương trình:

Câu 43. Giải phương trình: .

Câu 44. Tìm các giá trị của x để các biểu thức sau có nghĩa:

Câu 45. Giải phương trình: \frac{x^{2} - 3x}{\sqrt{x - 3}} = 0

Câu 46. Tìm giá trị nhỏ nhất của biểu thức : A = \sqrt{x} + x.

Câu 47. Tìm giá trị lớn nhất của biểu thức: B = \sqrt{3 - x} + x

Câu 48. So sánh:

a) a = \sqrt{2 + \sqrt{3}}\ \ \ và\ \ \ b = \frac{\sqrt{3} + 1}{\sqrt{2}}

b) \sqrt{5 - \sqrt{13 + 4\sqrt{3}}}\ \ \ và\ \ \ \sqrt{3} - 1

c) \sqrt{n + 2} - \sqrt{n + 1}\ \ \ và\ \ \ \sqrt{n + 1} - \sqrt{n} (n là số nguyên dương)

Câu 49. Với giá trị nào của x, biểu thức sau đạt giá trị nhỏ nhấ: A = 1 - \sqrt{1 - 6x + 9x^{2}} + (3x - 1)^{2}.

Câu 50. Tính:

a,\sqrt{4 - 2\sqrt{3}}

b,\sqrt{11 + 6\sqrt{2}}

c,\sqrt{27 - 10\sqrt{2}}

d,A = \sqrt{m^{2} + 8m + 16} + \sqrt{m^{2} - 8m + 16}

e)\ \ \ B = \sqrt{n + 2\sqrt{n - 1}} + \sqrt{n - 2\sqrt{n - 1}} (n ≥ 1)

Câu 51. Rút gọn biểu thức: M =\frac{8\sqrt{41}}{\sqrt{45 + 4\sqrt{41}} + \sqrt{45 -4\sqrt{41}}}.

Câu 52. Tìm các số x, y, z thỏa mãn đẳng thức: (2x - y)^{2} + (y - 2)^{2} + \sqrt{(x + y + z)^{2}} = 0

Câu 53. Tìm giá trị nhỏ nhất của biểu thức: P = \sqrt{25x^{2} - 20x + 4} + \sqrt{25x^{2} - 30x + 9}.

Câu 54. Giải các phương trình sau:

a,\sqrt{x^{2} - x - 2} - \sqrt{x - 2} = 0

b,\sqrt{x^{2} - 1} + 1 = x^{2}

c,\sqrt{x^{2} - x} + \sqrt{x^{2} + x - 2} = 0

Câu 55. Cho hai số thực x và y thỏa mãn các điều kiện: xy = 1 và x > y. CMR: \frac{x^{2} + y^{2}}{x - y} \geq 2\sqrt{2}.

Câu 56. Rút gọn các biểu thức:

a,\sqrt{13 + 30\sqrt{2 + \sqrt{9 + 4\sqrt{2}}}}

b,\sqrt{m + 2\sqrt{m - 1}} + \sqrt{m - 2\sqrt{m - 1}}

c,\sqrt{2 + \sqrt{3}}.\sqrt{2 + \sqrt{2 + \sqrt{3}}}.\sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{3}}}}.\sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{3}}}}

d,\sqrt{227 - 30\sqrt{2}} + \sqrt{123 + 22\sqrt{2}}

Câu 57. Chứng minh rằng \sqrt{2 + \sqrt{3}} = \frac{\sqrt{6}}{2} + \frac{\sqrt{2}}{2}.

Câu 58. Rút gọn các biểu thức:

a,C = \frac{\sqrt{6 + 2\left( \sqrt{6} + \sqrt{3} + \sqrt{2} \right)} - \sqrt{6 - 2\left( \sqrt{6} - \sqrt{3} + \sqrt{2} \right)}}{\sqrt{2}}

b,D = \frac{\sqrt{9 - 6\sqrt{2}} - \sqrt{6}}{\sqrt{3}}

Câu 59. So sánh:

a,\sqrt{\sqrt{6 + \sqrt{20}}};\sqrt{1 + \sqrt{6}}

b,\sqrt{\sqrt{17 + 12\sqrt{2}}};\sqrt{2} + 1

c,\sqrt{\sqrt{28 - 16\sqrt{3}}};\sqrt{3} - 2

Câu 60. Cho biểu thức: A = \sqrt{x - \sqrt{x^{2} - 4x + 4}}

a. Tìm tập xác định của biểu thức A.

b. Rút gọn biểu thức A.

B. ĐÁP ÁN CHI TIẾT CỦA BÀI TẬP

1. Giả sử \sqrt{7} là số hữu tỉ \Rightarrow \sqrt{7} = \frac{m}{n} (tối giản). Suy ra 7 = \frac{m^{2}}{n^{2}} hay 7n^{2} = m^{2}(1). Đẳng thức này chứng tỏ m^{2}:7 mà 7 là số nguyên tố nên m:7.

Đặt m = 7k\ (k \in Z), ta m^{2} = 49k^{2}(2).

Từ (1) và (2) suy ra 7n^{2} = 49k^{2} nên n^{2} = 7k^{2} (3).

Từ (3) ta lại có n^{2} \vdots 7 và vì 7 là số nguyên tố nên n : 7. m và n cùng chia hết cho 7 nên phân số \frac{m}{n} không tối giản, trái giả thiết.

Vậy \sqrt{7} không phải là số hữu tỉ; do đó \sqrt{7} là số vô tỉ.

2. Khai triển vế trái và đặt nhân tử chung, ta được vế phải. Từ a) \Rightarrow b) vì (ad - bc)^{2} \geq 0.

3. Cách 1: Từ x + y = 2 ta có y = 2 - x. Do đó: S = x^{2} + (2 - x)^{2} = 2(x - 1)^{2} + 2 \geq 2.

Vậy minS = 2 \Leftrightarrow x = y = 1.

Cách 2: Áp dụng bất đẳng thức Bunhiacopxki với a = x,c = 1,\text{\ }b = y,d = 1, ta có : (x + y)^{2} \leq \left( x^{2} + y^{2} \right)(1 + 1) \Leftrightarrow 4 \leq 2\left( x^{2} + y^{2} \right) = 2S \Leftrightarrow S \geq 2. \Rightarrow mimS = 2 khi x = y = 1

4. b) Áp dụng bất đẳng thức Cauchy cho các cặp số dương \frac{bc}{a} và \frac{ca}{b};\frac{bc}{a} và \frac{ab}{c};\frac{ca}{b} và \frac{ab}{c}, ta lần lượt có:

\frac{bc}{a} + \frac{ca}{\text{\ }b} \geq 2\sqrt{\frac{bc}{a} \cdot \frac{ca}{\text{\ }b}} = 2c;\frac{bc}{a} + \frac{ab}{c} \geq 2\sqrt{\frac{bc}{a} \cdot \frac{ab}{c}} = 2\text{\ }b;\frac{ca}{\text{\ }b} + \frac{ab}{c} \geq 2\sqrt{\frac{ca}{\text{\ }b} \cdot \frac{ab}{c}} = 2a\text{~~}

Cộng từng vế ta được bất đẳng thức cần chứng minh. Dấu bằng xảy ra khi a = b = c.c) Với các số dương 3a và 5b, theo bất đẳng thức Cauchy ta có : \frac{3a + 5b}{2} \geq \sqrt{3a \cdot 5b}.\Leftrightarrow (3a + 5b)^{2} \geq 4.15P( vì P = a.b) \Leftrightarrow 12^{2} \geq 60P \Leftrightarrow P \leq \frac{12}{5} \Rightarrow maxP = \frac{12}{5}.

Dấu bằng xảy ra khi 3a = 5\text{\ }b = 12:2 \Leftrightarrow a = 2;b = 6/5.5. Ta có b = 1 - a, do đó M = a^{3} + (1 - a)^{3} = 3(a - 1/2)^{2} + 1/4 \geq 1/4. Dấu "=" xảy ra khi a = 1/2.

Vậy \min M = 1/4 \Leftrightarrow a = b = 1/2.

6. Đặt a = 1 + x

\Rightarrow b^{3} = 2 - a^{3} = 2 - (1 + x)^{3}

= 1 - 3x - 3x^{2} - x^{3} \leq 1 - 3x + 3x^{2} - x^{3} = (1 - x)^{3}.

Suy ra: b \leq 1 - x.

Ta lại có a = 1 + x, nên : a + b \leq 1 + x + 1 - x = 2.Với a = 1,b = 1 thì a^{3} + b^{3} = 2 và a + b = 2. Vậy maxN = 2 khi a = b = 1.

7. Hiệu của vế trái và vế phải bằng (a - b)^{2}(a + b).

8. Vì |a + b| \geq 0,|a - b| \geq 0, nên: |a + b| > |a - b| \Leftrightarrow a^{2} + 2ab + b^{2} \geq a^{2} - 2ab + b^{2}

\Leftrightarrow 4ab > 0 \Leftrightarrow ab > 0. Vậy a và b là hai số cùng dấu.

9. a) Xét hiệu : (a + 1)^{2} - 4a = a^{2} + 2a + 1 - 4a = a^{2} - 2a + 1 = (a - 1)^{2} \geq 0.b) Ta có : (a + 1)^{2} \geq 4a;(b + 1)^{2}\geq 4b;(c + 1)^{2} \geq 4c và các bất đẳng thức này có hai vế đều dương, nên : \lbrack(a + 1)(b + 1)(c + 1)\rbrack^{2} \geq 64abc = 64.1 = 8^{2}.

Vậy (a + 1)(b + 1)(c + 1) \geq 8.

10. a) Ta có : (a + b)^{2} + (a - b)^{2} = 2\left( a^{2} + b^{2} \right). Do (a - b)^{2} \geq 0, nên (a + b)^{2} \leq 2\left( a^{2} + b^{2} \right).

b) Xét : (a + b + c)^{2} + (a - b)^{2} + (a - c)^{2} + (b - c)^{2}.

Khai triển và rút gọn, ta được : 3\left( a^{2} + b^{2} + c^{2} \right). Vậy : (a + b + c)^{2} \leq 3\left( a^{2} + b^{2} + c^{2} \right).11. a) |2x - 3| = |1 - x| \Leftrightarrow \left\lbrack \begin{matrix} \begin{matrix} 2x - 3 = 1 - x \\ 2x - 3 = x - 1 \\ \end{matrix} \\ \Leftrightarrow \left\lbrack \begin{matrix} 3x = 4 \\ x = 2 \\ \end{matrix} \Leftrightarrow \left\lbrack \begin{matrix} x = \frac{4}{3} \\ x = 2 \\ \end{matrix} \right.\ \right.\ \\ \end{matrix} \right.

b) x^{2} - 4x \leq 5 \Leftrightarrow (x - 2)^{2} \leq 3^{3} \Leftrightarrow |x - 2| \leq 3 \Leftrightarrow - 3 \leq x - 2 \leq 3 \Leftrightarrow - 1 \leq x \leq 5.

c) 2x(2x - 1) \leq 2x - 1 \Leftrightarrow (2x - 1)^{2} \leq 0.

Nhưng (2x - 1)^{2} \geq 0, nên chỉ có thể : 2x - 1 = 0

Vậy: x = 1/2.

11. a) |2x - 3| = |1 - x|\ \ \Leftrightarrow \ \ \left\lbrack \begin{matrix} 2x - 3 = 1 - x \\ 2x - 3 = x - 1 \end{matrix} \right.\ \

\Leftrightarrow \ \ \ \left\lbrack \begin{matrix} 3x = 4 \\ x = 2 \end{matrix} \right.\ \ \ \Leftrightarrow \ \ \ \left\lbrack \begin{matrix} x = \frac{4}{3} \\ x = 2 \end{matrix} \right.

b) x2 – 4x ≤ 5 ⇔ (x – 2)2 ≤ 33

⇔ | x – 2 | ≤ 3 ⇔ -3 ≤ x – 2 ≤ 3 ⇔ -1 ≤ x ≤ 5.

c) 2x(2x – 1) ≤ 2x – 1 ⇔ (2x – 1)2 ≤ 0.

Nhưng (2x – 1)2 ≥ 0, nên chỉ có thể: 2x – 1 = 0

Vậy : x = ½ .

12. Viết đẳng thức đã cho dưới dạng : a2 + b2 + c2 + d2 – ab – ac – ad = 0 (1). Nhân hai vế của (1) với 4 rồi đưa về dạng : a2 + (a – 2b)2 + (a – 2c)2 + (a – 2d)2 = 0 (2).

Do đó ta có:

a = a – 2b = a – 2c = a – 2d = 0 . Suy ra : a = b = c = d = 0.

13. 2M = (a + b – 2)2 + (a – 1)2 + (b – 1)2 + 2.1998 ≥ 2.1998 ⇒ M ≥ 1998.

Dấu “ = “ xảy ra khi có đồng thời : \left\{ \begin{matrix} a + b - 2 = 0 \\ a - 1 = 0 \\ b - 1 = 0 \end{matrix} \right. Vậy min M = 1998 ⇔ a = b = 1.

14. Giải tương tự bài 13.

15. Đưa đẳng thức đã cho về dạng: (x – 1)2 + 4(y – 1)2 + (x – 3)2 + 1 = 0.

16. A = \frac{1}{x^{2} - 4x + 9} = \frac{1}{(x - 2)^{2} + 5} \leq \frac{1}{5}.\ \ max\ A = \frac{1}{5}\ \ \Leftrightarrow \ \ x = 2.

17. a) \sqrt{7} + \sqrt{15} < \sqrt{9} + \sqrt{16} = 3 + 4 = 7. Vậy \sqrt{7} + \sqrt{15} < 7

b) \sqrt{17} + \sqrt{5} + 1 > \sqrt{16} + \sqrt{4} + 1

= 4 + 2 + 1 = 7 = \sqrt{49} > \sqrt{45}.

c) \frac{23 - 2\sqrt{19}}{3} < \frac{23 - 2\sqrt{16}}{3} = \frac{23 - 2.4}{3} = 5 = \sqrt{25} < \sqrt{27}.

d) Giả sử \sqrt{3\sqrt{2}} > \sqrt{2\sqrt{3}}\ \ \Leftrightarrow \ \ \left( \sqrt{3\sqrt{2}} \right)^{2} > \left( \sqrt{2\sqrt{3}} \right)^{2}\

\Leftrightarrow \ \ 3\sqrt{2} > 2\sqrt{3}\ \ \Leftrightarrow \ \ \sqrt{18} > \sqrt{12}\ \ \Leftrightarrow \ \ 18 > 12.

Bất đẳng thức cuối cùng đúng, nên : \sqrt{3\sqrt{2}} > \sqrt{2\sqrt{3}}.

18. Các số đó có thể là 1,42 và \frac{\sqrt{2} + \sqrt{3}}{2}

19. Viết lại phương trình dưới dạng : \sqrt{3(x + 1)^{2} + 4} + \sqrt{5(x + 1)^{2} + 16} = 6 - (x + 1)^{2}.

Vế trái của phương trình không nhỏ hơn 6, còn vế phải không lớn hơn 6. Vậy đẳng thức chỉ xảy ra khi cả hai vế đều bằng 6, suy ra x = -1.

20. Bất đẳng thức Cauchy \sqrt{ab} \leq \frac{a + b}{2} viết lại dưới dạng ab \leq \left( \frac{a + b}{2} \right)^{2} (*) (a, b ≥ 0).

Áp dụng bất dẳng thức Cauchy dưới dạng (*) với hai số dương 2x và xy ta được :

2x.xy \leq \left( \frac{2x + xy}{2} \right)^{2} = 4

Dấu “ = “ xảy ra khi : 2x = xy = 4 : 2 tức là khi x = 1, y = 2. ⇒ max A = 2 ⇔ x = 2, y = 2.

21. Bất đẳng thức Cauchy viết lại dưới dạng : \frac{1}{\sqrt{ab}} > \frac{2}{a + b}. Áp dụng ta có S > 2.\frac{1998}{1999}.

22. Chứng minh như bài 1.

23. a) \frac{x}{y} + \frac{y}{x} - 2 = \frac{x^{2} + y^{2} - 2xy}{xy} = \frac{(x - y)^{2}}{xy} \geq 0. Vậy \frac{x}{y} + \frac{y}{x} \geq 2

b) Ta có:

A = \left( \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \right) - \left( \frac{x}{y} + \frac{y}{x} \right)

= \left( \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \right) - 2\left( \frac{x}{y} + \frac{y}{x} \right) + \left( \frac{x}{y} + \frac{y}{x} \right).

Theo câu a:

A \geq \left( \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \right) - 2\left( \frac{x}{y} + \frac{y}{x} \right) + 2 = \left( \frac{x}{y} - 1 \right)^{2} + \left( \frac{y}{x} - 1 \right)^{2} \geq 0

c) Từ câu b suy ra: \left( \frac{x^{4}}{y^{4}} + \frac{y^{4}}{x^{4}} \right) - \left( \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \right) \geq 0. Vì \frac{x}{y} + \frac{y}{x} \geq 2 (câu a).

Do đó:

\left( \frac{x^{4}}{y^{4}} + \frac{y^{4}}{x^{4}} \right) - \left( \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \right) + \left( \frac{x}{y} + \frac{y}{x} \right) \geq 2.

24. a) Giả sử \sqrt{1 + \sqrt{2}} = m (m: số hữu tỉ) ⇒ \sqrt{2} = m2 – 1 ⇒ \sqrt{2} là số hữu tỉ (vô lí)

b) Giả sử m + \frac{\sqrt{3}}{n} = a (a : số hữu tỉ) ⇒ \frac{\sqrt{3}}{n} = a – m

⇒ \sqrt{3} = n(a – m) ⇒ \sqrt{3} là số hữu tỉ, vô lí.

25. Có, chẳng hạn \sqrt{2} + (5 - \sqrt{2}) = 5

26. Đặt \frac{x}{y} + \frac{y}{x} = a\ \ \ \Rightarrow \ \ \ \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} + 2 = a^{2}. Dễ dàng chứng minh \ \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} \geq 2 nên a2 ≥ 4, do đó

| a | ≥ 2 (1). Bất đẳng thức phải chứng minh tương đương với : a2 – 2 + 4 ≥ 3a

⇔ a2 – 3a + 2 ≥ 0 ⇔ (a – 1)(a – 2) ≥0 (2)

Từ (1) suy ra a ≥ 2 hoặc a ≤ -2.

Nếu a ≥ 2 thì (2) đúng. Nếu a ≤ -2 thì (2) cũng đúng. Bài toán được chứng minh.

27. Bất đẳng thức phải chứng minh tương đương với :

\frac{x^{4}z^{2} + y^{4}x^{2} + z^{4}x^{2} - \left( x^{2}z + y^{2}x + z^{2}y \right)xyz}{x^{2}y^{2}z^{2}} \geq 0.

Cần chứng minh tử không âm, tức là : x3z2(x – y) + y3x2(y – z) + z3y2(z – x) ≥ 0. (1)

Biểu thức không đổi khi hoán vị vòng x 🡪 y 🡪 z 🡪 x nên có thể giả sử x là số lớn nhất. Xét hai trường hợp :

a) x ≥ y ≥ z > 0. Tách z – x ở (1) thành – (x – y + y – z), (1) tương đương với :

x3z2(x – y) + y3x2(y – z) – z3y2(x – y) – z3y2(y – z) ≥ 0

⇔ z2(x – y)(x3 – y2z) + y2(y – z)(yx2 – z3) ≥ 0

Dễ thấy x – y ≥ 0 , x3 – y2z ≥ 0 , y – z ≥ 0 , yx2 – z3 ≥ 0 nên bất đẳng thức trên đúng.

b) x ≥ z ≥ y > 0. Tách x – y ở (1) thành x – z + z – y , (1) tương đương với :

x3z2(x – z) + x3z2(z – y) – y3x2(z – y) – z3y2(x – z) ≥ 0

⇔ z2(x – z)(x3 – zy2) + x2(xz2 – y3)(z – y) ≥ 0

Dễ thấy bất đẳng thức trên dúng.

Cách khác : Biến đổi bất đẳng thức phải chứng minh tương đương với :

\left( \frac{x}{y} - 1 \right)^{2} + \left( \frac{y}{z} - 1 \right)^{2} + \left( \frac{z}{x} - 1 \right)^{2} + \left( \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \right)\ \ \geq 3.

28. Chứng minh bằng phản chứng. Giả sử tổng của số hữu tỉ a với số vô tỉ b là số hữu tỉ c. Ta có : b = c – a. Ta thấy, hiệu của hai số hữu tỉ c và a là số hữu tỉ, nên b là số hữu tỉ, trái với giả thiết. Vậy c phải là số vô tỉ.

29. a) Ta có : (a + b)2 + (a – b)2 = 2(a2 + b2) ⇒ (a + b)2 ≤ 2(a2 + b2).

b) Xét : (a + b + c)2 + (a – b)2 + (a – c)2 + (b – c)2. Khai triển và rút gọn ta được:

3(a2 + b2 + c2). Vậy : (a + b + c)2 ≤ 3(a2 + b2 + c2)

c) Tương tự như câu b

30. Giả sử a + b > 2 ⇒ (a + b)3 > 8 ⇔ a3 + b3 + 3ab(a + b) > 8 ⇔ 2 + 3ab(a + b) > 8

⇒ ab(a + b) > 2 ⇒ ab(a + b) > a3 + b3. Chia hai vế cho số dương a + b : ab > a2 – ab + b2

⇒ (a – b)2 < 0, vô lí. Vậy a + b ≤ 2.

31. Cách 1: Ta có : \lbrack x\rbrack ≤ x ; \lbrack y\rbrack ≤ y nên \lbrack x\rbrack + \lbrack y\rbrack ≤ x + y. Suy ra \lbrack x\rbrack + \lbrack y\rbrack là số nguyên không vượt quá x + y (1). Theo định nghĩa phần nguyên, \lbrack x + y\rbrack là số nguyên lớn nhất không vượt quá x + y (2). Từ (1) và (2) suy ra: \lbrack x\rbrack + \lbrack y\rbrack ≤ \lbrack x + y\rbrack.

Cách 2 : Theo định nghĩa phần nguyên: 0 ≤ x - \lbrack x\rbrack < 1 ; 0 ≤ y - \lbrack y\rbrack < 1.

Suy ra : 0 ≤ (x + y) – (\lbrack x\rbrack + \lbrack y\rbrack) < 2. Xét hai trường hợp :

  • Nếu 0 ≤ (x + y) – (\lbrack x\rbrack + \lbrack y\rbrack) < 1 thì \lbrack x + y\rbrack = \lbrack x\rbrack + \lbrack y\rbrack (1)

  • Nếu 1 ≤ (x + y) – (\lbrack x\rbrack + \lbrack y\rbrack) < 2 thì 0≤ x + y) – (\lbrack x\rbrack + \lbrack y\rbrack + 1) < 1 nên\lbrack x + y\rbrack = \lbrack x\rbrack + \lbrack y\rbrack + 1 (2). Trong cả hai trường hợp ta đều có: \lbrack x\rbrack + \lbrack y\rbrack ≤ \lbrack x + y\rbrack

32. Ta có x2 – 6x + 17 = (x – 3)2 + 8 ≥ 8 nên tử và mẫu của A là các số dương, suy ra A > 0 do đó: A lớn nhất ⇔ \frac{1}{A} nhỏ nhất ⇔ x2 – 6x + 17 nhỏ nhất.

Vậy max A = \frac{1}{8} ⇔ x = 3.

33. Không được dùng phép hoán vị vòng quanh x 🡪 y 🡪 z 🡪 x và giả sử x ≥ y ≥ z.

Cách 1 : Áp dụng bất đẳng thức Cauchy cho 3 số dương x, y, z :

A = \frac{x}{y} + \frac{y}{z} + \frac{z}{x}\ \ \ \geq \ \ \ 3\sqrt[3]{\frac{x}{y}.\frac{y}{z}.\frac{z}{x}}\ \ \ = \ \ \ 3

Do đó \min\left( \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \right) = 3\ \ \ \Leftrightarrow \ \ \ \frac{x}{y} = \frac{y}{z} = \frac{z}{x}\ \ \ \Leftrightarrow x = y = z

Cách 2 : Ta có : \frac{x}{y} + \frac{y}{z} + \frac{z}{x} = \left( \frac{x}{y} + \frac{y}{x} \right) + \left( \frac{y}{z} + \frac{z}{x} - \frac{y}{x} \right).

Ta đã có \frac{x}{y} + \frac{y}{x} \geq 2 (do x, y > 0) nên để chứng minh \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \geq 3 ta chỉ cần chứng minh : \frac{y}{z} + \frac{z}{x} - \frac{y}{x} \geq 1 (1)

(1) ⇔ xy + z2 – yz ≥ xz (nhân hai vế với số dương xz)

⇔ xy + z2 – yz – xz ≥ 0 ⇔ y(x – z) – z(x – z) ≥ 0 ⇔ (x – z)(y – z) ≥ 0 (2)

(2) đúng với giả thiết rằng z là số nhỏ nhất trong 3 số x, y, z, do đó (1) đúng. Từ đó tìm được giá trị nhỏ nhất của \frac{x}{y} + \frac{y}{z} + \frac{z}{x}.

34. Ta có x + y = 4 ⇒ x2 + 2xy + y2 = 16.

Ta lại có (x – y)2 ≥ 0 ⇒ x2 – 2xy + y2 ≥ 0. Từ đó suy ra 2(x2 + y2) ≥ 16 ⇒ x2 + y2 ≥ 8. min A = 8 khi và chỉ khi x = y = 2.

35. Áp dụng bất đẳng thức Cauchy cho ba số không âm:

1 = x + y + z ≥ 3.\sqrt[3]{xyz} (1)

2 = (x + y) + (y + z) + (z + x) ≥ 3.\sqrt[3]{(x + y)(y + z)(z + x)} (2)

Nhân từng vế của (1) với (2) (do hai vế đều không âm) : 2 ≥ 9.\sqrt[3]{A} ⇒ A ≤ \left( \frac{2}{9} \right)^{3}

max A = \left( \frac{2}{9} \right)^{3} khi và chỉ khi x = y = z = \frac{1}{3}.

36. a) Có thể. b, c) Không thể.

37. Hiệu của vế trái và vế phải bằng (a – b)2(a + b).

38. Áp dụng bất đẳng thức \frac{1}{xy} \geq \frac{4}{(x + y)^{2}} với x, y > 0:

\frac{a}{b + c} + \frac{c}{d + a} = \frac{a^{2} + ad + bc + c^{2}}{(b + c)(a + d)} \geq \frac{4(a^{2} + ad + bc + c^{2})}{(a + b + c + d)^{2}} (1)

Tương tự \frac{b}{c + d} + \frac{d}{a + b} \geq \frac{4(b^{2} + ab + cd + d^{2})}{(a + b + c + d)^{2}} (2)

Cộng (1) với (2)

\frac{a}{b + c} + \frac{b}{c + d} + \frac{c}{d + a} + \frac{d}{a + b} \geq \frac{4(a^{2} + b^{2} + c^{2} + d^{2} + ad + bc + ab + cd)}{(a + b + c + d)^{2}}= 4B

Cần chứng minh B ≥ \frac{1}{2}, bất đẳng thức này tương đương với:

2B ≥ 1 ⇔ 2(a2 + b2 + c2 + d2 + ad + bc + ab + cd) ≥ (a + b + c + d)2

⇔ a2 + b2 + c2 + d2 – 2ac – 2bd ≥ 0 ⇔ (a – c)2 + (b – d)2 ≥ 0: đúng.

39. - Nếu 0 ≤ x - \lbrack x\rbrack < ½ thì 0 ≤ 2x - 2\lbrack x\rbrack < 1 nên \lbrack 2x\rbrack = 2\lbrack x\rbrack.

- Nếu ½ ≤ x - \lbrack x\rbrack < 1 thì 1 ≤ 2x - 2\lbrack x\rbrack < 2 ⇒ 0 ≤ 2x – (2\lbrack x\rbrack + 1) < 1 ⇒ \lbrack 2x\rbrack = 2\lbrack x\rbrack + 1

40. Ta sẽ chứng minh tồn tại các số tự nhiên m, p sao cho:

96\underset{m\ chöõ\ \ soá\ 0}{\overset{000...00}{︸}} ≤ a + 15p < 97\underset{m\ chöõ\ \ soá\ 0}{\overset{000...00}{︸}}

Tức là 96 ≤ \frac{a}{10^{m}} + \frac{15p}{10^{m}} < 97 (1).

Gọi a + 15 là số có k chữ số : 10k – 1 ≤ a + 15 < 10k

⇒ \frac{1}{10} \leq \frac{a}{10^{k}} + \frac{15}{10^{k}} < 1 (2). Đặt x_{n} = \frac{a}{10^{k}} + \frac{15p}{10^{k}}. Theo (2) ta có x1 < 1 và \frac{15}{10^{k}} < 1.

Cho n nhận lần lượt các giá trị 2, 3, 4, …, các giá trị của xn tăng dần, mỗi lần tăng không quá 1 đơn vị, khi đó \left\lbrack x_{n} \right\rbrack sẽ trải qua các giá trị 1, 2, 3, … Đến một lúc nào đó ta có \left\lbrack x_{p} \right\rbrack = 96. Khi đó 96 ≤ xp < 97 tức là 96 ≤ \frac{a}{10^{k}} + \frac{15p}{10^{k}} < 97. Bất đẳng thức (1) được chứng minh.

42. a) Do hai vế của bất đẳng thức không âm nên ta có:

| A + B | ≤ | A | + | B | ⇔ | A + B |2 ≤ ( | A | + | B | )2

⇔ A2 + B2 + 2AB ≤ A2 + B2 + 2| AB | ⇔ AB ≤ | AB | (bất đẳng thức đúng)

Dấu “ = “ xảy ra khi AB ≥ 0.

b) Ta có : M = | x + 2 | + | x – 3 | = | x + 2 | + | 3 – x | ≥ | x + 2 + 3 – x | = 5.

Dấu “ = “ xảy ra khi và chỉ khi (x + 2)(3 – x) ≥ 0 ⇔ -2 ≤ x ≤ 3 (lập bảng xét dấu)

Vậy min M = 5 ⇔ -2 ≤ x ≤ 3.

c) Phương trình đã cho ⇔ | 2x + 5 | + | x – 4 | = | x + 9 | = | 2x + 5 + 4 – x |

⇔ (2x + 5)(4 – x) ≥ 0 ⇔ -5/2 ≤ x ≤ 4

43. Điều kiện tồn tại của phương trình: x2 – 4x – 5 ≥ 0 ⇔ \left\lbrack \begin{matrix} x \leq - 1 \\ x \geq 5 \end{matrix} \right.

Đặt ẩn phụ \sqrt{x^{2} - 4x - 5} = y \geq 0, ta được: 2y2 – 3y – 2 = 0 ⇔ (y – 2)(2y + 1) = 0.

45. Vô nghiệm

Mời bạn đọc tải tài liệu tham khảo đầy đủ của chúng tôi!

--------------------------------------------------------------

Ngoài tài liệu Một số bài tập Toán nâng cao lớp 9 mà VnDoc chia sẻ trên đây, các bạn có thể tham khảo thêm các tài liệu môn Toán lớp 9 khác được cập nhật liên tục trên VnDoc.

Từ khóa » Các Dạng Toán Lớp 9 Nâng Cao