Một Số Bài Toán Phương Trình Logarit Khác Cơ Số

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Đề thi
  • Học tiếng Anh
  • Giáo án
  • Bài giảng điện tử
  • Tài liệu Giáo viên
  • Tập huấn Giáo viên

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Download.vn Học tập Lớp 12 Toán 12 Một số bài toán phương trình logarit khác cơ số Tài liệu ôn tập môn Toán lớp 12 Tải về Bình luận

• 2

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo

Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua Zalo

Nhằm đem đến cho các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập môn Toán Download.vn xin giới thiệu tài liệu Một số bài toán phương trình logarit khác cơ số.

Để giải các dạng bài tập về phương trình logarit với cơ số khác nhau, nhiều học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về các phương trình cơ bản.Tài liệu này sẽ giới thiệu các phương pháp thường được áp dụng để giải dạng toán này. Bao gồm: Đổi cơ số; Đặt ẩn phụ để đưa về phương trình mũ; Biến đổi tương đương; Đánh giá hai vế. Hy vọng qua tài liệu này các bạn nắm vững được kiến thức giải nhanh các bài toán để đạt kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia. Mời các bạn cùng theo dõi.

Một số bài toán phương trình logarit khác cơ số

Chuaån bò cho kyø thi Ñaïi hoïc Page 1 VVVVài bài toán về phương trình logarit khác cơ số Huỳnh Đức Khánh – 0975.120.189 Descartes Giải tích – ĐH Quy Nhơn Phương trình logarit với cơ số khác nhau luôn là vấn đề gây khó dễ cho học sinh khi gặp phải trong các đề thi. Học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về các phương trình cơ bản. Tôi viết bài xin đóng góp vài bài mẫu về vấn đề này, nó được dùng các phương pháp: Đổi cơ số, đặt ẩn phụ để đưa về phương trình mũ, biến đổi tương đương, đánh giá hai vế. Ví dụ 1. Giải phương trình: 23420logxlogxlogxlogx++=. Điều kiện: x0>. Với điều kiện trên phương trình tương đương 23242202logxlog2.logxlog2.logxlog2.logx++= ()23420logx1log2log2log20⇔++−= 2logx0⇔= (do 34201log2log2log20++−≠) x1⇔= (thỏa mãn). Vậy phương trình có nghiệm x1=. Ví dụ 2. Giải phương trình: ()232logx3x13logx−−=. Điều kiện: 2x3x130361xx02−−>+⇔>>. Đặt: t2logxtx2=⇔=. Phương trình trở thành: ()tt3log43.213t−−= ttt43.2133⇔−−= ttt3121133444⇔=++. (*) Hàm số ttt312y133444=++ là tổng của các hàm nghịch biến nên y nghịch biến, hàm y1= là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất. Ta có: 3333121133444=++. Suy ra phương trình (*) có nghiệm t3=. Với 3t3x28=⇒== (thỏa mãn). Vậy phương trình có nghiệm duy nhất x8=. Chuaån bò cho kyø thi Ñaïi hoïc Page 2 Ví dụ 3. Giải phương trình: ()23log1xlogx+=. Điều kiện: x0>. Đặt: t3logxtx3=⇔=. Phương trình trở thành: ()t2log13t+= tt132⇔ += tt13122⇔+=. (*) Hàm số tt13y22=+ là tổng của các hàm nghịch biến nên y nghịch biến, hàm y1= là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất. Ta có: 2213122+=. Suy ra phương trình (*) có nghiệm t2=. Với 2t2x39=⇒== (thỏa mãn). Vậy phương trình có nghiệm duy nhất x9=. Ví dụ 4. Giải phương trình: ()()2232logx2x1logx2x++=+. (1) Điều kiện: 22x2x10x2x0x2x0++><−⇔>+>. Đặt: 2ux2x=+. Phương trình (1) trở thành: ()32logu1logu+=. (2)Xét phương trình (2). Ta đặt: t2logutu2=⇔=. Phương trình (2) trở thành: ()t3log21t+= tt213⇔+ = tt21133⇔+=. (3) Hàm số tt21y33=+ là tổng của các hàm nghịch biến nên y nghịch biến, hàm y1= là hàm hằng. Do đó phương trình (3) có nghiệm duy nhất. Ta có: 1121133+=. Suy ra phương trình (3) có nghiệm t1=. Với 12x13t1u22x2x2x13=−−=⇒==⇒+=⇔=−+ (thỏa mãn). Vậy phương trình có nghiệm x13; x13=−−=−+. 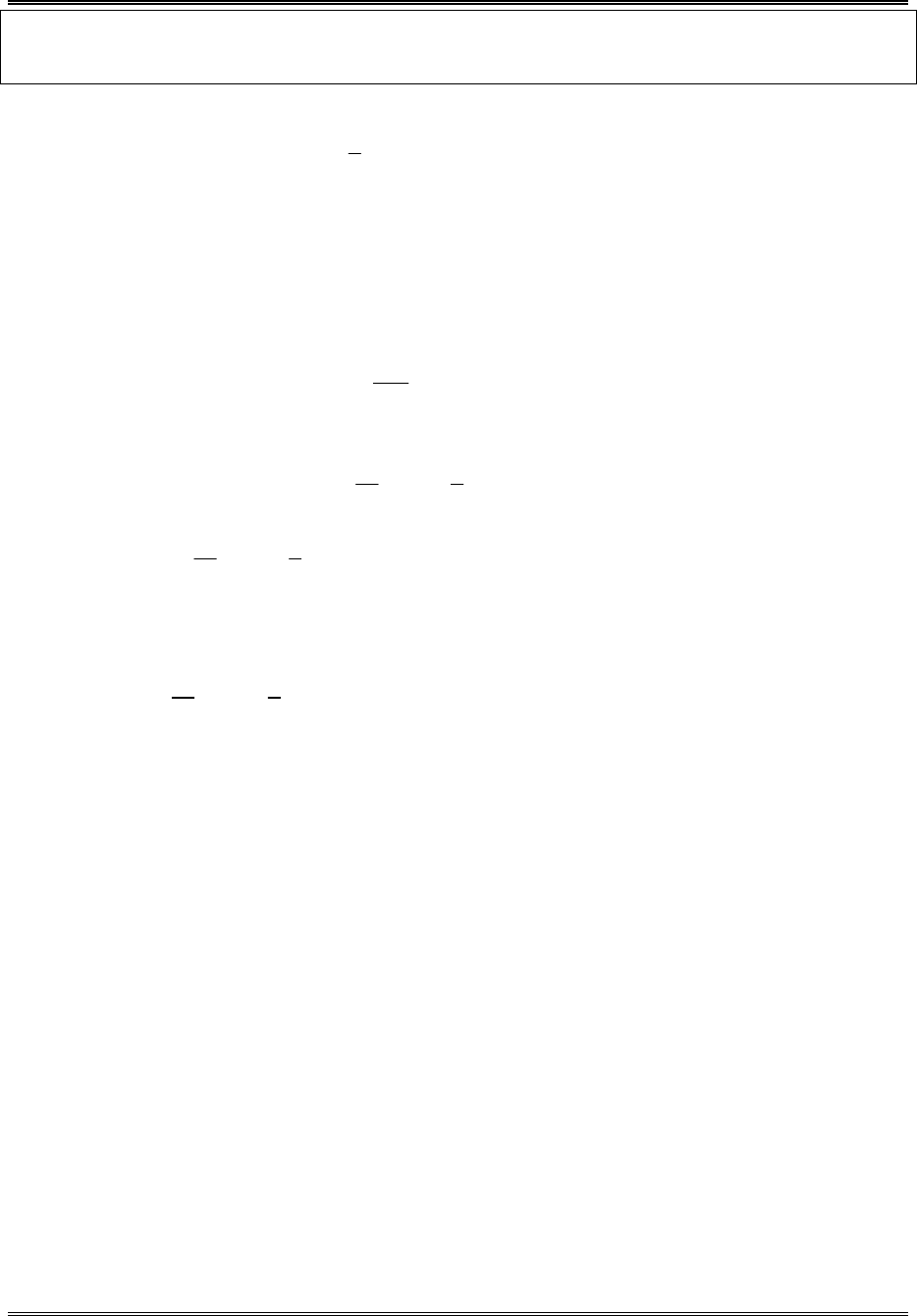Chuaån bò cho kyø thi Ñaïi hoïc Page 3 Ví dụ 5. Giải phương trình: ()()35logx1log3x14+++=. Điều kiện: x101x3x103+>⇔>−+>. Đặt: ()t3logx1tx13+=⇔+=, suy ra: t3x13.32+=−. Phương trình trở thành: ()t5tlog3.324+−= ()t5log3.324t⇔−=− t4t3.325−⇔−= tt6253.325⇔−= tt3.152.5625⇔−= tt1136252153⇔=+. Hàm số tt11y6252153=+ là tổng của các hàm nghịch biến nên y nghịch biến, hàm y3= là hàm hằng. Do đó phương trình có nghiệm duy nhất. Ta có: 221136252153=+. Suy ra phương trình có nghiệm t2=. Với 2t2x13x8=⇒+=⇔= (thỏa mãn). Vậy phương trình có nghiệm duy nhất x8=. Cách khác: ● Kiểm tra x8= là nghiệm của phương trình. ● Nếu x8> thì ()()()()()()333555logx1log812logx1log3x14log3x1log3.812+>+=⇒+++>+>+=. ● Nếu x8< thì ()()()()()()333555logx1log812logx1log3x14log3x1log3.812+<+=⇒+++<+<+=. Vậy phương trình có nghiệm duy nhất x8=. Chia sẻ bởi: Trịnh Thị Thanh

Tải về

Liên kết tải về Một số bài toán phương trình logarit khác cơ số 186,2 KB Tải về Tìm thêm: Toán 12

Có thể bạn quan tâm

• 

  Bài tập toán nâng cao lớp 8 - Toán nâng cao lớp 8

  50.000+
• 

  Đoạn văn nghị luận về tính tự chủ (Dàn ý + 17 Mẫu)

  100.000+
• 

  Thuyết minh về Hồ Gươm (2 Dàn ý + 13 mẫu)

  100.000+
• 

  Dẫn chứng về sự tử tế trong cuộc sống

  50.000+
• 

  36 đề thi học kì 1 môn Toán lớp 5 - Đề ôn thi học kì 1 lớp 5 môn Toán

  100.000+ 14
• 

  Dẫn chứng sống hết mình - Ví dụ về sống hết lòng, sống hết mình

  10.000+
• 

  Giải thích câu tục ngữ Đi một ngày đàng học một sàng khôn (3 Dàn ý + 28 mẫu)

  100.000+
• 

  Kết bài so sánh hai tác phẩm văn học

  10.000+
• 

  Văn mẫu lớp 11: Cảm nhận khổ 1 bài thơ Đây thôn Vĩ Dạ của Hàn Mặc Tử (3 Dàn ý + 19 Mẫu)

  100.000+ 1
• 

  Bộ đề thi học kì 2 môn Hoạt động trải nghiệm hướng nghiệp 9 sách Kết nối tri thức với cuộc sống

  1.000+

Xem thêm

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Khiếu nại & Hoàn tiền

Giải quyết vấn đề đơn hàng & hoàn trả

Mới nhất trong tuần

• Sơ đồ tư duy môn Toán 12 (Cả năm, Chương trình mới)

  

• Các dạng bài tập cực trị của hàm số

  

• Tài liệu ôn thi Toán lớp 12

  

• Bộ đề thi chọn học sinh giỏi môn Toán lớp 12 (Cấu trúc mới)

  

• Tóm tắt lý thuyết và giải nhanh Toán 12

  

• Các dạng bài tập tính đơn điệu của hàm số

  

• Đề thi thử THPT Quốc gia năm 2025 môn Ngữ văn trường THPT Yên Dũng 2, Bắc Giang

  

• 524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia

  

• Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024

  

• Lý thuyết và bài tập trắc nghiệm số phức

  

Đóng Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ Nhắn tin Zalo

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2026 download.vn.