Nguyên Lý II Nhiệt động Học | Vật Lý Đại Cương

Trang chủ » Nguyên Lý Thứ 0 » Nguyên Lý II Nhiệt động Học | Vật Lý Đại Cương

Có thể bạn quan tâm

Thư Viện Bài Giảng Vật Lý Đại CươngCùng nhau phát triển Tương lai

2.3. Nguyên lý II nhiệt động học

1. Những hạn chế của nguyên lý I

Các hiện tượng xảy ra trong tự nhiên đều tuân theo nguyên lý I nhiệt động học. Tuy nhiên, một số hiện tượng, về mặt lý thuyết, thỏa mãn nguyên lý I nhưng lại không xảy ra trong thực tế. Để minh họa điều này, ta xét 2 thí dụ sau đây:

+ Thí dụ 1: Dựa vào nguyên lý I, ta chế tạo ra một động cơ nhiệt đặt trên tầu thủy. Động cơ lấy nhiệt của nước biển để tạo công làm chạy tàu thủy. Người ta ước tính, chỉ cần hạ nhiệt độ của nước biển đi 1OC thì Đại dương sẽ cung cấp cho ta một nhiệt lượng đủ dùng cho tất cả các động cơ nhiệt trên Trái đất chạy hàng ngàn năm. Nhưng thực tế, ta không thể chế tạo ra động cơ nhiệt loại này.

Thực tế chỉ có thể tạo được động cơ nhiệt làm việc với 2 nguồn nhiệt: nhận của nguồn nóng một nhiệt lượng Q1 và trả bớt cho nguồn lạnh một nhiệt lượng Q2 đồng thời mới tạo công A.

Vậy, hệ muốn sinh công thì phải tiếp xúc với 2 nguồn nhiệt; nhiệt không thể biến hoàn toàn thành công được. Hạn chế thứ nhất của nguyên lý I là không nói đến điều này – không nói đến điều kiện chuyển hóa giữa công và nhiệt.

+ Thí dụ 2: Nguyên lý I khẳng định nhiệt có thể truyền từ vật này sang vật khác, nhưng không nói rõ từ vật nóng sang vật lạnh hay từ vật lạnh sang vật nóng. Trên thực tế, nhiệt có thể truyền từ vật nóng sang vật lạnh, nhưng không thể truyền từ vật lạnh sang vật nóng một cách tự phát được. Hạn chế thứ hai của nguyên lý I là không nói rõ chiều diễn biến trong các quá trình. Nguyên lý II của Nhiệt Động Học sẽ bổ sung, khắc phục những hạn chế trên.

Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...

  • Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
  • Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
  • Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
  • Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
  • Thời gian học từ 1,5h - 2h/1 buổi!
094.625.1920 - Thầy Nhân (Zalo)

2. Nội dụng nguyên lý II

+ Phát biểu của Clausius: Nhiệt không thể tự động truyền từ vật lạnh sang vật nóng. Nói cách khác, sự truyền nhiệt từ vật lạnh sang vật nóng không thể xảy ra nếu không có sự bù trừ nào.

+ Phát biểu của Thomson và Carnot: Không thể chế tạo được động cơ nhiệt hoạt động tuần hoàn, liên tục biến nhiệt thành công mà môi trường xung quanh không chịu sự biến đổi nào.

+ Phát biểu của Kelvin: Một hệ nhiệt động học không thể tạo công nếu chỉ tiếp xúc với một nguồn nhiệt duy nhất.

3. Quá trình thuận nghịch và quá trình không thuận nghịch

Một quá trình biến đổi của hệ nhiệt động từ trạng thái (1) đến trạng thái (2) được gọi là thuận nghịch nếu nó có thể tiến hành theo chiều ngược lại và ở lượt về (quá trình ngược), hệ đi qua tất cả các trạng thái trung gian như ở lượt đi (quá trình thuận). Trái lại là quá trình bất thuận nghịch.

Đối với quá trình thuận nghịch, nếu ở lượt đi hệ nhận công A thì ở lượt về, hệ trả đúng công A cho môi trường. Do đó, tổng công sau khi thực hiện quá trình thuận và quá trình ngược là A = 0. Mà sau khi thực hiện quá trình thuận và quá trình ngược thì hệ trở về trạng thái ban đầu nên nội năng của hệ không đổi  \( \Rightarrow dU=0\Rightarrow Q=0 \). Vậy, đối với quá trình thuận nghịch thì sau khi thực hiện quá trình thuận và quá trình ngược môi trường không bị thay đổi.

Quá trình thuận nghịch là quá trình lí tưởng (thực tế không xảy ra). Tuy nhiên, kết quả nghiên cứu đối với quá trình thuận nghịch sẽ được suy rộng cho quá trình bất thuận nghịch.

4. Hiệu suất động cơ nhiệt – Định lí Carnot

Động cơ nhiệt là một máy (thiết bị) biến nhiệt thành công.

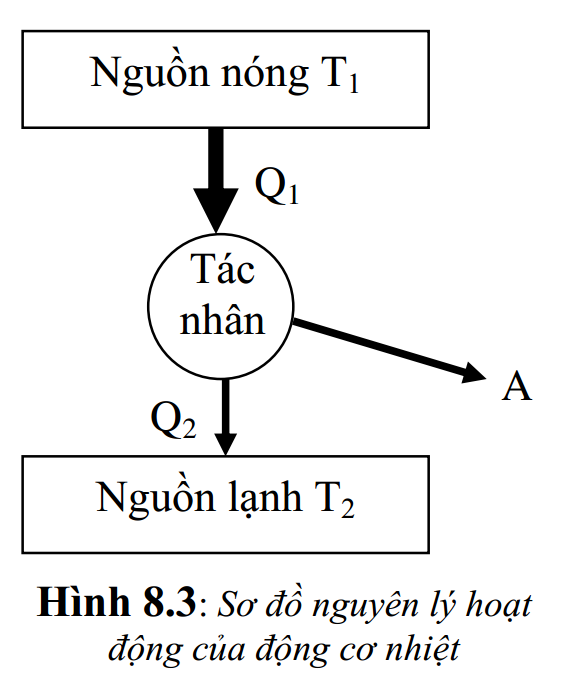
Sơ đồ nguyên lý hoạt động được mô tả ở hình 8.3: gồm 2 nguồn nhiệt (nguồn nóng T1 và nguồn lạnh T2) và một môi trường nhiệt động làm nhiệt vụ biến nhiệt thành công – ta gọi môi trường này là “tác nhận” hay “chất môi”.

Khi động cơ hoạt động, nguồn nóng T1 truyền cho chất môi một nhiệt lượng Q1. Chất môi sẽ giãn nở và sinh công A rồi trả cho nguồn lạnh một nhiệt lượng Q2.

Như vậy, hiệu suất của động cơ nhiệt là:

 \( H=\frac{\left| A \right|}{{{Q}_{1}}}=\frac{{{Q}_{1}}-\left| {{Q}_{2}} \right|}{{{Q}_{1}}}=1-\frac{\left| {{Q}_{2}} \right|}{{{Q}_{1}}}=1+\frac{{{Q}_{2}}}{{{Q}_{1}}} \)     (8.28)

Chú ý theo quy ước:  \( A,{{Q}_{2}}<0 \) vì là nhiệt lượng khí cung cấp ra bên ngoài.

Đa số các động cơ nhiệt hoạt động tuần hoàn theo những chu trình. Chu trình có lợi nhất (lí tưởng) là chu trình Carnot (do Sadi Carnot, kỹ sư người Pháp, đưa ra năm 1824). Đây là một chu trình thuận nghịch.

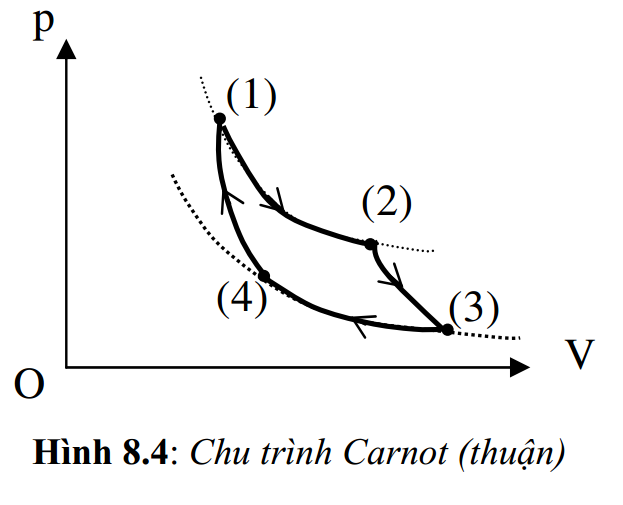
Chu trình Carnot: Gồm 4 quá trình liên tiếp:

+ Quá trình biến đổi đẳng nhiệt: Hệ nhận của nguồn nóng T1 một nhiệt lượng Q1 để giãn khí từ trạng thái (1) đến trạng thái (2), đồng thời cung cấp cho môi trường ngoài một công A1.

+ Quá trình giãn khí đoạn nhiệt: Hệ tiếp tục biến đổi đoạn nhiệt từ nhiệt độ T1 sang T2 và cung cấp cho môi trường ngoài công A2.

+ Quá trình nén khí đẳng nhiệt: Hệ nhận công A3, nén khí từ trạng thái (3) về (4) và trả cho nguồn lạnh T2 một nhiệt lượng Q2.

+ Quá trình nén khí đoạn nhiệt: Hệ tiếp tục nhận công A4, nén khí từ trạng thái (4) về trạng thái đầu (1).

Đối với chu trình Carnot, kết hợp (8.24) và phương trình trạng thái khí lí tưởng trong các giai đoạn đẳng nhiệt, ta chứng minh được:  \( \frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{V}_{3}}}{{{V}_{4}}} \)     (8.29)

(8.29) gọi là điều kiện khép kín của chu trình Carnot.

Định lí Carnot:

+ Hiệu suất của các động cơ nhiệt chạy theo chu trình không thuận nghịch thì luôn nhỏ hơn hiệu suất của động cơ nhiệt chạy theo chu trình thuận nghịch.

+ Hiệu suất của động cơ nhiệt chạy theo chu trình Carnot không phụ thuộc vào tác nhân, chỉ phụ thuộc vào nhiệt độ của các nguồn nhiệt theo biểu thức:  \( H=1-\frac{{{T}_{2}}}{{{T}_{1}}} \)       (8.30)

Thật vậy, công của khí sau một chu trình:  \( A={{A}_{12}}+{{A}_{23}}+{{A}_{34}}+{{A}_{41}} \)

Với:  \( {{A}_{12}}=\frac{m}{\mu }R{{T}_{1}}\ln \left( \frac{{{V}_{1}}}{{{V}_{2}}} \right) \); \( {{A}_{23}}=\frac{\frac{m}{\mu }R}{\gamma -1}\left( {{T}_{2}}-{{T}_{1}} \right) \); \( {{A}_{34}}=\frac{m}{\mu }R{{T}_{2}}\ln \left( \frac{{{V}_{3}}}{{{V}_{4}}} \right) \);  \( {{A}_{23}}=\frac{\frac{m}{\mu }R}{\gamma -1}\left( {{T}_{1}}-{{T}_{2}} \right) \)

Do đó:  \( A=\frac{m}{\mu }R{{T}_{1}}\ln \left( \frac{{{V}_{1}}}{{{V}_{2}}} \right)+\frac{m}{\mu }R{{T}_{2}}\ln \left( \frac{{{V}_{3}}}{{{V}_{4}}} \right) \)

Từ điều kiện khép kín (8.29) suy ra  \( \ln \left( \frac{{{V}_{3}}}{{{V}_{4}}} \right)=-\ln \left( \frac{{{V}_{1}}}{{{V}_{2}}} \right) \)

Suy ra:  \( A=\frac{m}{\mu }R\ln \left( \frac{{{V}_{1}}}{{{V}_{2}}} \right)\left( {{T}_{1}}-{{T}_{2}} \right)<0 \)

Điều này chứng tỏ sau một chu trình, khí cung cấp ra bên ngoài một công:

 \( \left| A \right|=\frac{m}{\mu }R\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\left( {{T}_{1}}-{{T}_{2}} \right) \)

Mà nhiệt lượng khí nhận được từ nguồn nóng ở giai đoạn giãn nở đẳng nhiệt là Q1.

Theo (8.22), ta có:  \( {{Q}_{1}}=-{{A}_{1}}=-\frac{m}{\mu }R{{T}_{1}}\ln \left( \frac{{{V}_{1}}}{{{V}_{2}}} \right)=\frac{m}{\mu }R{{T}_{1}}\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right) \)

Vậy hiệu suất của động cơ nhiệt chạy theo chu trình Carnot là:

 \( H=\frac{\left| A \right|}{{{Q}_{1}}}=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{1}}}=1-\frac{{{T}_{2}}}{{{T}_{1}}} \)   (điều phải chứng minh)

Từ định lí Carnot, ta rút ra nhận xét: trên thực tế, muốn tăng hiệu suất của động cơ nhiệt, ta phải tăng nhiệt độ của nguồn nóng và giảm nhiệt độ của nguồn lạnh; ngoài ra phải giảm bớt các mất mát về nhiệt để nó chạy theo chu trình gần với chu trình thuận nghịch.

5. Hệ số làm lạnh

Máy làm lạnh là thiết bị biến công thành nhiệt. Máy làm lạnh và động cơ nhiệt được gọi chung là Máy Nhiệt.

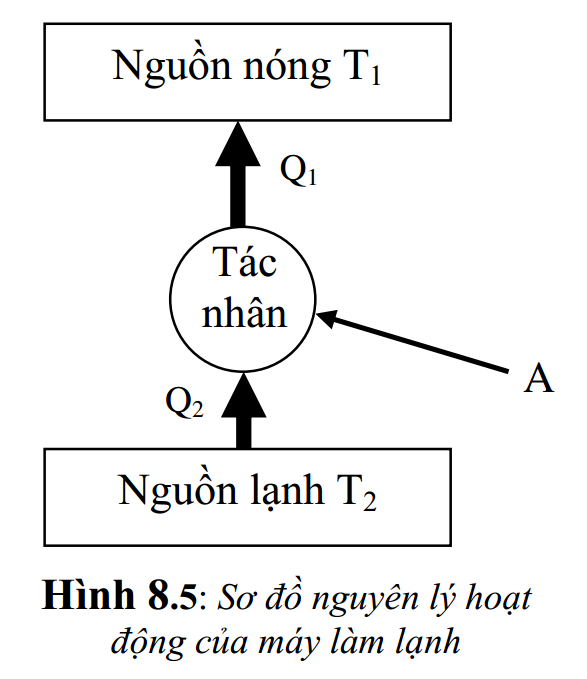
Sơ đồ nguyên lý hoạt động của máy lành lạnh được mô tả ở hình 8.5. Đầu tiên tác nhân nhận của môi trường ngoài một công A để lấy đi từ nguồn lạnh một nhiệt lượng Q2; sau đó trả cho nguồn nóng một nhiệt lượng Q1. Ta định nghĩa hệ số làm lạnh là:  \( \varepsilon =\frac{\left| {{Q}_{2}} \right|}{A} \)      (8.31)

(đôi khi người ta cũng gọi 8.31 là hiệu suất làm lạnh).

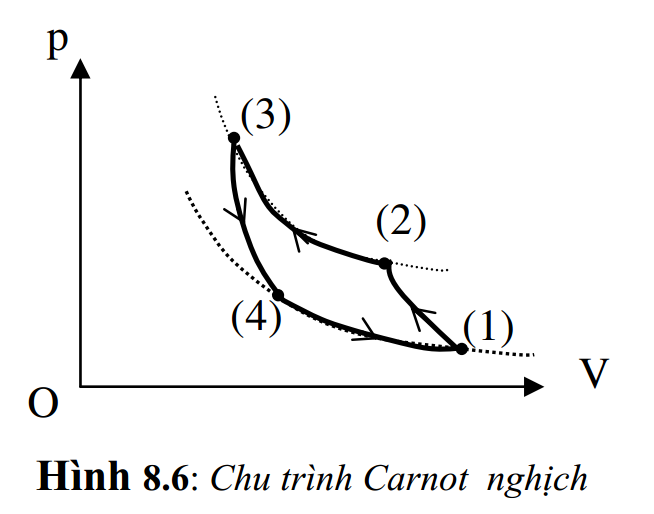
Máy làm lạnh cũng làm việc tuần hoàn, tuân theo một chu trình nhất định. Chu trình có lợi nhất là chu trình Carnot nghịch. Ở động cơ nhiệt, ta có chu trình Carnot thuận; bây giờ ta cho chu trình ấy chạy theo chiều ngược lại thì ta có chu trình Carnot nghịch. Đây chính là chu trình làm việc của máy lạnh. Nó cũng gồm 4 giai đoạn:

+ Hệ nhận công A1 để nén khí đoạn nhiệt từ trạng thái (1) sang trạng thái (2).

+ Hệ tiếp tục nhận công A2 để nén khí đẳng nhiệt từ trạng thái (2) sang trạng thái (3), đồng thời trả cho nguồn nóng nhiệt lượng Q1.

+ Giãn khí đoạn nhiệt từ trạng thái (3) sang trạng thái (4).

+ Giãn khí đẳng nhiệt từ trạng thái (4) sang trạng thái (1), đồng thời nhận của nguồn lạnh nhiệt lượng Q2 kết thúc một chu trình.

Đối với máy làm lạnh chạy theo chu trình Carnot, tương tự, ta cũng chứng minh được hệ số làm lạnh của máy không phụ thuộc vào tác nhân, chỉ phụ thuộc vào nhiệt độ của nguồn nóng và nguồn lạnh:  \( \varepsilon =\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}} \)    (8.32)

Vậy, máy nhiệt hoạt động theo chu trình Carnot là một máy thuận nghịch. Hiệu suất của các máy thuận nghịch chỉ phụ thuộc vào nhiệt độ của nguồn nóng và nguồn lạnh.

6. Biểu thức định lượng của nguyên lý II

Từ (8.28) và (8.30) ta có:  \( H=1+\frac{{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{T}_{2}}}{{{T}_{1}}} \)

Suy ra:  \( \frac{{{Q}_{2}}}{{{Q}_{1}}}=-\frac{{{T}_{2}}}{{{T}_{1}}}\Rightarrow \frac{{{Q}_{1}}}{{{T}_{1}}}+\frac{{{Q}_{2}}}{{{T}_{2}}}=0 \)

Gọi  \( \frac{Q}{T} \) là nhiệt lượng rút gọn, ta có:  \( \sum{\frac{{{Q}_{i}}}{{{T}_{i}}}}=0 \)      (8.33)

Vậy, một động cơ nhiệt chạy theo chu trình Carnot thuận nghịch thì tổng nhiệt lượng rút gọn trong một chu trình sẽ bằng không.

Đối với động cơ bất thuận nghịch thì hiệu suất luôn nhỏ hơn động cơ thuận nghịch, ta có:  \( H=1+\frac{{{Q}_{2}}}{{{Q}_{1}}}<1-\frac{{{T}_{2}}}{{{T}_{1}}} \)

 \( \Rightarrow \frac{{{Q}_{2}}}{{{Q}_{1}}}<-\frac{{{T}_{2}}}{{{T}_{1}}}\Rightarrow \frac{{{Q}_{1}}}{{{T}_{1}}}+\frac{{{Q}_{2}}}{{{T}_{2}}}<0 \) hay  \( \sum{\frac{{{Q}_{i}}}{{{T}_{i}}}}<0 \)      (8.34)

Tổng quát đối với một chu trình bất kì, ta có thể coi hệ tiếp xúc với vô số nguồn nhiệt có nhiệt độ T biến thiên liên tục; mỗi quá trình tiếp xúc với một nguồn nhiệt là một quá trình vi phân, hệ nhân nhiệt  \( \delta Q  \). Khi đó các công thức (8.33) và (8.34) trở thành tích phân kín: \(\oint{\frac{\delta Q}{T}\le 0}\)      (8.35)

Tổng nhiệt lượng rút gọn trong một chu trình biến đổi bất kì của một hệ nhiệt động không thể lớn hơn không.

Biểu thức (8.35) được gọi là bất đẳng thức Clausius – đó chính là biểu thức định lượng của nguyên lý II. Trong đó, dấu “=” ứng với chu trình thuận nghịch.

7. Entropy

a) Khái niệm Entropy

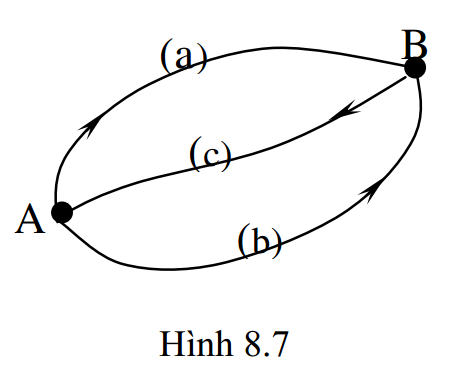
Xét quá trình biến đổi thuận nghịch của một hệ nhiệt động từ trạng thái đầu A sang trạng thái cuối B theo nhiều đường khác nhau, giả sử đường A-a-B và đường A-b-B (hình 8.7).

Để áp dụng được bất đẳng thức Clausius, ta tưởng tượng có một đường thứ ba đưa hệ từ trạng thái cuối B về trạng thái đầu A. Thế thì:

+ Đối với chu trình (A-a-B-c-A), ta có:  \( \oint{\frac{\delta Q}{T}}=0 \) hay  \( \int\limits_{A}^{B}{\frac{\delta {{Q}_{a}}}{T}}+\int\limits_{B}^{A}{\frac{\delta {{Q}_{c}}}{T}}=0 \)     (*)

+ Đối với chu trình (A-b-B-c-A), ta có:  \( \oint{\frac{\delta Q}{T}}=0 \) hay  \( \int\limits_{A}^{B}{\frac{\delta {{Q}_{b}}}{T}}+\int\limits_{B}^{A}{\frac{\delta {{Q}_{c}}}{T}}=0 \)     (**)

Vì các con đường A – a – B, A – b – B là bất kì nên từ (*) và (**) suy ra:  \( \int\limits_{A}^{B}{\frac{\delta {{Q}_{a}}}{T}}=\int\limits_{A}^{B}{\frac{\delta {{Q}_{b}}}{T}}=const  \)

Hệ thức (8.36) chứng tỏ tổng nhiệt lượng rút gọn của hệ trong quá trình biến đổi thuận nghịch từ trạng thái này sang trạng thái không phụ thuộc vào đường biến đổi hay quá trình biến đổi, mà chỉ phụ thuộc vào trạng thái đầu và trạng thái cuối. Đó là tính chất THẾ của các quá trình nhiệt động. Từ đó ta có thể tìm được một hàm thế S, gọi là hàm trạng thái hay entropy, sao cho:

\(\int\limits_{A}^{B}{\frac{\delta Q}{T}}=S(B)-S(A)=\Delta S\) hay \(dS=\frac{\delta Q}{T}\)      (8.37)

b) Các tính chất của entropy

+ Entropy là hàm đặc trưng cho trường hợp của hệ, không phụ thuộc vào quá trình biến đổi của hệ từ trạng thái này sang trạng thái khác. Trong hệ SI, entropy có đơn vị là jun trên kelvin (J/K).

+ Entropy có tính cộng được.

+ Entropy không xác định đơn giác mà sai kém một hằng số cộng:  \( S={{S}_{O}}+\int{\frac{\delta Q}{T}} \)     (8.38)

Trong đó SO là giá trị entropy tại trạng thái gốc; quy ước SO = 0 tại trạng thái T = 0 (K). Khi đó S sẽ đơn trị.

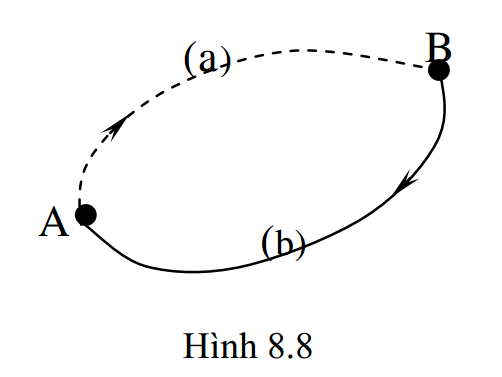
Với khái niệm entropy, ta có thể viết biểu thức định lượng của nguyên lý II dưới dạng khác. Xét một chu trình bất thuận nghịch gồm hai quá trình biến đổi (biểu diễn trên sơ đồ hình 8.8): quá trình A – a – B là quá trình bất thuận nghịch, quá trình B – b – A là quá trình thuận nghịch. Theo (8.35), ta có: \(\oint{\frac{\delta Q}{T}}<0\). Chia tích phân kín này thành tổng hai tích phân theo hai quá trình:  \( \int\limits_{(A-a-B)}{\frac{\delta Q}{T}}+\int\limits_{(B-b-A)}{\frac{\delta Q}{T}}<0 \)

Vì quá trình (B – b – A) là quá trình thuận nghịch, nên khit iến hành theo chiều ngược lại, ta có:  \( \int\limits_{(B-b-A)}{\frac{\delta Q}{T}}=-\int\limits_{(A-b-B)}{\frac{\delta Q}{T}} \)

Do đó:  \( \int\limits_{(A-a-B)}{\frac{\delta Q}{T}}-\int\limits_{(A-b-B)}{\frac{\delta Q}{T}}<0\Rightarrow \int\limits_{(A-a-B)}{\frac{\delta Q}{T}}<\int\limits_{(A-b-B)}{\frac{\delta Q}{T}} \)

Mà quá trình (A – b – B) là thuận nghịch, nên theo (8.37), ta có:

 \( \int\limits_{(A-b-B)}{\frac{\delta Q}{T}}=S(B)-S(A)=\Delta S  \)

Vậy:  \( \int\limits_{(A-a-B)}{\frac{\delta Q}{T}}<\Delta S  \) hay ở dạng vi phân:  \( \frac{\delta Q}{T}<dS  \)      (8.39)

Tổng nhiệt lượng rút gọn trong quá trình biến đổi bất thuận nghịch luôn nhỏ hơn độ biến thiên entropy.

Kết hợp (8.39) và (8.37) suy ra, đối với một quá trình biến đổi bất kì thì:  \( \Delta S\ge \int\limits_{(A)}^{(B)}{\frac{\delta Q}{T}} \) hay ở dạng vi phân:  \( dS\ge \frac{\delta Q}{T}\)       (8.40)

(8.40) chính là dạng thứ hai của biểu thức định lượng của nguyên lý II, trong đó dấu “=” ứng với quá trình thuận nghịch.

c) Nguyên lý tăng entropy

Trong một hệ cô lập (không trao đổi nhiệt với môi trường bên ngoài), ta có:

 \( \delta Q=0\Rightarrow \Delta S\ge 0 \)    (8.41)

Với quá trình thuận nghịch:  \( \Delta S=0 \)  \( \Rightarrow  \) Entropy của hệ không đổi.

Thực tế, các quá trình nhiệt động đều không thuận nghịch nên  \( \Delta S>0 \). Vậy entropy luôn tăng. Ta có nguyên lý tăng entropy: “Trên thực tế, mọi quá trình nhiệt động xảy ra trong một hệ cô lập luôn theo chiều hướng sao cho entropy của hệ tăng lên”.

Từ nguyên lý tăng entropy suy ra:

+ Một hệ cô lập không thể 2 lần cùng đi qua một trạng thái (vì nếu vậy, giá trị S sẽ trở lại giá trị ban đầu).

+ Khi hệ ở trạng thái cân bằng, sẽ kết thúc mọi quá trình biến đổi. Khi đó giá trị S đạt cực đại. Vậy, một hệ cô lập ở trạng thái cân bằng khi entropy của nó cực đại.

d) Ý nghĩa thống kê của entropy và nguyên lý II

+ Nguyên lý II cho thấy: nhiệt không thể tự động truyền từ vật lạnh sang vật nóng và entropy của hệ cô lập không thể giảm. Nói cách khác, hệ luôn có xu hướng biến đổi từ trạng thái không cân bằng về trạng thái cân bằng và khi về đến trạng thái cân bằng rồi, nó không thể tự động trở lại trạng thái không cân bằng được nữa.

+ Entropy là thước đo mức độ hỗn loạn của các phân tử trong hệ. Khi entropy giảm (ví dụ được làm lạnh) thì tính hỗn loạn của các phân tử cũng giảm, tính trật tự tăng lên và ngược lại.

+ Nguyên lý II chỉ áp dụng cho hệ vĩ mô gồm một số rất lớn các phân tử (khi đó ta có thể bỏ qua ảnh hưởng của những thăng giáng).

Các bài viết cùng chủ đề!

Năng lượng chuyển động nhiệt – Nội năng – Nhiệt lượng và công của khối khí

Xem Chi Tiết

Nguyên lý I nhiệt động học

Xem Chi Tiết

Nguyên lý II nhiệt động học

Xem Chi Tiết

Hotline: 094.625.1920 - Thầy Nhân (Zalo)

Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!

Sách Giải Bài Tập Vật Lý Đại Cương 1

Xem Chi Tiết!

Sách Giải Bài Tập Vật Lý Đại Cương 2

Xem Chi Tiết!

Sách Giải Bài Tập Vật Lý Đại Cương 3

Xem Chi Tiết!

Sách Giải Bài Tập Cơ Học Kỹ Thuật

Xem Chi Tiết!

Sách Giải Bài Tập Sức Bền Vật Liệu

Xem Chi Tiết!

University Physics – Mechanics Part 1

Xem Chi Tiết!

University Physics – Mechanics Part 2

Xem Chi Tiết!

University Physics – Electricity and Magnetism

Xem Chi Tiết!

University Physics – Waves and Thermodynamics

Xem Chi Tiết!

University Physics – Optics and Modern Physics

Xem Chi Tiết!

Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress

error: Content is protected !! MENUTrang Chủ
  • p>

Từ khóa » Nguyên Lý Thứ 0