Những Kiến Thức Về đạo Hàm Căn Cơ Bản Mà Học Sinh Nên Biết

Trang chủ » Ct đạo Hàm Căn Bậc 3 » Những Kiến Thức Về đạo Hàm Căn Cơ Bản Mà Học Sinh Nên Biết

Có thể bạn quan tâm

x

Đăng ký nhận tư vấn về sản phẩm và lộ trình học phù hợp cho con ngay hôm nay!

*Vui lòng kiểm tra lại họ tên *Vui lòng kiểm tra lại SĐT *Vui lòng kiểm tra lại Email Học tiếng Anh cơ bản (0-6 tuổi) Nâng cao 4 kỹ năng tiếng Anh (3-11 tuổi) Học Toán theo chương trình GDPT Học Tiếng Việt theo chương trình GDPT *Bạn chưa chọn mục nào! Đăng Ký Ngay X

ĐĂNG KÝ NHẬN TƯ VẤN THÀNH CÔNG!

Monkey sẽ liên hệ ba mẹ để tư vấn trong thời gian sớm nhất! Hoàn thành X

ĐÃ CÓ LỖI XẢY RA!

Ba mẹ vui lòng thử lại nhé! Hoàn thành X Bé học tiếng Anh dễ dàng cùng Monkey Junior Nhận tư vấn về chương trình Hết hạn sau 00 Ngày 00 Giờ 00 Phút 00 Giây *Vui lòng kiểm tra lại họ tên *Vui lòng kiểm tra lại SĐT Bạn là phụ huynh hay học sinh ? Học sinh Phụ huynh *Vui lòng chọn vai trò *Bạn chưa chọn mục nào! Nhận tư vấn miễn phí x

Đăng ký nhận bản tin mỗi khi nội dung bài viết này được cập nhật

*Vui lòng kiểm tra lại Email Đăng Ký
  1. Trang chủ
  2. Ba mẹ cần biết
  3. Giáo dục
  4. Kiến thức cơ bản
Đạo hàm căn: Khái niệm, công thức, dạng toán và cách giải Kiến thức cơ bản Đạo hàm căn: Khái niệm, công thức, dạng toán và cách giải Tham vấn bài viết: Hoàng Mỹ Hạnh Hoàng Mỹ Hạnh

Thạc sĩ Ngôn ngữ - Chuyên gia Giáo dục sớm

Tác giả: Ngân Hà

Ngày cập nhật: 28/10/2025

Nội dung chính

Đạo hàm căn là một trong những dạng đạo hàm cơ bản mà các em sẽ học trong chương trình toán 11. Kiến thức này thường xuất hiện trong hệ thống bài tập, đề thi và là nền tảng để học kiến thức đạo hàm nâng cao.

Video bài giảng được tạo bởi notebooklm.google.com

Đạo hàm căn là gì?

Đạo hàm được định nghĩa là tỉ số giữa số gia của hàm số cùng với số gia của một đối số tại điểm x0.

Giá trị của đạo hàm được thể hiện qua chiều biến thiên hàm số cùng độ lớn của biến thiên này.

Đạo hàm mang ý nghĩa về hình học và cả vật lý.

Đọc qua định nghĩa thì có vẻ khá trừu tượng, chúng ta có thể đơn giản hóa qua công thư như sau. Lấy một hàm số y = f(x) được xác định trên khoảng (a;b) vời x0 ∈ (a;b). Thì ta có giới hạn hữu tỉ của tỉ số khi x → x0 được gọi là đạo hàm của một hàm số đã được cho trước tại x0.

Ký hiệu của đạo hàm sẽ là: f’(x0) hay y’(x0).

Cuối cùng ta sẽ thu được: Trong đó xác định:

  • Số gia đối của △x = x - x0

  • Số gia đối của △y = y - y0

Trên đây là những kiến thức về đạo hàm và định nghĩa của đạo hàm căn thức xuất phát từ đạo hàm mà ra.

Ta tính đạo hàm căn như sau:

Áp dụng công thức tính đạo hàm ta có:

Với hàm số y = (căn u) ta có đạo hàm y' = ( căn u)'= u'/2(căn u).

Đây chính là công thức tổng quát và được áp dụng cho hầu hết những bài toán tính căn đạo hàm.

Đạo hàm căn là kiến thức cơ bản mà các bạn học sinh nên nhớ. (Sưu tầm Internet)

Các công thức về đạo hàm căn cần biết

Đạo hàm căn không hề đơn giản và cần khoảng thời gian tìm hiểu, luyện tập nhiều thì mới tiến bộ và nắm vững kiến thức được. Để rút ngắn thời gian tính toán, Monkey sẽ giới thiệu cho bạn những công thức về đạo hàm căn đơn giản mà ai cũng nên biết dưới đây:

  • Đối với những căn thức đơn giản, ta có công thức: , đây là công thức mà ai cũng nên nhớ.

  • Công thức tổng quát đạo hàm căn bậc 2 của u, ta có công thức:

  • Đối với những bài toán chứa căn bậc 2 có u dưới mẫu, ta có công thức:

  • Đối với những bài toán đạo hàm căn u bậc n, ta có công thức tổng quát:

Trên đây là một số công thức cơ bản về đạo hàm mà ai cũng nên biết và học thuộc để quá trình tính toán diễn ra dễ dàng hơn.

Bảng công thức về đạo hàm mà ai cũng cần phải biết. (Sưu tầm Internet)

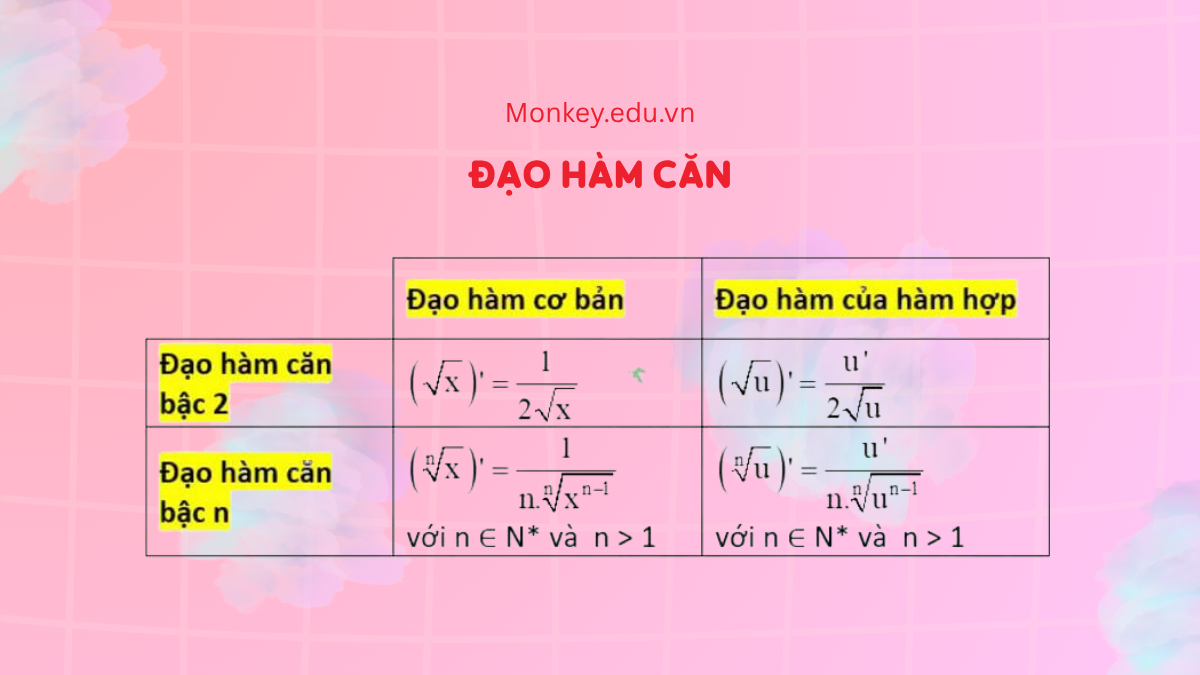
1. Công thức tính chung cho đạo hàm căn thức

Tuy có nhiều công thức đạo hàm căn khác nhau, tuy nhiên công thức chung và tổng quát về đạo hàm căn thức chính là:

  • Đối với đạo hàm căn x bậc n: với n ∈ N*, n > 1

  • Đối với đạo hàm căn u bậc n: với n ∈ N*, n > 1

Đây là hai công thức bao quát nhất và hầu như có thể áp dụng cho các dạng bài toán tính căn khác nhau, tùy thuộc vào nhu cầu sử dụng. Những bạn học sinh cần ghi nhớ rõ công thức này.

Một số bài toán cụ thể như sau:

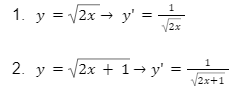
2. Công tính đạo hàm căn bậc 2

Công thức tổng quát:

Ví dụ: Tính đạo hàm của hàm số: y = 2(căn x)

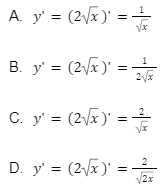
Đáp án: A

Có nhiều dạng bài đạo hàm căn khác nhau và các bạn học sinh cần ghi nhớ. (Sưu tầm Internet)

3. Công tính đạo hàm căn bậc 3

Công thức tổng quát:

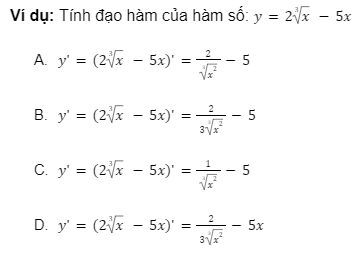
Đáp án: B

4. Công tính đạo hàm căn bậc 4

Công thức tổng quát:

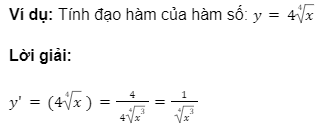
5. Công tính đạo hàm căn u

Công thức tổng quát: Đối với đạo hàm căn u bậc n, ta có: với n ∈ N*, n > 1

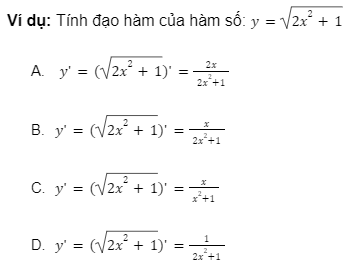
Đáp án: A

Công thức tính đạo hàm căn cơ bản mà các bạn học sinh nên nhớ. (Sưu tầm Internet)

6. Công tính đạo hàm căn x

Công thức tổng quát: Đối với đạo hàm căn x bậc n, ta có: với n ∈ N*, n > 1

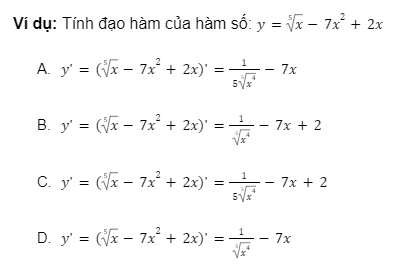
Đáp án: C

7. Công thức tính đạo hàm căn logarit

Đối với đạo hàm logarit căn x

Công thức tổng quát:

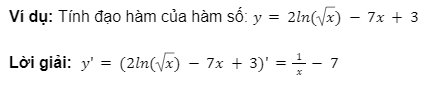
Đối với đạo hàm logarit căn u

GIÚP CON HỌC TOÁN KẾT HỢP VỚI TIẾNG ANH SIÊU TIẾT KIỆM CHỈ TRÊN MỘT APP MONKEY MATH. VỚI NỘI DUNG DẠY HỌC ĐA PHƯƠNG PHÁP GIÚP BÉ PHÁT TRIỂN TƯ DUY NÃO BỘ VÀ NGÔN NGỮ TOÀN DIỆN CHỈ VỚI KHOẢNG 2K/NGÀY.

Các dạng bài tập đạo hàm căn tự luyện (có lời giải)

Đạo hàm căn là có rất nhiều dạng bài tập vô cùng đa dạng, đòi hỏi các bạn học sinh phải nắm rõ bản chất. Dưới đây, Monkey sẽ giới thiệu một số mẫu bài tập tự luyện có lời giải phổ biến nhất hiện nay, cùng tìm hiểu nhé!

Dạng 1: Bài tập tính đạo hàm của những hàm số

Ví dụ: Tính đạo hàm của những hàm số sau

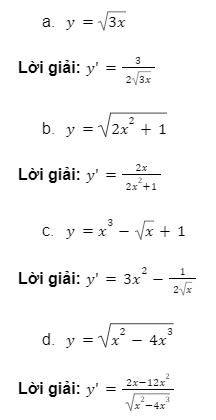
Dạng 2: Bài tập tìm x để theo điều kiện của y’

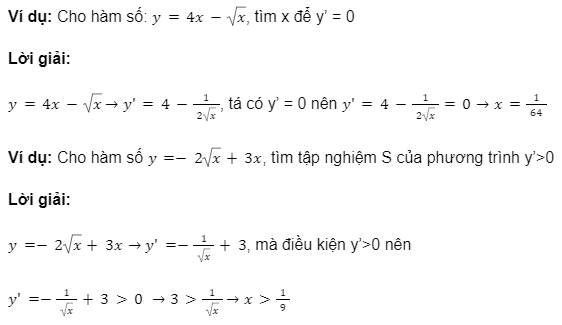
Đạo hàm căn là có rất nhiều dạng bài tập vô cùng đa dạng. (Sưu tầm Internet)

Dạng 3: Tình đạo hàm của hàm số tại một điểm x = a

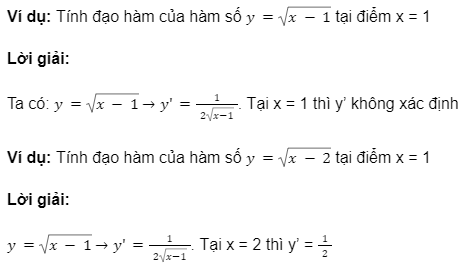
Trên đây là một số dạng toán cơ bản về đạo hàm căn mà các bạn học sinh có thể tham khảo để củng cố những công thức được nêu ra ở trên.

Các bài viết không thể bỏ lỡ \displaystyle

Monkey Math - Ứng dụng học toán tiếng Anh chỉ với 2K/Ngày

\displaystyle

Gợi ý công thức đạo hàm nhanh giúp tính toán nhanh chóng, dễ dàng và chính xác nhất

\displaystyle

Đạo hàm và ứng dụng của đạo hàm trong thực tiễn có gì thú vị?

Bài tập đạo hàm căn tự luyện (có đáp án)

>>> Tải bài tập đạo hàm của thầy Trần Sĩ Tùng ngay tại đây!

(Nguồn: Tổng hợp)

FAQ - Những thắc mắc khác về đạo hàm căn trong toán học

1. Tại sao lại có u′ (x) ở trên tử số?

Vì đây là quy tắc đạo hàm hàm hợp. Khi bạn có một 'hàm bên trong' [là u(x) nằm dưới dấu căn] và một 'hàm bên ngoài' (là hàm căn bậc hai), bạn phải lấy đạo hàm của hàm bên ngoài rồi nhân với đạo hàm của hàm bên trong.

2. Đạo hàm của hàm số chứa căn có phải lúc nào cũng dương không?

Không. Dấu của đạo hàm phụ thuộc vào dấu của đạo hàm của 'hàm bên trong' u(x).

3. Đạo hàm căn có ứng dụng gì trong thực tế?

Đạo hàm căn cũng có ứng dụng rộng rãi giống như các loại đạo hàm khác. Nó giúp bạn tìm tốc độ thay đổi tức thời trong các mô hình vật lý, kinh tế và kỹ thuật.

Ví dụ, nó có thể được dùng để:

  • Tính tốc độ của một vật thể rơi tự do theo công thức v=2gh​.
  • Tối ưu hóa các bài toán về chi phí trong kinh tế khi hàm chi phí được biểu diễn dưới dạng căn thức.
  • Trong hình học, nó có thể được sử dụng để tìm độ dốc của tiếp tuyến tại một điểm trên đường cong được mô tả bởi một hàm căn.

Qua những thông tin mà Monkey cung cấp ở trên, hy vọng những bạn học sinh đã nắm được phần nào những kiến thức cơ bản về đạo hàm của căn. Đây là một vùng kiến thức rất rộng và đòi hỏi phải có sự chăm chỉ rèn luyện. Chúc các bạn học sinh sẽ nắm vững và thành thạo về đạo hàm căn nhé!

Nguồn tham khảo

1. SGK Kết nối tri thức - Toán 11 - Bài 32: Các quy tắc tính đạo hàm (Tham khảo ngày 28/10/25)

2. SGK Kết nối tri thức - Toán 12 - Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn (Tham khảo ngày 28/10/25)

3. SGK Cánh Diều - Toán 11 - Chương 7 - Bài 2: Các quy tắc tính đạo hàm (Tham khảo ngày 28/10/25)

Chia sẻ ngay button-share Chia sẻ

Sao chép liên kết

Thông tin trong bài viết được tổng hợp nhằm mục đích tham khảo và có thể thay đổi mà không cần báo trước. Quý khách vui lòng kiểm tra lại qua các kênh chính thức hoặc liên hệ trực tiếp với đơn vị liên quan để nắm bắt tình hình thực tế.

Bài viết liên quan
  • Lý thuyết - bài tập về chuyển đổi giữa khối lượng thể tích và lượng chất
  • Nguyên hàm hàm hợp: Công thức và cách giải chi tiết
  • Oxi: Tính chất, ứng dụng và cách điều chế [Tổng hợp Lớp 8 + 10]
  • Phép cộng là gì? Tổng hợp kiến thức cơ bản nhất trong phép cộng
  • Phép chia là gì? Tổng hợp kiến thức cơ bản nhất trong phép chia
Bạn có đang quan tâm đến việc cho con học Tiếng Anh? Có Không Giúp bé giỏi Tiếng Anh Sớm Đăng ký ngay tại đây *Vui lòng kiểm tra lại họ tên *Vui lòng kiểm tra lại SĐT *Vui lòng kiểm tra lại Email Đăng ký ngay Nhận các nội dung mới nhất, hữu ích và miễn phí về kiến thức Giáo dục trong email của bạn *Vui lòng kiểm tra lại Email Đăng Ký Các Bài Viết Mới Nhất Concentrate đi với giới từ gì? Cấu trúc concentrate chuẩn ngữ pháp Concentrate đi với giới từ gì? Cấu trúc concentrate chuẩn ngữ pháp Surprised đi với giới từ gì? Cấu trúc sử dụng surprised chuẩn nhất Surprised đi với giới từ gì? Cấu trúc sử dụng surprised chuẩn nhất Prevent đi với giới từ gì? Cách dùng prevent chuẩn ngữ pháp tiếng Anh Prevent đi với giới từ gì? Cách dùng prevent chuẩn ngữ pháp tiếng Anh Sau danh từ là gì? Cách xác định loại từ phù hợp & Bài tập vận dụng (có đáp án) Sau danh từ là gì? Cách xác định loại từ phù hợp & Bài tập vận dụng (có đáp án) 100 động từ bất quy tắc thường gặp nhất trong tiếng Anh 100 động từ bất quy tắc thường gặp nhất trong tiếng Anh Concentrate đi với giới từ gì? Cấu trúc concentrate chuẩn ngữ pháp Concentrate đi với giới từ gì? Cấu trúc concentrate chuẩn ngữ pháp Surprised đi với giới từ gì? Cấu trúc sử dụng surprised chuẩn nhất Surprised đi với giới từ gì? Cấu trúc sử dụng surprised chuẩn nhất Prevent đi với giới từ gì? Cách dùng prevent chuẩn ngữ pháp tiếng Anh Prevent đi với giới từ gì? Cách dùng prevent chuẩn ngữ pháp tiếng Anh Sau danh từ là gì? Cách xác định loại từ phù hợp & Bài tập vận dụng (có đáp án) Sau danh từ là gì? Cách xác định loại từ phù hợp & Bài tập vận dụng (có đáp án) 100 động từ bất quy tắc thường gặp nhất trong tiếng Anh 100 động từ bất quy tắc thường gặp nhất trong tiếng Anh

Đăng ký tư vấn nhận ưu đãi

Monkey Junior

Mới! *Vui lòng kiểm tra lại họ tên *Vui lòng kiểm tra lại SĐT Bạn là phụ huynh hay học sinh ? Học sinh Phụ huynh *Bạn chưa chọn mục nào! Đăng Ký Mua Monkey Junior

Từ khóa » Ct đạo Hàm Căn Bậc 3