Ôn Tập Chương 2 Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Lôgarit
Có thể bạn quan tâm
1. Công thức mũ và lũy thừa
Cho a và b > 0, m và n là những số thực tùy ý, ta có các công thức mũ và lũy thừa sau:
.png)
2. Công thức lôgarit
Cho \(a<0\ne1,b>0\) và \(x,y>0,\) ta có các công thức sau:
(1).png)
Công thức đổi cơ số:
.png)
3. Đạo hàm của hàm số lũy thừa, hàm số mũ và hàm số lôgarit
.png)
4. Hàm số lũy thừa, hàm số mũ, hàm số lôgarit
a) Hàm số lũy thừa
Bảng tóm tắt các tính chất của hàm số lũy thừa \(y=x^{\alpha}\) trên khoảng \(\left( {0; + \infty } \right)\)
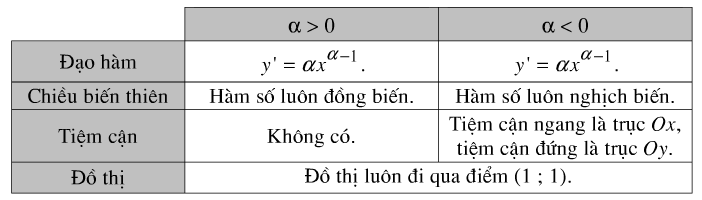
b) Hàm số mũ
Bảng tóm tắt các tính chất của hàm số mũ \(y=a^x(a>0,a\ne1)\)

c) Hàm số lôgarit
Bảng tóm tắt các tính chất của hàm số lôgarit \(y={\log_a}x(a>0,a\ne1)\)

5. Phương trình và bất phương trình mũ
Các phương pháp giải:
- Phương pháp đưa về cùng cơ số.
- Phương pháp lôgarit hóa.
- Phương pháp đặt ẩn phụ.
- Phương pháp hàm số.
6. Phương trình và bất phương trình lôgarit
Các phương pháp giải:
- Phương pháp đưa về cùng cơ số
- Phương pháp mũ hóa.
- Phương pháp đặt ẩn phụ.
- Phương pháp hàm số.
7. Bài tập minh họa
Bài tập 1:
Cho a, b, c > 0; a, b, c\(\neq\)1 thỏa mãn ac = b2. CMR: \(\log_ab+\log_cb=2\log_ab.\log_cb.\)
Lời giải:
\(ac=b^2\Rightarrow \log_b\ a+\log_b\ c=2\)\(\Rightarrow \frac{1}{\log_a \ b}+\frac{1}{\log_c \ b}=2\) \(\Rightarrow \frac{\log_c \ b +\log_a \ b}{\log_a \ b .\log_c \ b}=2\)\(\Rightarrow \log_c \ b +\log_a \ b = 2\log_a \ b . \log_c \ b\).
Bài tập 2:
Cho \(\log_{3}5=a\). Tính \(\log_{75}45\) theo a.
Lời giải:
\(\log_{75}45=\frac{\log_{3}45}{\log_{3}75}=\frac{\log_{3}(3^{2}.5)}{\log_{3}(3.5^{2})}\)\(=\frac{log_{3}3^{2}+log_{3}5}{log_{3}3+log_{3}5^{2}}=\frac{2+log_{3}5}{1+2log_{3}5}\)\(=\frac{2+a}{1+2a}\).
Bài tập 3:
Một người gửi tiết kiệm ngân hàng với lãi suất 6,8%/năm và lãi hàng năm được nhập vào vốn. Cho biết số tiền cả gốc và lãi được tính theo công thức \(T=A(1+r)^n\), trong đó A là số tiền gửi, r là lãi suất và n là số kỳ hạn gửi. Hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?Lời giải:
Sau n năm số tiền thu được là \(T=A(1+0,068)^n\) Để T = 2A thì phải có \((1,068)^n=2 \ \ (hay \ (1+6,8\%)^n=2)\) \(\Leftrightarrow n=log_{1,068}.2\approx 10,54\) Vậy muốn thu được gấp đôi số tiền ban đầu, người đó phải gửi 11 năm.Bài tập 4:
Giải phương trình \(\log_8\frac{8}{x^2}=3\log_8^2x.\)Lời giải:
Điều kiện: \(\left\{ \begin{array}{l} x > 0\\ {\log _8}\frac{8}{{{x^2}}} \ge 0 \end{array} \right. \Leftrightarrow 0 < x < 2\sqrt 2 .\) \(\log_8\frac{8}{x^2}=3\log_8^2x\Leftrightarrow \log_88 -\log_8x^2=3.\log_8^2x\) \(\Leftrightarrow 3\log_8^2x+2\log_8x^2-1=0\) Đặt \(t=\log_8x\), phương trình trở thành: \(3{t^2} + 2t - 1 = 0 \Leftrightarrow \left[ \begin{array}{l} t = - 1\\ t = \frac{1}{3} \end{array} \right.\) Với: \(t=-1\Leftrightarrow log_8x=-1\Leftrightarrow x=\frac{1}{8}\) Với: \(t=\frac{1}{3}\Leftrightarrow log_8x=\frac{1}{3}\Leftrightarrow x=2\) Vậy tập nghiệm phương trình là: \(\left \{ \frac{1}{8};2 \right \}\).Bài tập 5:
Giải bất phương trình: \(\log_{0,5}x+2\log_{0,25}(x-1)+\log_26\geq 0.\)Lời giải:
Điều kiện: x> 1 (*). Khi đó ta có: \(\log_{0,5}x+2\log_{0,25}(x-1)+\log_26\geq 0\) \(\Leftrightarrow \log_2x-\log_2(x-1)+\log_26\geq 0\) \(\Leftrightarrow \log_2[x(x-1)]\leq \log_26\Leftrightarrow x(x-1)\leq 6\Leftrightarrow x^2-x-6\leq 0\) \(\Leftrightarrow -2\leq x\leq 3\). Kết hợp điều kiện (*) ta được \(1 < x \le 3\) Vậy tập nghiệm bất phương trình là S=(1;3].Bài tập 6:
Giải phương trình \(27^x-5.3^{2-3x}=4.\)Lời giải:
\(27^x-5.3^{2-3x}=4\Leftrightarrow 27^x-\frac{45}{27^x}=4\Leftrightarrow (27^x)^2-4.27^x-45=0\) Đặt: \(t=27^x(t>0)\) ta được \(t^2-4t-45=0\)\(\Leftrightarrow t=9\) (Do t>0). \(\Rightarrow 3^{3x}=3^2\Leftrightarrow 3x=2\Leftrightarrow x=\frac{2}{3}\). Vậy phương trình đã cho có nghiệm là \(x=\frac{2}{3}\).Bài tập 7:
Giải bất phương trình \(4^x-3^x>1.\)Lời giải:
\(4^x-3^x>1\Leftrightarrow 4^x>3^x+1\)\(\Leftrightarrow 1>(\frac{3}{4})^x+(\frac{1}{4})^x\) Với \(x\leq 1\) ta có: \(\left.\begin{matrix} \left ( \frac{3}{4} \right )^x\geqslant \frac{3}{4}\\ \\ \left ( \frac{1}{4} \right )^x\geqslant \frac{1}{4} \end{matrix}\right\}VP\geqslant 1\) Không thỏa mãn. Với \(x>1\) ta có: \(\left.\begin{matrix} (\frac{3}{4})^x<\frac{3}{4}\\ \\ (\frac{1}{4})^x< \frac{1}{4} \end{matrix}\right\}VP< 1\) thỏa mãn.
Vậy bất phương trình có tập nghiệm là: \(S=(1;+\infty ).\)
Từ khóa » Hàm Số Lũy Thừa Hàm Số Mũ Hàm Số Lôgarit
-
Lý Thuyết Hàm Số Mũ, Hàm Số Logarit, Hàm Số Lũy Thừa Chi Tiết
-
Tổng ôn Toàn Bộ Hàm Số Luỹ Thừa Hàm Số Mũ Và Hàm Số Logarit
-
Hàm Số Lũy Thừa Và Hàm Số Mũ, Trắc Nghiệm Toán Học Lớp 12
-
Mũ – Logarit - Lũy Thừa
-
ÔN TẬP HÀM SỐ LŨY THỪA , MŨ , LOGARIT - TOÁN 12 - YouTube
-
Đồ Thị Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
[PDF] HÀM SỐ LŨY THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT | Hoc360.
-
Hàm Số Lũy Thừa, Hàm Số Mũ Và Logarit, Bài Tập áp Dụng - Toán 12
-
Lý Thuyết Tổng Hợp Chương Hàm Số Lũy Thừa, Hàm Số ... - Haylamdo
-
Tập Xác định Của Hàm Số Mũ Lũy Thừa Lôgarit
-
Tài Liệu Tự Học Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
Tập Xác định Của Hàm Số Mũ, Lũy Thừa, Logarit Cực đơn Giản [VD ...
-
Lý Thuyết Hàm Số Mũ, Hàm Số Lôgarit | SGK Toán Lớp 12
-
Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Lôgarit Môn Toán Lớp 12