Phân Tích đa Thức Thành Nhân Tử Bằng Phương Pháp đặt Nhân Tử ...

Home » Toán Học » Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung Toán Học Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung admin.ta 6 Tháng Một, 2026 66 Views 0 SaveSavedRemoved 0

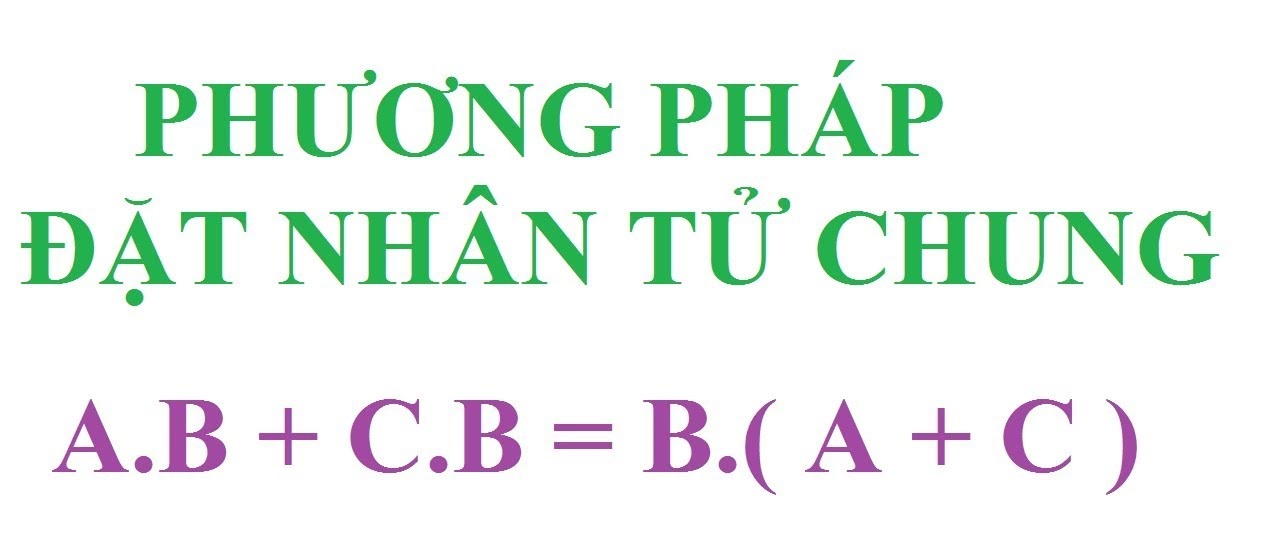
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung được sử dụng trong những trường hợp như thế nào ? Cùng theo dõi bài viết để hiểu hơn về phương pháp này nhé !

Tham khảo bài viết khác:

• Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử – Toán lớp 8
• Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

     Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Tóm tắt nội dung

• 1      Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
• 2     Bài tập có lời giải vận dụng phương pháp

– Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức. Việc phân tích đa thức thành nhân tử giúp ta có thể thu gọn biểu thức, tính nhanh và giải phương trình dễ dàng.

– Phương pháp đặt nhân tử chung

+) Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

+)  Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.

Lưu ý: Hãy nhớ thay đổi dấu trong bài khi nhóm các hạng tử

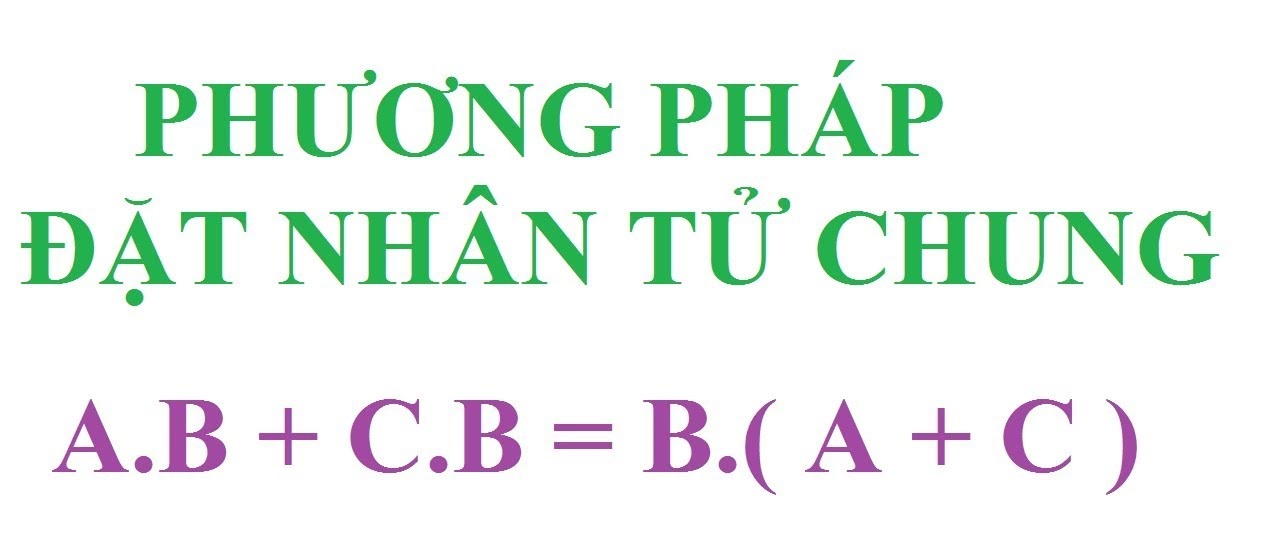
    Bài tập có lời giải vận dụng phương pháp

Bài tập 1: Phân tích các đa thức sau thành nhân tử:

a) x(x – y) – 3x + 3y

B) 10x(x – y) – 8y(y – x).

– Hướng dẫn giải:

a)

x(x – y) – 3x + 3y

= x(x – y) – 3(x – y)

= (x – y)(x – 3)

b)

10x(x – y) – 8y(y – x)

=10x(x – y) – 8y[-(x – y)]

= 10x(x – y) + 8y(x – y)

= 2(x – y)(5x + 4y)

Bài tập 2: Tìm x, biết:

a) 5x(x -2000) – x + 2000 = 0;

b) x^3 – 13x = 0

– Hướng dẫn giải:

a)

5x(x -2000) – (x – 2000) = 0

(x – 2000)(5x – 1) = 0

Hoặc 5x – 1 = 0 => 5x = 1 => x =1/5

Vậy x =1/5; x = 2000

b)

x^3 – 13x = 0

x(x2 – 13) = 0

Hoặc x = 0

Hoặc x^2 – 13 = 0 => x^2 = 13 => x = ±√13

Vậy x = 0; x = ±√13

Bài tập 3: Tính giá trị của các biểu thức:

a) 15.91,5 + 150.0,85

b) x(x – 1) – y(1 – x) tại x = 2001 và y = 1999

– Hướng dẫn giải: 

a)

15.91,5 + 150.0,85

= 15.91,5 + 15.10.0,85

= 15.91,5 + 15.8,5

= 15(91,5 + 8,5)

= 15.100

= 1500

b)

x(x – 1) – y(1 – x)

= x(x – 1) – y[–(x – 1)]

= x(x – 1) + y(x – 1)

= (x – 1)(x + y)

Tại x = 2001, y = 1999, giá trị biểu thức bằng:

(2001 – 1)(2001 + 1999) = 2000.4000 = 8000000

Hy vọng bài viết Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung sẽ đem đến cho bạn những nội dung thông tin hữu ích, hẹn gặp lại bạn ở những bài viết tiếp theo !

Người xem: 555