Phép Biến đổi Fourier Trực Tiếp Cho Phép Bạn Xác định ...

Biến đổi Fourier- đây là một họ các phương pháp toán học dựa trên sự phân rã của hàm liên tục ban đầu của thời gian thành một tập hợp các hàm điều hòa cơ bản (là các hàm hình sin) với các tần số, biên độ và pha khác nhau. Có thể thấy từ định nghĩa rằng ý tưởng chính của phép biến đổi là bất kỳ hàm nào cũng có thể được biểu diễn dưới dạng tổng vô hạn của các hình sin, mỗi hàm sẽ được đặc trưng bởi biên độ, tần số và pha ban đầu của nó.

Phép biến đổi Fourier là người sáng lập ra phép phân tích quang phổ. Phân tích phổ là một phương pháp xử lý tín hiệu cho phép bạn mô tả nội dung tần số của tín hiệu được đo. Tùy thuộc vào cách biểu diễn tín hiệu, các phép biến đổi Fourier khác nhau được sử dụng. Có một số kiểu biến đổi Fourier:

- Biến đổi Fourier liên tục (trong tài liệu tiếng Anh là Continue Time Fourier Transform - CTFT hay nói ngắn gọn là FT);

- Biến đổi Fourier rời rạc (trong tài liệu tiếng Anh Biến đổi Fourier rời rạc - DFT);

- Biến đổi Fourier nhanh (trong tài liệu tiếng Anh Phép biến đổi Fast Fourier - FFT).

Biến đổi Fourier liên tục

Phép biến đổi Fourier là một công cụ toán học được sử dụng trong các lĩnh vực khoa học khác nhau. Trong một số trường hợp, nó có thể được sử dụng như một phương tiện để giải các phương trình phức tạp mô tả các quá trình động lực học xảy ra dưới ảnh hưởng của năng lượng điện, nhiệt hoặc ánh sáng. Trong các trường hợp khác, nó cho phép bạn làm nổi bật các thành phần thông thường trong một tín hiệu dao động phức tạp, để bạn có thể diễn giải chính xác các quan sát thực nghiệm trong thiên văn, y học và hóa học. Một phép biến đổi liên tục thực chất là một phép tổng quát của chuỗi Fourier, với điều kiện là chu kỳ của hàm mở rộng có xu hướng đến vô cùng. Do đó, phép biến đổi Fourier cổ điển xử lý phổ của tín hiệu được thực hiện trên toàn bộ phạm vi tồn tại của biến.

Có một số kiểu viết một phép biến đổi Fourier liên tục, khác nhau bởi giá trị của hệ số đứng trước tích phân (hai dạng viết):

hoặc

ở đâu và là ảnh Fourier của hàm hoặc phổ tần số của hàm;

- tần số tròn.

Cần lưu ý rằng các kiểu ghi âm khác nhau được tìm thấy trong các lĩnh vực khoa học và công nghệ khác nhau. Yếu tố chuẩn hóa là cần thiết để chia tỷ lệ chính xác của tín hiệu từ miền tần số sang miền thời gian. Hệ số chuẩn hóa làm giảm biên độ của tín hiệu ở đầu ra của phép biến đổi nghịch đảo để nó phù hợp với biên độ của tín hiệu ban đầu. Trong tài liệu toán học, phép biến đổi Fourier trực tiếp và nghịch đảo được nhân với một hệ số, trong khi trong vật lý, thông thường, với một phép biến đổi trực tiếp, hệ số không được đặt, nhưng với phép nghịch đảo, thừa số được đặt. Nếu chúng ta tính toán tuần tự biến đổi Fourier trực tiếp của một tín hiệu nào đó, rồi thực hiện biến đổi Fourier ngược, thì kết quả của biến đổi nghịch đảo phải hoàn toàn trùng khớp với tín hiệu ban đầu.

Nếu hàm là số lẻ trên khoảng (−∞, + ∞), thì biến đổi Fourier có thể được biểu diễn dưới dạng hàm sin:

Nếu hàm số chẵn trên khoảng (−∞, + ∞), thì biến đổi Fourier có thể được biểu diễn theo hàm cosin:

Do đó, phép biến đổi Fourier liên tục cho phép chúng ta biểu diễn một hàm không tuần hoàn dưới dạng tích phân của một hàm biểu diễn tại mỗi điểm của nó hệ số của chuỗi Fourier đối với một hàm không tuần hoàn.

Phép biến đổi Fourier có thể đảo ngược, nghĩa là, nếu ảnh Fourier của nó được tính toán từ hàm, thì hàm ban đầu có thể được khôi phục duy nhất từ ​​ảnh Fourier. Phép biến đổi Fourier ngược được hiểu là một phép tích phân có dạng (hai dạng viết):

hoặc

đâu là ảnh Fourier của hàm hoặc phổ tần số của hàm;

- tần số tròn.

Nếu hàm là số lẻ trên khoảng (−∞, + ∞), thì biến đổi Fourier ngược có thể được biểu diễn dưới dạng hàm sin:

Nếu hàm số chẵn trên khoảng (−∞, + ∞), thì phép biến đổi Fourier ngược có thể được biểu diễn theo hàm cosin:

Ví dụ, hãy xem xét chức năng sau . Dưới đây là đồ thị của hàm số mũ đang nghiên cứu.

Vì hàm là một hàm chẵn nên phép biến đổi Fourier liên tục sẽ được định nghĩa như sau:

Kết quả là, chúng tôi thu được sự phụ thuộc của sự thay đổi trong hàm số mũ đã nghiên cứu vào khoảng tần số (xem bên dưới).

Phép biến đổi Fourier liên tục thường được sử dụng trong lý thuyết khi xem xét các tín hiệu thay đổi theo các chức năng đã cho, nhưng trong thực tế chúng thường xử lý các kết quả đo biểu thị dữ liệu rời rạc. Kết quả đo được ghi lại trong khoảng thời gian đều đặn với một tần số lấy mẫu nhất định, ví dụ, 16000 Hz hoặc 22000 Hz. Tuy nhiên, trong trường hợp chung, các phép đọc rời rạc có thể diễn ra không đồng đều, nhưng điều này làm phức tạp bộ máy phân tích toán học, vì vậy nó thường không được sử dụng trong thực tế.

Có một định lý quan trọng của Kotelnikov (trong tài liệu nước ngoài có tên là “Định lý Nyquist-Shannon”, “định lý mẫu”), trong đó nói rằng một tín hiệu tuần hoàn tương tự có phổ hữu hạn (giới hạn về chiều rộng) (0 ... fmax) có thể được khôi phục duy nhất mà không bị biến dạng và suy hao trong các số đọc rời rạc của chúng, được lấy với tần số lớn hơn hoặc bằng hai lần tần số trên của phổ - tần số lấy mẫu (fdisc> = 2 * fmax). Nói cách khác, ở tốc độ lấy mẫu 1000 Hz, tín hiệu có tần số lên đến 500 Hz có thể được phục hồi từ tín hiệu tuần hoàn tương tự. Cần lưu ý rằng sự tùy biến của một chức năng trong thời gian dẫn đến chu kỳ của phổ của nó, và sự tùy tiện của phổ về tần số dẫn đến chu kỳ của chức năng.

Đây là một trong những phép biến đổi Fourier được sử dụng rộng rãi trong các thuật toán xử lý tín hiệu số.

Phép biến đổi Fourier rời rạc trực tiếp kết hợp một hàm thời gian, được xác định bởi N điểm đo trên một khoảng thời gian nhất định, với một hàm khác, được xác định trên một khoảng tần số. Cần lưu ý rằng hàm trên khoảng thời gian được chỉ định bằng cách sử dụng N mẫu, và hàm trên miền tần số được chỉ định bằng phổ K-lần.

k ˗ chỉ số tần số.

Tần số của tín hiệu thứ k được xác định bằng biểu thức

trong đó T là khoảng thời gian dữ liệu đầu vào được lấy.

Phép biến đổi rời rạc trực tiếp có thể được viết lại theo các thành phần thực và ảo. Thành phần thực là một mảng chứa các giá trị của các thành phần sin và thành phần ảo là một mảng chứa các giá trị của các thành phần sin.

Từ các biểu thức cuối cùng có thể thấy rằng sự biến đổi phân hủy tín hiệu thành các thành phần hình sin (được gọi là sóng hài) với tần số từ một dao động trong một chu kỳ đến N dao động trong một chu kỳ.

Biến đổi Fourier rời rạc có một đặc điểm, vì một chuỗi rời rạc có thể thu được bằng tổng các hàm có thành phần khác nhau của tín hiệu hài. Nói cách khác, một chuỗi rời rạc được phân tách thành các biến hài hòa - một cách mơ hồ. Do đó, khi phân rã một hàm rời rạc bằng cách sử dụng biến đổi Fourier rời rạc, các thành phần tần số cao xuất hiện trong nửa sau của phổ, không có trong tín hiệu ban đầu. Phổ tần số cao này là hình ảnh phản chiếu của phần đầu tiên của phổ (về tần số, pha và biên độ). Thường thì nửa sau của quang phổ không được xem xét, và các biên độ tín hiệu của phần đầu tiên của phổ được tăng gấp đôi.

Cần lưu ý rằng sự mở rộng của một hàm liên tục không dẫn đến sự xuất hiện của hiệu ứng phản chiếu, vì một hàm liên tục được phân tích duy nhất thành các biến điều hòa.

Biên độ của thành phần DC là giá trị trung bình của hàm trong một khoảng thời gian đã chọn và được xác định như sau:

Biên độ và pha của các thành phần tần số của tín hiệu được xác định theo các mối quan hệ sau:

Các giá trị biên độ và pha kết quả được gọi là ký hiệu cực. Vectơ tín hiệu thu được sẽ được xác định như sau:

Xem xét thuật toán biến đổi một hàm riêng biệt đã cho trên một khoảng thời gian nhất định (trong một khoảng thời gian nhất định) với số điểm ban đầu

D spark Fourier biến đổi

Kết quả của phép biến đổi, chúng ta thu được các giá trị thực và ảo của hàm, được xác định trên dải tần số.

Phép biến đổi Fourier rời rạc nghịch đảo liên kết một hàm tần số, được xác định bởi phổ gấp K trong miền tần số, với một hàm khác, được xác định trong miền thời gian.

N ˗ số giá trị tín hiệu đo được trong mỗi chu kỳ, cũng như tính đa dạng của phổ tần số;

k ˗ chỉ số tần số.

Như đã đề cập, phép biến đổi Fourier rời rạc ánh xạ N điểm của một tín hiệu rời rạc thành N mẫu phổ phức tạp của tín hiệu. Tính toán một mẫu phổ yêu cầu N phép toán của phép nhân và phép cộng phức tạp. Do đó, độ phức tạp tính toán của thuật toán biến đổi Fourier rời rạc là bậc hai, hay nói cách khác, cần phải có các phép toán nhân và cộng phức.

Biến đổi Fourier - một phép biến đổi so sánh các chức năng của một số biến thực. Thao tác này được thực hiện mỗi khi chúng ta cảm nhận các âm thanh khác nhau. Tai thực hiện một "phép tính" tự động, mà ý thức của chúng ta có khả năng thực hiện chỉ sau khi nghiên cứu phần tương ứng của toán học cao hơn. Cơ quan thính giác của con người tạo ra một sự biến đổi, do đó âm thanh (chuyển động dao động của các hạt có điều kiện trong môi trường đàn hồi lan truyền dưới dạng sóng trong môi trường rắn, lỏng hoặc khí) được tạo ra dưới dạng một phổ có giá trị liên tiếp Mức âm lượng của các âm có độ cao khác nhau. Sau đó, não bộ sẽ biến thông tin này thành âm thanh quen thuộc với mọi người.

Biến đổi Fourier toán học

Sự biến đổi của sóng âm hoặc các quá trình dao động khác (từ bức xạ ánh sáng và thủy triều đến các chu kỳ hoạt động của sao hoặc mặt trời) cũng có thể được thực hiện bằng cách sử dụng các phương pháp toán học. Vì vậy, bằng cách sử dụng các kỹ thuật này, có thể phân rã các hàm bằng cách biểu diễn các quá trình dao động dưới dạng một tập hợp các thành phần hình sin, nghĩa là, các đường cong lượn sóng đi từ cực tiểu đến cực đại, rồi lại đến cực tiểu, giống như sóng biển. Biến đổi Fourier - một phép biến đổi có chức năng mô tả pha hoặc biên độ của mỗi hình sin tương ứng với một tần số nhất định. Pha là điểm bắt đầu của đường cong và biên độ là độ cao của nó.

Phép biến đổi Fourier (ví dụ được hiển thị trong ảnh) là một công cụ rất mạnh được sử dụng trong các lĩnh vực khoa học khác nhau. Trong một số trường hợp, nó được sử dụng như một phương tiện để giải các phương trình khá phức tạp mô tả các quá trình động lực học xảy ra dưới ảnh hưởng của năng lượng ánh sáng, nhiệt hoặc điện. Trong các trường hợp khác, nó cho phép bạn xác định các thành phần đều đặn trong các tín hiệu dao động phức tạp, nhờ đó bạn có thể diễn giải chính xác các quan sát thực nghiệm khác nhau trong hóa học, y học và thiên văn học.

Tài liệu tham khảo lịch sử

Người đầu tiên áp dụng phương pháp này là nhà toán học người Pháp Jean Baptiste Fourier. Sự biến đổi, sau này được đặt theo tên của ông, ban đầu được sử dụng để mô tả cơ chế dẫn nhiệt. Fourier đã dành toàn bộ cuộc đời trưởng thành của mình để nghiên cứu các đặc tính của nhiệt. Ông đã đóng góp rất lớn vào lý thuyết toán học xác định nghiệm nguyên của phương trình đại số. Fourier là giáo sư phân tích tại Trường Bách khoa, thư ký của Viện Ai Cập học, phục vụ cho hoàng gia, nơi ông nổi bật trong quá trình xây dựng con đường dẫn đến Turin (dưới sự lãnh đạo của ông, hơn 80 nghìn km vuông đầm lầy sốt rét đã ráo nước). Tuy nhiên, tất cả hoạt động sôi nổi này không ngăn cản nhà khoa học thực hiện phân tích toán học. Năm 1802, ông đã suy ra một phương trình mô tả sự truyền nhiệt trong chất rắn. Năm 1807, nhà khoa học đã phát hiện ra một phương pháp giải phương trình này, được gọi là "phép biến đổi Fourier".

Phân tích độ dẫn nhiệt

Nhà khoa học đã áp dụng một phương pháp toán học để mô tả cơ chế dẫn nhiệt. Một ví dụ thuận tiện, trong đó không có khó khăn trong tính toán, là sự truyền nhiệt năng qua một vòng sắt được nhúng vào một bộ phận trong ngọn lửa. Để thực hiện các thí nghiệm, Fourier đã nung nóng đỏ một phần của chiếc vòng này và chôn nó trong cát mịn. Sau đó, anh ta đo nhiệt độ ở phía đối diện của nó. Ban đầu, sự phân bố nhiệt không đều: một phần của vòng lạnh và phần kia nóng; có thể quan sát thấy một gradient nhiệt độ rõ nét giữa các vùng này. Tuy nhiên, trong quá trình truyền nhiệt trên toàn bộ bề mặt của kim loại, nó trở nên đồng đều hơn. Vì vậy, chẳng bao lâu nữa quá trình này có dạng một hình sin. Lúc đầu, đồ thị tăng dần và cũng giảm một cách trơn tru, chính xác theo quy luật biến thiên của hàm số cosin hay hàm số sin. Sóng giảm dần và kết quả là nhiệt độ trở nên giống nhau trên toàn bộ bề mặt của vòng.

Tác giả của phương pháp này gợi ý rằng phân bố không đều ban đầu có thể được phân tích thành một loạt các hình sin cơ bản. Mỗi người trong số họ sẽ có pha riêng (vị trí ban đầu) và nhiệt độ tối đa của riêng nó. Ngoài ra, mỗi thành phần như vậy thay đổi từ tối thiểu đến tối đa và quay trở lại trên một vòng quay hoàn toàn xung quanh vòng một số nguyên lần. Một thành phần có một chu kỳ được gọi là sóng hài cơ bản và một giá trị có hai hoặc nhiều chu kỳ được gọi là thứ hai, v.v. Vì vậy, hàm toán học mô tả nhiệt độ cực đại, pha hoặc vị trí được gọi là biến đổi Fourier của hàm phân phối. Nhà khoa học đã giảm một thành phần đơn lẻ, khó mô tả về mặt toán học, thành một công cụ dễ sử dụng - chuỗi cosine và sin, cùng đưa ra phân phối ban đầu.

Bản chất của phân tích

Áp dụng phép phân tích này vào sự biến đổi của sự truyền nhiệt qua một vật rắn có dạng hình khuyên, nhà toán học lý luận rằng việc tăng chu kỳ của thành phần hình sin sẽ dẫn đến sự phân rã nhanh chóng của nó. Điều này được nhìn thấy rõ ràng trong các sóng hài cơ bản và thứ hai. Ở chế độ thứ hai, nhiệt độ đạt giá trị cực đại và cực tiểu hai lần trong một lần và ở lần trước, chỉ một lần. Nó chỉ ra rằng khoảng cách được bao phủ bởi nhiệt trong điều hòa thứ hai sẽ bằng một nửa khoảng cách trong điều hòa chính. Ngoài ra, gradient trong cái thứ hai cũng sẽ dốc gấp đôi so với cái đầu tiên. Do đó, vì dòng nhiệt cường độ cao hơn truyền đi một quãng đường ngắn gấp đôi, sóng hài này sẽ phân rã nhanh hơn bốn lần so với cơ bản dưới dạng một hàm của thời gian. Trong tương lai, quá trình này sẽ còn nhanh hơn. Các nhà toán học tin rằng phương pháp này cho phép bạn tính toán quá trình phân bố ban đầu của nhiệt độ theo thời gian.

Thách thức đối với những người cùng thời

Thuật toán biến đổi Fourier đã thách thức nền tảng lý thuyết của toán học vào thời điểm đó. Vào đầu thế kỷ 19, hầu hết các nhà khoa học lỗi lạc, bao gồm Lagrange, Laplace, Poisson, Legendre và Biot, đã không chấp nhận tuyên bố của ông rằng sự phân bố nhiệt độ ban đầu bị phân hủy thành các thành phần ở dạng sóng hài cơ bản và tần số cao hơn. Tuy nhiên, Viện Hàn lâm Khoa học không thể bỏ qua kết quả thu được của nhà toán học và trao giải thưởng cho lý thuyết về các định luật dẫn nhiệt, cũng như so sánh nó với các thí nghiệm vật lý. Trong cách tiếp cận của Fourier, sự phản đối chính là thực tế rằng hàm không liên tục được biểu diễn bằng tổng của một số hàm hình sin liên tục. Rốt cuộc, họ mô tả các đường thẳng và cong bị rách. Những người cùng thời với nhà khoa học chưa bao giờ gặp phải trường hợp tương tự, khi các hàm không liên tục được mô tả bằng sự kết hợp của các hàm liên tục, chẳng hạn như bậc hai, tuyến tính, hình sin hoặc hàm mũ. Trong trường hợp nhà toán học đã đúng trong các phát biểu của mình, thì tổng của một chuỗi vô hạn của một hàm lượng giác sẽ được giảm xuống một chính xác từng bước. Vào thời điểm đó, một tuyên bố như vậy có vẻ vô lý. Tuy nhiên, bất chấp những nghi ngờ, một số nhà nghiên cứu (ví dụ như Claude Navier, Sophie Germain) đã mở rộng phạm vi nghiên cứu và đưa chúng ra ngoài phân tích sự phân bố của năng lượng nhiệt. Trong khi đó, các nhà toán học tiếp tục đau đầu với câu hỏi liệu tổng của một số hàm hình sin có thể được rút gọn thành một biểu diễn chính xác của một hàm không liên tục hay không.

200 năm lịch sử

Lý thuyết này đã phát triển hơn hai thế kỷ, ngày nay nó cuối cùng đã hình thành. Với sự trợ giúp của nó, các chức năng không gian hoặc thời gian được chia thành các thành phần hình sin, có tần số, pha và biên độ riêng. Phép biến đổi này thu được bằng hai phương pháp toán học khác nhau. Hàm đầu tiên trong số chúng được sử dụng khi hàm gốc là liên tục và hàm thứ hai - khi nó được biểu diễn bằng một tập hợp các thay đổi riêng lẻ rời rạc. Nếu biểu thức nhận được từ các giá trị được xác định bởi các khoảng rời rạc, thì nó có thể được chia thành nhiều biểu thức hình sin với các tần số rời rạc - từ thấp nhất rồi cao hơn gấp đôi, ba lần, v.v. Một tổng như vậy được gọi là chuỗi Fourier. Nếu biểu thức ban đầu được cho một giá trị cho mỗi số thực, thì nó có thể được phân tách thành một số tần số hình sin của tất cả các tần số có thể. Nó thường được gọi là tích phân Fourier, và lời giải ngụ ý các phép biến đổi tích phân của hàm. Bất kể cách chuyển đổi thu được như thế nào, hai số phải được chỉ định cho mỗi tần số: biên độ và tần số. Các giá trị này được thể hiện dưới dạng một Lý thuyết đơn về các biểu thức của các biến số phức tạp cùng với phép biến đổi Fourier giúp thực hiện các phép tính trong thiết kế các mạch điện khác nhau, phân tích các dao động cơ học, nghiên cứu cơ chế của truyền sóng và hơn thế nữa.

Biến đổi Fourier ngày nay

Ngày nay, việc nghiên cứu quá trình này chủ yếu chỉ tập trung vào việc tìm ra các phương pháp hiệu quả để chuyển từ một hàm sang dạng biến đổi của nó và ngược lại. Giải pháp này được gọi là phép biến đổi Fourier trực tiếp và nghịch đảo. Nó có nghĩa là gì? Để tạo ra một phép biến đổi Fourier trực tiếp, người ta có thể sử dụng các phương pháp toán học hoặc phương pháp phân tích. Mặc dù thực tế có những khó khăn nhất định khi sử dụng chúng trong thực tế, nhưng hầu hết các tích phân đều đã được tìm thấy và đưa vào sách tham khảo toán học. Với sự trợ giúp của phương pháp số, người ta có thể tính toán các biểu thức có dạng dựa trên dữ liệu thực nghiệm, hoặc các hàm có tích phân không có trong bảng và khó trình bày dưới dạng giải tích.

Trước khi công nghệ máy tính ra đời, việc tính toán các phép biến đổi như vậy rất tẻ nhạt, chúng yêu cầu thực hiện thủ công một số lượng lớn các phép toán số học, phụ thuộc vào số điểm mô tả hàm sóng. Để tạo điều kiện thuận lợi cho việc tính toán, ngày nay có những chương trình đặc biệt cho phép thực hiện những chương trình mới. Vì vậy, vào năm 1965, James Cooley và John Tukey đã tạo ra phần mềm được gọi là "Fast Fourier Transform". Nó cho phép bạn tiết kiệm thời gian tính toán bằng cách giảm số lượng phép nhân trong phân tích đường cong. Phương pháp biến đổi Fourier nhanh dựa trên việc chia đường cong thành một số lượng lớn các giá trị mẫu đồng nhất. Theo đó, số phép nhân giảm đi một nửa cùng với số điểm giảm đi.

Áp dụng Biến đổi Fourier

Quá trình này được sử dụng trong các lĩnh vực khoa học khác nhau: trong vật lý, xử lý tín hiệu, tổ hợp, lý thuyết xác suất, mật mã, thống kê, đại dương học, quang học, âm học, hình học và các lĩnh vực khác. Khả năng ứng dụng phong phú của nó dựa trên một số tính năng hữu ích, được gọi là "thuộc tính biến đổi Fourier". Hãy xem xét chúng.

1. Phép biến đổi của một hàm là một toán tử tuyến tính và, với sự chuẩn hóa thích hợp, là đơn nhất. Tính chất này được gọi là định lý Parseval, hay nói chung là định lý Plancherel, hay thuyết nhị nguyên của Pontryagin.

2. Phép biến hình là thuận nghịch. Hơn nữa, kết quả nghịch đảo có dạng gần giống như trong phương pháp giải trực tiếp.

3. Biểu thức cơ sở hình sin là hàm phân biệt riêng. Điều này có nghĩa là một biểu diễn như vậy sẽ thay đổi với một hệ số không đổi thành những biểu diễn đại số thông thường.

4. Theo định lý "tích chập", quá trình này biến một phép toán phức tạp thành một phép nhân sơ cấp.

5. Phép biến đổi Fourier rời rạc có thể được tính nhanh trên máy tính bằng phương pháp "nhanh".

Các loại biến đổi Fourier

1. Thông thường, thuật ngữ này được sử dụng để biểu thị một phép biến đổi liên tục cung cấp bất kỳ biểu thức tích phân bình phương nào dưới dạng tổng của các biểu thức hàm mũ phức với các tần số và biên độ góc cụ thể. Loại này có một số dạng khác nhau, có thể khác nhau về hệ số không đổi. Phương pháp liên tục bao gồm một bảng chuyển đổi, có thể được tìm thấy trong các sách tham khảo toán học. Một trường hợp tổng quát là một phép biến đổi phân số, bằng cách đó quá trình đã cho có thể được nâng lên thành công suất thực cần thiết.

2. Phương pháp liên tục là tổng quát của kỹ thuật sơ khai của chuỗi Fourier, được định nghĩa cho các hàm hoặc biểu thức tuần hoàn khác nhau tồn tại trong một vùng giới hạn và biểu diễn chúng dưới dạng một chuỗi hình sin.

3. Biến đổi Fourier rời rạc. Phương pháp này được sử dụng trong công nghệ máy tính để tính toán khoa học và xử lý tín hiệu số. Để thực hiện kiểu tính toán này, cần phải có các hàm xác định các điểm riêng lẻ, các vùng tuần hoàn hoặc giới hạn trên một tập rời rạc thay vì các tích phân Fourier liên tục. Sự biến đổi tín hiệu trong trường hợp này được biểu diễn dưới dạng tổng của các hình sin. Đồng thời, việc sử dụng phương pháp "nhanh" cho phép sử dụng các giải pháp rời rạc cho bất kỳ vấn đề thực tế nào.

4. Phép biến đổi Fourier có cửa sổ là một dạng tổng quát của phương pháp cổ điển. Ngược lại với giải pháp tiêu chuẩn, khi được sử dụng, giải pháp này được thực hiện trên toàn bộ phạm vi tồn tại của một biến nhất định, ở đây chỉ phân bố tần số cục bộ được quan tâm đặc biệt, với điều kiện là biến ban đầu (thời gian) được bảo toàn.

5. Phép biến đổi Fourier hai chiều. Phương pháp này được sử dụng để làm việc với mảng dữ liệu hai chiều. Trong trường hợp này, phép biến đổi được thực hiện trước tiên theo một hướng, sau đó theo hướng khác.

Sự kết luận

Ngày nay, phương pháp Fourier đã được sử dụng vững chắc trong các lĩnh vực khoa học khác nhau. Ví dụ, vào năm 1962, hình dạng của chuỗi xoắn kép DNA được phát hiện bằng cách sử dụng phân tích Fourier kết hợp với phương pháp sau tập trung vào các tinh thể của sợi DNA, kết quả là hình ảnh thu được do nhiễu xạ bức xạ đã được ghi lại trên phim. Hình ảnh này cung cấp thông tin về giá trị của biên độ khi sử dụng phép biến đổi Fourier cho một cấu trúc tinh thể nhất định. Dữ liệu pha thu được bằng cách so sánh bản đồ nhiễu xạ DNA với bản đồ thu được từ việc phân tích các cấu trúc hóa học tương tự. Kết quả là các nhà sinh vật học đã khôi phục lại cấu trúc tinh thể - chức năng ban đầu.

Các phép biến đổi Fourier đóng một vai trò to lớn trong việc nghiên cứu không gian bên ngoài, vật lý bán dẫn và plasma, âm học vi sóng, hải dương học, radar, địa chấn học và khám sức khỏe.

Các phép biến đổi này là hàm vì chúng biến một số hàm của một biến thành một hàm hoàn toàn khác của một biến và ngược lại.

Các phép biến đổi Fourier có dạng:

Phương trình tích phân (4.34) được gọi là phương trình trực tiếp, và phương trình (4.35) được gọi là biến đổi Fourier ngược. Viết tắt cho các phương trình này

Tích phân Fourier (biến đổi Fourier trực tiếp) cho phép bạn mở rộng một hàm không tuần hoàn có tính chất tích phân tuyệt đối trong các giới hạn nhất định thành một chuỗi vô hạn các sóng hài tạo thành một phổ tần số liên tục trong phạm vi từ đến với tần số nhỏ vô hạn. khoảng thời gian giữa các sóng hài liền kề (tức là trong giới hạn

Phương pháp biến đổi Fourier không phù hợp với các điều kiện ban đầu (hoặc biên) khác không. Phương pháp này chỉ có thể được áp dụng khi các hàm mong muốn có ảnh Fourier, tức là đối với các hàm thời gian hoàn toàn có thể tích hợp thỏa mãn bất đẳng thức

Các hàm phổ biến nhất trong lý thuyết điều khiển là hàm bước đơn vị (1.44) và tích của hàm hình sin và hàm đơn vị (1.51). Biến đổi Fourier không áp dụng cho bất kỳ hàm nào trong số này, vì điều kiện (4.38) không được thỏa mãn.

Những thiếu sót này hạn chế việc sử dụng phương pháp biến đổi Fourier.

Để áp dụng tích phân Fourier, cần phải chọn một hàm đủ gần với hàm đang nghiên cứu, ví dụ, với một hàm bậc ở các giá trị hữu hạn, nhưng đồng thời thỏa mãn điều kiện (4.38). Chức năng này có thể nhận được bằng cách nhân

hàm bước trên đó c là một giá trị dương đủ nhỏ. Chức năng trợ giúp mới có được

Đặt c có xu hướng bằng 0 và chuyển đến giới hạn, chúng ta có thể chuyển từ hàm phụ sang hàm chính. Ngoài ra, nếu chúng ta tự giới hạn bản thân ở các hàm giống hệt 0 thì điều kiện (4.38) sẽ giữ cho một lớp lớn của các hàm và chúng ta có thể tìm thấy phổ tần số của hàm bằng cách sử dụng biểu thức (4.34). Thay vào đó, chúng tôi giới thiệu một ký hiệu mới, vì số lượng này bây giờ cũng phụ thuộc vào c:

Đưa với tìm

Công thức này trùng với phép biến đổi Laplace trực tiếp (4.9).

Theo đó, phép biến đổi Fourier có thể được coi là một trường hợp đặc biệt của phép biến đổi Laplace.

Các phương pháp biến đổi được mô tả ở trên cho phép chúng tôi rút ra các kết luận sau:

1) phương trình vi phân-tích phân được thay thế bằng phương trình đại số;

2) hoạt động xác định các hằng số tích hợp bị loại bỏ, vì các điều kiện ban đầu được tính đến ngay từ đầu khi tìm hình ảnh của giá trị mong muốn;

3) hoạt động xác định gốc của phương trình đặc trưng được bảo toàn hoàn toàn.

Thuận tiện nhất cho việc giải các bài toán thực tế là phương pháp biến đổi Laplace. Ở dạng sửa đổi một chút, nó có thể được áp dụng để nghiên cứu ACS rời rạc (xem Chương 7).

Xem xét việc sử dụng phương pháp biến đổi Laplace để giải một phương trình vi phân có dạng

Chúng tôi biến đổi phương trình vi phân này bằng cách sử dụng phép biến đổi Laplace trực tiếp (4.9) và các Định lý 1 và 2. Kết quả là, chúng tôi thu được một phương trình đại số được viết cho hình ảnh:

trong đó là tổng của tất cả các số hạng có chứa các điều kiện ban đầu.

Từ đây là hình ảnh của chức năng mong muốn

Đối với các điều kiện ban đầu bằng không, các biểu thức (4.41) và (4.42) được đơn giản hóa:

Khi biết hình ảnh của chức năng mong muốn, bạn có thể tìm bản gốc, ví dụ, từ các bảng hình ảnh.

Nếu hình ảnh của giá trị mong muốn là một phân số hữu tỉ, thì họ cố gắng viết nó dưới dạng tổng của các phân số đơn giản với hệ số không đổi. Phép biến đổi ngược cho mỗi phân số đơn giản này có thể nhận được từ các bảng và biểu thức cuối cùng của gốc được trình bày dưới dạng tổng các giá trị riêng lẻ được tìm thấy. Bạn cũng có thể sử dụng định lý phân rã để xác định gốc.

Nếu ảnh Laplace là một phân số hữu tỉ có dạng

Xem xét các tính chất cơ bản của phép biến đổi Fourier.

Tuyến tính. Xem xét các chức năng và với quang phổ và :

(12)

Khi đó phổ của sự kết hợp tuyến tính của chúng sẽ là:

Thời gian trễ. Chúng tôi giả định rằng phổ đã biết dấu hiệu

(14)

Hãy tính phổ của tín hiệu dịch chuyển theo thời gian: . Biểu thị đối số hàm của biến mới , sau đó và

Tín hiệu bị trễ một lúc dẫn đến việc nhân rộng phổ bằng .

Thay đổi quy mô. Chúng tôi giả định rằng phổ đã biết dấu hiệu như thông qua phổ tín hiệu được thể hiện . Chúng tôi giới thiệu một biến mới , chúng tôi thay đổi biến tích hợp .

(16)

Nhân với 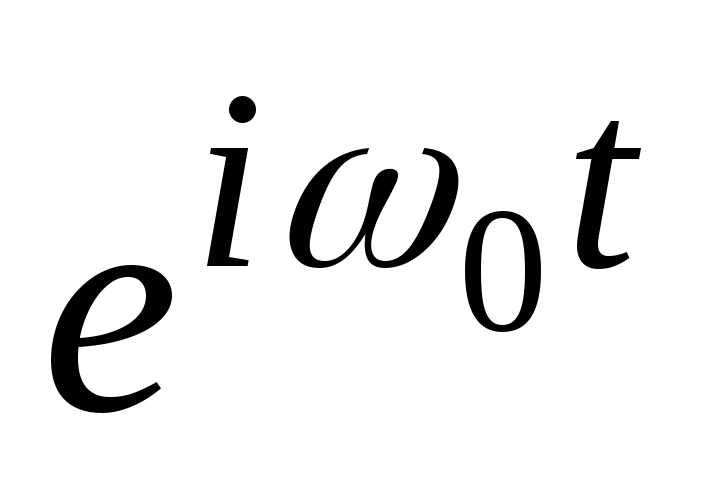. Như trong trường hợp trước, chúng tôi giả định rằng phổ đã biết dấu hiệu . Tìm phổ của tín hiệu này, nhân với .

Do đó, nhân tín hiệu với dẫn đến sự thay đổi của quang phổ bằng cách .

Phổ đạo hàm. Trong trường hợp này, điểm mấu chốt là tính tích hợp tuyệt đối của hàm. Từ thực tế là tích phân của môđun của một hàm phải có giới hạn, điều đó dẫn đến rằng ở vô cùng hàm phải có xu hướng bằng không. Tích phân của đạo hàm của hàm được lấy theo từng phần, các số hạng không tích phân thu được bằng 0, vì hàm có xu hướng bằng 0 ở vô cùng.

(18)

Phổ của tích phân. Hãy tìm phổ của tín hiệu . Và chúng tôi sẽ giả định rằng , nghĩa là, tín hiệu không có thành phần bất biến. Yêu cầu này là cần thiết để các số hạng bên ngoài tích phân bằng 0 khi tích phân được lấy theo từng phần.

(19)

Định lý tích lũy.Được biết rằng và quang phổ chức năng và tương ứng. Nó được yêu cầu để thể hiện phổ tích chập bởi vì và . Để làm điều này, trong tích phân Fourier của tích chập, một trong các hàm sẽ được thay thế bằng biến , thì số mũ có thể được thay thế . Kết quả của sự thay thế như vậy, tích phân kép sẽ bằng tích của hai tích phân Fourier.

(20)

Biến đổi Fourier của tích chập của hai tín hiệu cho ra tích của phổ của các tín hiệu này.

Sản xuất tín hiệu.Được biết rằng và là phổ của các chức năng và tương ứng. Nó được yêu cầu để thể hiện phổ của sản phẩm thông qua quang phổ và . Ví dụ, chúng ta hãy thay thế thành tích phân Fourier thay vì một trong các tín hiệu , biểu thức của nó dưới dạng biến đổi Fourier ngược, và sau đó thay đổi thứ tự tích phân.

(21)

Phổ của sản phẩm của các tín hiệu là tích chập của phổ của các tín hiệu này.

Phổ tín hiệu rời rạc

Cần đặc biệt chú ý đến các tín hiệu rời rạc, vì các tín hiệu này được sử dụng trong xử lý kỹ thuật số. Tín hiệu rời rạc, không giống như tín hiệu liên tục, là một dãy số tương ứng với các giá trị của tín hiệu liên tục tại một số thời điểm nhất định. Một tín hiệu rời rạc có điều kiện có thể được coi là một tín hiệu liên tục, tại những thời điểm nhất định nhận một số giá trị và tại những thời điểm khác thì bằng không. Vì vậy, ví dụ, rời rạc tín hiệu có thể được đưa ra như là sản phẩm của một tín hiệu liên tục trên một chuỗi các xung hình chữ nhật lặp lại định kỳ - xung thời gian (Hình 1).

Cơm. 1. Tùy biến tín hiệu.

(22)

Xung hình chữ nhật có thời lượng , khoảng thời gian lặp lại :

(23)

Biên độ xung được chọn sao cho tích phân của xung trong khoảng thời gian bằng . Trong trường hợp này, xung đồng hồ là không có thứ nguyên. Chúng tôi mở rộng chuỗi các xung động như vậy thành một chuỗi lượng giác:

(24)

Để có được kết quả đọc tín hiệu tức thì , cần phải hướng thời lượng xung về 0: . Chúng tôi gọi một tín hiệu đồng hồ như vậy là lý tưởng. Trong trường hợp này, hệ số mở rộng trong chuỗi Fourier tất cả sẽ bằng 1.

(25)

Chính xác cùng một dạng có khai triển trong chuỗi Fourier của hàm:

(26)

Hệ số khai triển thành một chuỗi lượng giác của tín hiệu đồng hồ :

(27)

Khi đó, tín hiệu rời rạc sẽ giống như sau:

Khi tính toán biến đổi Fourier của một tín hiệu rời rạc, chúng tôi hoán đổi hoạt động của tổng và tích hợp, sau đó sử dụng thuộc tính δ - Chức năng:

Phổ của một tín hiệu rời rạc là một hàm tuần hoàn. Xem xét số mũ trong thuật ngữ khách sạn như một hàm của tần số. Khoảng thời gian lặp lại của nó là . Khoảng thời gian lặp lại dài nhất cho các thuật ngữ có số , và theo đó, đây sẽ là khoảng thời gian lặp lại của toàn bộ quang phổ. I E phổ của tín hiệu rời rạc có chu kỳ lặp lại bằng tần số lượng tử hóa .

Hãy xem một chương trình khác . Do thực tế rằng là một sản phẩm của các chức năng và , phổ của tín hiệu rời rạc được tính dưới dạng tích chập của phổ của tín hiệu liên tục và phổ của tín hiệu đồng hồ .

(30)

Tính toán đang sử dụng (25). Như chức năng tuần hoàn, phổ của nó là rời rạc.

So chập (30)

Theo biểu thức (32), phổ của tín hiệu rời rạc là một hàm lặp lại định kỳ .

Thực tế là những thay đổi về chất xảy ra trong phổ tín hiệu do kết quả của việc lấy mẫu cho thấy rằng tín hiệu ban đầu có thể bị bóp méo, vì nó hoàn toàn được xác định bởi phổ của nó. Tuy nhiên, mặt khác, sự lặp lại tuần hoàn của cùng một phổ tự bản thân nó không tạo ra bất cứ điều gì mới vào phổ, do đó, trong những điều kiện nhất định, biết các giá trị tín hiệu tại một số thời điểm nhất định, bạn có thể tìm thấy giá trị của tín hiệu này. lấy tại bất kỳ thời điểm nào khác, tức là nhận được tín hiệu liên tục ban đầu. Đây là ý nghĩa của định lý Kotelnikov, định lý này đặt ra một điều kiện về sự lựa chọn tần số lượng tử hóa phù hợp với tần số cực đại trong phổ tín hiệu.

Nếu điều kiện này bị vi phạm, thì sau khi số hóa tín hiệu, một phổ lặp lại định kỳ sẽ được chồng lên (Hình 2). Phổ thu được từ lớp phủ sẽ tương ứng với một tín hiệu khác.

Cơm. 2. Sự xen phủ quang phổ.

Loạt bài này cũng có thể được viết thành:

(2),trong đó, biên độ phức thứ k.

Mối quan hệ giữa các hệ số (1) và (3) được biểu thị bằng các công thức sau:

Lưu ý rằng tất cả ba biểu diễn này của chuỗi Fourier là hoàn toàn tương đương. Đôi khi, khi làm việc với chuỗi Fourier, sẽ thuận tiện hơn khi sử dụng số mũ của đối số ảo thay vì sin và cosin, tức là sử dụng phép biến đổi Fourier ở dạng phức. Nhưng thuận tiện cho chúng ta là sử dụng công thức (1), trong đó chuỗi Fourier được biểu diễn dưới dạng tổng các sóng cosin với các biên độ và pha tương ứng. Trong mọi trường hợp, sẽ không chính xác khi nói rằng kết quả của phép biến đổi Fourier của tín hiệu thực sẽ là các biên độ phức tạp của sóng hài. Như wiki đã nói một cách chính xác, "Phép biến đổi Fourier (?) Là một phép toán ánh xạ một hàm của một biến thực sang một hàm khác, cũng của một biến thực."

Toàn bộ:Cơ sở toán học của phép phân tích quang phổ của tín hiệu là phép biến đổi Fourier.

Phép biến đổi Fourier cho phép chúng ta biểu diễn một hàm liên tục f (x) (tín hiệu) được xác định trên đoạn (0, T) dưới dạng tổng của một số vô hạn (chuỗi vô hạn) của các hàm lượng giác (sin và / hoặc cosin) với các biên độ nhất định và các pha, cũng được xem xét trên phân đoạn (0, T). Chuỗi như vậy được gọi là chuỗi Fourier.

Chúng tôi lưu ý thêm một số điểm, cần phải hiểu rõ về điểm này để áp dụng đúng phép biến đổi Fourier vào phân tích tín hiệu. Nếu chúng ta xem xét chuỗi Fourier (tổng các hình sin) trên toàn bộ trục X, thì chúng ta có thể thấy rằng bên ngoài đoạn (0, T), hàm được biểu diễn bởi chuỗi Fourier sẽ lặp lại định kỳ hàm của chúng ta.

Ví dụ, trong đồ thị ở Hình 7, hàm gốc được xác định trên đoạn (-T \ 2, + T \ 2) và chuỗi Fourier biểu thị một hàm tuần hoàn được xác định trên toàn bộ trục x.

Điều này là do bản thân các hình sin tương ứng là các hàm tuần hoàn và tổng của chúng sẽ là một hàm tuần hoàn.

Hình 7 Biểu diễn một hàm gốc không tuần hoàn bằng chuỗi Fourier

Như vậy:

Nguyên hàm của chúng ta là liên tục, không tuần hoàn, được xác định trên một khoảng độ dài T nào đó. Phổ của hàm này là rời rạc, nghĩa là, nó được trình bày dưới dạng một chuỗi vô hạn của các thành phần hài - chuỗi Fourier. Trên thực tế, một hàm tuần hoàn nhất định được xác định bởi chuỗi Fourier, nó trùng với của chúng ta trên đoạn (0, T), nhưng tính tuần hoàn này không cần thiết đối với chúng ta.

Chu kỳ của các thành phần điều hòa là bội số của đoạn (0, T) mà trên đó nguyên hàm f (x) được xác định. Nói cách khác, chu kỳ sóng hài là bội số của khoảng thời gian đo tín hiệu. Ví dụ, chu kỳ của điều hòa đầu tiên của chuỗi Fourier bằng khoảng thời gian T mà trên đó hàm f (x) được xác định. Chu kỳ của dao động điều hòa thứ hai trong chuỗi Fourier bằng khoảng T / 2. Và như vậy (xem Hình 8).

Hình 8 Các chu kỳ (tần số) của các thành phần hài của chuỗi Fourier (ở đây T = 2?)

Theo đó, tần số của các thành phần sóng hài là bội số của 1 / T. Tức là, tần số của các thành phần hài Fk bằng Fk = k \ T, trong đó k nằm trong khoảng từ 0 đến?, Ví dụ, k = 0 F0 = 0; k = 1 F1 = 1 \ T; k = 2 F2 = 2 \ T; k = 3 F3 = 3 \ T;… Fk = k \ T (ở tần số 0 - thành phần không đổi).

Giả sử hàm ban đầu của chúng ta là một tín hiệu được ghi lại trong T = 1 giây. Khi đó chu kỳ của sóng hài thứ nhất sẽ bằng khoảng thời gian của tín hiệu T1 = T = 1 giây và tần số của sóng hài là 1 Hz. Chu kỳ của sóng hài thứ hai sẽ bằng khoảng thời gian của tín hiệu chia cho 2 (T2 = T / 2 = 0,5 giây) và tần số là 2 Hz. Cho dao động thứ ba T3 = T / 3 giây và tần số là 3 Hz. Vân vân.

Bước giữa các sóng hài trong trường hợp này là 1 Hz.

Do đó, tín hiệu có thời lượng 1 giây có thể bị phân hủy thành các thành phần sóng hài (để thu được phổ) với độ phân giải tần số 1 Hz. Để tăng độ phân giải lên 2 lần đến 0,5 Hz, cần tăng thời lượng đo lên 2 lần - tối đa 2 giây. Một tín hiệu có thời gian 10 giây có thể bị phân hủy thành các thành phần hài (để thu được phổ) với độ phân giải tần số 0,1 Hz. Không có cách nào khác để tăng độ phân giải tần số.

Có một cách để tăng thời lượng của tín hiệu một cách giả tạo bằng cách thêm các số không vào mảng mẫu. Nhưng nó không làm tăng độ phân giải tần số thực.

3. Tín hiệu rời rạc và biến đổi Fourier rời rạc

Với sự phát triển của công nghệ kỹ thuật số, các cách thức lưu trữ dữ liệu đo lường (tín hiệu) cũng đã thay đổi. Nếu trước đây, tín hiệu có thể được ghi trên máy ghi âm và lưu trên băng ở dạng tương tự thì giờ đây, tín hiệu đã được số hóa và lưu trữ trong các tệp trong bộ nhớ của máy tính dưới dạng một tập hợp các số (số đếm).

Sơ đồ thông thường để đo và số hóa tín hiệu như sau.

Hình 9 Sơ đồ kênh đo

Tín hiệu từ đầu dò đo đến ADC trong khoảng thời gian T. Các mẫu tín hiệu (mẫu) thu được trong thời gian T được chuyển đến máy tính và lưu trong bộ nhớ.

Hình 10 Tín hiệu số hóa - N lần đọc nhận được trong thời gian T

Các yêu cầu đối với thông số số hóa tín hiệu là gì? Một thiết bị chuyển đổi tín hiệu tương tự đầu vào thành mã rời (tín hiệu kỹ thuật số) được gọi là bộ chuyển đổi tín hiệu tương tự sang số (ADC, tiếng Anh Analog-to-digital converter, ADC) (Wiki).

Một trong những tham số chính của ADC là tốc độ lấy mẫu tối đa (hay tốc độ lấy mẫu, tiếng Anh là tốc độ lấy mẫu) - tần suất lấy mẫu của một tín hiệu liên tục theo thời gian trong quá trình lấy mẫu của nó. Được đo bằng hertz. ((Wiki))

Theo định lý Kotelnikov, nếu một tín hiệu liên tục có phổ giới hạn bởi tần số Fmax, thì nó có thể được khôi phục hoàn toàn và duy nhất từ ​​các mẫu rời rạc của nó được lấy trong các khoảng thời gian. , I E. với tần số Fd? 2 * Fmax, trong đó Fd - tốc độ lấy mẫu; Fmax - tần số cực đại của phổ tín hiệu. Nói cách khác, tốc độ lấy mẫu tín hiệu (tốc độ lấy mẫu ADC) ít nhất phải gấp 2 lần tần số tối đa của tín hiệu mà chúng ta muốn đo.

Và điều gì sẽ xảy ra nếu chúng ta đọc các bài đọc với tần số thấp hơn yêu cầu của định lý Kotelnikov?

Trong trường hợp này, xảy ra hiệu ứng "răng cưa" (hay còn gọi là hiệu ứng đèn pha, hiệu ứng moiré), trong đó tín hiệu tần số cao sau khi số hóa chuyển thành tín hiệu tần số thấp không thực sự tồn tại. Trên hình. 5 tần số cao sóng hình sin màu đỏ là tín hiệu thực. Sóng hình sin tần số thấp hơn màu xanh lam là tín hiệu giả do hơn nửa chu kỳ của tín hiệu tần số cao có thời gian trôi qua trong thời gian lấy mẫu.

Cơm. 11. Sự xuất hiện của tín hiệu tần số thấp sai khi tốc độ lấy mẫu không đủ cao

Để tránh ảnh hưởng của hiện tượng răng cưa, một bộ lọc khử răng cưa đặc biệt được đặt trước ADC - LPF (bộ lọc thông thấp), bộ lọc này cho tần số thấp hơn một nửa tần số lấy mẫu ADC và cắt các tần số cao hơn.

Để tính toán phổ của tín hiệu từ các mẫu rời rạc của nó, phép biến đổi Fourier rời rạc (DFT) được sử dụng. Chúng tôi lưu ý một lần nữa rằng phổ của tín hiệu rời rạc "theo định nghĩa" bị giới hạn bởi tần số Fmax, nhỏ hơn một nửa tần số lấy mẫu Fd. Do đó, phổ của tín hiệu rời rạc có thể được biểu diễn bằng tổng của một số lượng hài hữu hạn, ngược lại với tổng vô hạn đối với chuỗi Fourier của tín hiệu liên tục, phổ của chúng có thể là không giới hạn. Theo định lý Kotelnikov, tần số sóng hài lớn nhất phải sao cho nó chiếm ít nhất hai mẫu, do đó số lượng hài bằng một nửa số mẫu của tín hiệu rời rạc. Tức là nếu có N mẫu trong mẫu thì số lượng hài trong phổ sẽ bằng N / 2.

Bây giờ hãy xem xét phép biến đổi Fourier rời rạc (DFT).

So sánh với chuỗi Fourier

Chúng ta thấy rằng chúng trùng hợp, ngoại trừ thời gian trong DFT là rời rạc và số lượng hài được giới hạn ở N / 2 - một nửa số mẫu.

Công thức DFT được viết bằng các biến số nguyên không thứ nguyên k, s, trong đó k là số lượng mẫu tín hiệu, s là số lượng các thành phần phổ. Giá trị của s biểu thị số lần dao động điều hòa trong khoảng thời gian T (khoảng thời gian đo tín hiệu). Phép biến đổi Fourier rời rạc được sử dụng để tìm biên độ và pha của sóng hài bằng số, tức là "trên máy tính"

Quay lại kết quả thu được lúc đầu. Như đã đề cập ở trên, khi mở rộng một hàm không tuần hoàn (tín hiệu của chúng ta) thành một chuỗi Fourier, chuỗi Fourier thu được thực sự tương ứng với một hàm tuần hoàn với chu kỳ T. (Hình 12).

Hình 12 Hàm tuần hoàn f (x) với chu kỳ Т0, với chu kỳ đo Т> T0

Như có thể thấy trong Hình 12, hàm f (x) là tuần hoàn với chu kỳ Т0. Tuy nhiên, do khoảng thời gian của mẫu đo T không trùng với chu kỳ của hàm T0, hàm thu được dưới dạng chuỗi Fourier có sự gián đoạn tại điểm T. Do đó, phổ của hàm này sẽ chứa một số lượng lớn các sóng hài tần số cao. Nếu khoảng thời gian của mẫu đo T trùng với chu kỳ của hàm T0, thì chỉ có hài bậc nhất (hình sin có chu kỳ bằng thời gian của mẫu) mới có mặt trong phổ thu được sau phép biến đổi Fourier, vì hàm f (x) là một hình sin.

Nói cách khác, chương trình DFT "không biết" rằng tín hiệu của chúng ta là "một phần của sóng sin", nhưng đang cố gắng biểu diễn một hàm tuần hoàn dưới dạng một chuỗi, có khoảng cách do sự không nhất quán của các phần riêng lẻ của sóng sin.

Kết quả là, các sóng hài xuất hiện trong phổ, về tổng thể, các sóng hài phải đại diện cho dạng của hàm, bao gồm cả sự gián đoạn này.

Vì vậy, để thu được phổ "đúng" của tín hiệu, là tổng của một số hình sin với các chu kỳ khác nhau, cần một số nguyên chu kỳ của mỗi hình sin phù hợp với chu kỳ đo tín hiệu. Trong thực tế, điều kiện này có thể được đáp ứng trong một khoảng thời gian đủ dài của phép đo tín hiệu.

Hình 13 Một ví dụ về chức năng và phổ của tín hiệu lỗi động học của hộp số

Với thời lượng ngắn hơn, bức ảnh sẽ trông "xấu" hơn:

Hình 14 Một ví dụ về chức năng và phổ của tín hiệu rung rôto

Trong thực tế, có thể khó hiểu đâu là "thành phần thực" và đâu là "hiện vật" gây ra bởi sự không đa dạng của các khoảng thời gian của các thành phần và khoảng thời gian của mẫu tín hiệu hoặc "nhảy và ngắt" của dạng sóng. Tất nhiên, các từ "thành phần thực" và "hiện vật" không được trích dẫn một cách vô ích. Sự hiện diện của nhiều sóng hài trên đồ thị phổ không có nghĩa là tín hiệu của chúng ta thực sự “bao gồm” chúng. Nó giống như nghĩ rằng số 7 "bao gồm" các số 3 và 4. Số 7 có thể được biểu diễn dưới dạng tổng của các số 3 và 4 - điều này chính xác.

Tín hiệu của chúng ta cũng vậy ... hay đúng hơn, thậm chí không phải là "tín hiệu của chúng ta", mà là một hàm tuần hoàn được tổng hợp bằng cách lặp lại tín hiệu của chúng ta (lấy mẫu) có thể được biểu diễn dưới dạng tổng của các sóng hài (hình sin) với các biên độ và pha nhất định. Nhưng trong nhiều trường hợp quan trọng đối với thực tế (xem các hình trên), thực sự có thể liên hệ các sóng hài thu được trong phổ với các quá trình thực có bản chất tuần hoàn và đóng góp đáng kể vào hình dạng tín hiệu.

Một số kết quả

1. Tín hiệu thực đo được, thời lượng T giây, được số hóa bởi ADC, được biểu thị bằng một tập mẫu rời rạc (N mảnh), có phổ rời rạc không tuần hoàn, được biểu diễn bằng một tập hài (N / 2 mảnh) ).

2. Tín hiệu được biểu diễn bằng một tập các giá trị thực và phổ của nó được biểu diễn bằng một tập các giá trị thực. Các tần số điều hòa có giá trị dương. Thực tế là thuận tiện hơn cho các nhà toán học khi biểu diễn phổ ở dạng phức hợp bằng cách sử dụng tần số âm không có nghĩa là “nó đúng” và “nó luôn phải được thực hiện theo cách này”.

3. Tín hiệu được đo trên khoảng thời gian T chỉ được xác định trên khoảng thời gian T. Điều gì đã xảy ra trước khi chúng ta bắt đầu đo tín hiệu, và điều gì sẽ xảy ra sau đó - điều này khoa học chưa biết. Và trong trường hợp của chúng tôi - nó không thú vị. DFT của một tín hiệu giới hạn thời gian cho phổ "thực" của nó, theo nghĩa là, trong những điều kiện nhất định, nó cho phép bạn tính toán biên độ và tần số của các thành phần của nó.

Vật liệu đã qua sử dụng và các vật liệu hữu ích khác.