Phương Trình đường Tròn Lớp 10 Chuẩn Nhất - CungHocVui
Có thể bạn quan tâm
Ở trong bài viết này Cunghocvui sẽ gửi đến các bạn những kiến thức lý thuyết về phương trình đường tròn lớp 10, các dạng phương trình đường tròn lớp 10,... Cùng mau đi vào tìm hiểu ngay nhé!
I. Lý thuyết
1. Phương trình đường tròn
- Phương trình đường tròn có tâm I (a;b), bán kính R là \((x-2)^2+(y-b)^2 = R^2\)
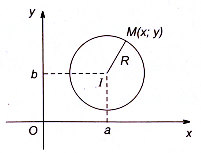
- Phương trình \(x^2 + y^2 - 2ax - 2by + c = 0\) (\(a^2+b^2-c > 0\)) là phương trình của đường tròn tâm I (a;b) và bán kính \(R = \sqrt{a^2+b^2-c}\)
2. Phương trình tiếp tuyến của đường tròn
Cho trước điểm \(M_0(x_0;y_0)\) nằm trên đường tròn (C) tâm I có tọa độ (a;b), tiếp tuyến tại \(M_0\) của (C) có phương trình: \((x_0-a)(x-x_0)+(y_0-b)(y-y_0)=0\)
II. Các dạng bài tập chuyên đề phương trình đường tròn lớp 10
1. Dạng 1: Nhận dạng phương trình đường tròn và tìm điều kiện để một phương trình là phương trình đường tròn
=> Phương pháp giải:
- Cách 1: Đưa phương trình đề bài đã cho về dạng \((x-a)^2+(y-b)^2 = P\) (1)
- Nếu P>0 thì (1) phương trình đường tròn tâm I (a;b) và bán kính R = \(\sqrt{P}\)
- Nếu P\(\leq \)0 thì (1) không phải phải phương trình đường tròn
- Cách 2: Đưa phương trình đề bài đã cho về dạng \(x^2 + y^2 - 2ax - 2by + c = 0\) (2); Đặc P = \(a^2 + b^2 - c\)
- Nếu P > 0 thì (2) là phương trình đường tròn tâm I (a; b) và bán kính R = \(\sqrt{a^2+b^2-c}\)
- Nếu P\(\leq \)0 thì (2) không phải phải phương trình đường tròn
=> Ví dụ: Cho hai phương trình sau:
- \(x^2 + y^2 - 2x - 4y + 9 = 0\)
- \(x^2 + y^2 - 6x + 4y + 13 = 0\)
Hãy cho biết đâu là phương trình đường tròn, tìm tâm và bán kính nếu có.
=> Lời giải:
- \(x^2 + y^2 - 2x - 4y + 9 = 0\)
- Dữ liệu đề bài đã cho, có a = -1; b = 2; c = 9 nên \(a^2 + b^2 - c = (-1)^2+ (2)^2 - 9 = -4 <0\)
- Vậy phương trình đã cho không phải là phương trình đường tròn
- \(x^2 + y^2 - 6x + 4y + 13 = 0\)
- Có: \(a^2 + b^2 - c = 3^2 + (-2)^2-13<0\)
- Vậy phương trình đã cho không phải là phương trình đường tròn
2. Dạng 2: Lập phương trình đường tròn đi qua các điểm
=> Phương pháp:
- Cách 1:
- Tìm tọa độ của tâm I (a;b) thuộc đường tròn (C)
- Tìm ra bán kính R của đường tròn (C) bằng bao nhiêu
- Viết phương trình đường tròn (C) có dạng: \((x-a)^2+(y-b)^2 = R^2\)
- Cách 2: Giả sử \(x^2 + y^2 - 2ax - 2by + c = 0\) là dạng tổng quát của phương trình đường tròn (C)
- Từ điều kiện bài toán cho thiết lập hệ phương trình gồm ba ẩn a, b, c
- Giải hệ ba ẩn a, b, c, thay vào phương trình đường tròn (C)
* Lưu ý: Cho hai điểm A và B, đường tròn (C) đi qua hai điểm này thì \(IA^2 = IB^2 = R^2\). Trường hợp này sẽ thường được vận dụng vào bài toán yêu cầu viết phương trình đường tròn ngoại tiếp tam giác ABC (hay chính là viết phương trình đường tròn khi đi qua ba điểm A, B, C)
=> Ví dụ: Hãy lập phương trình đường tròn (C) khi có tâm I(1;-3) và đi qua điểm O(0;0)
=> Lời giải:
- Có: Đường tròn (C) có tâm I là (1;-3) và đi qua gốc tọa độ O(0;0). Vì vậy R = OI mà \(\left | \underset{OI}{\rightarrow} \right |=\sqrt{1^2+(-3)^2}=\sqrt{10}\)
- Vậy phương trình đường tròn (C) là: \((x-1)^2+ (y+3)^2=10\)
3. Dạng 3: Viết phương trình đường tròn tiếp xúc với đường thẳng
=> Phương pháp giải: Dựa vào tính chất tiếp tuyến
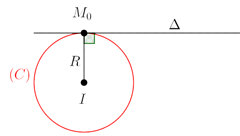
- Nếu đường tròn (C) tiếp xúc được với đường thẳng (\(\Delta\)) thì \(d(I,\Delta)=R\)
- Nếu đường tròn (C) tiếp xúc được với đường thẳng (\(\Delta\)) tại điểm A thì \(d(I,\Delta)=IA=R\)
- Nếu đường tròn (C) tiếp xúc được với hai đường thẳng (\(\Delta_1\)) và (\(\Delta_2\)) thì \(d(I,\Delta_1)=R = d(I,\Delta_2)=R\)
=> Ví dụ: Lập phương trình đường tròn (C) khi có tâm I là (2;5) và tiếp xúc với trục hoành Ox
=> Lời giải:
- Phương trình của Ox là y = 0
- Khoảng các từ I đến Ox là bán kính R của đường tròn: \(R = d(I;Ox) = \dfrac {\left | 5 \right |}{\sqrt{1}}=5\)
- Vậy phương trình đường tròn (C) có dạng là: \((x-2)^2+(y-5)^2=25\)
4. Dạng 4: Viết phương trình đường tròn nội tiếp tam giác
=> Phương pháp giải:
- Cách 1:
- Tinh diện tích S và nửa chu vi P của tam giác để tính được bán kính đường tròn \(r = \dfrac {S}{P}\)
- Gọi tâm đường tròn nội tiếp là I(a;b) thì khoảng cách từ I tới 3 cạnh của tam giác bằng nhau và bằng r, từ đó lập thành hệ phương trình với hai ẩn a và b.
- Từ đây giải hệ phương trình ta tìm được giá trị của a, b và phương trình đường tròn.
- Cách 2:
- Viết phương trình đường phân giác trong của hai góc trong tam giác
- Tìm giao điểm hai đường phân giác đó ta được tâm I của đường tròn
- Tính khoảng cách từ tâm I tới một cạnh bất kỳ của tam giác thì ta thu được kết quả của bán kính R
=> Ví dụ:
- Đề bài: Viết phương trình đường tròn ngoại tiếp tam giác OAB biết A(4;0) và B(0:3)
- Lời giải:
- Vì tam giác OAB vuông tại O nên tâm của đường tròn ngoại tiếp tam giác OAB là trung điểm của cạnh huyền AB => tọa độ tâm I của đường tròn nội tiếp sẽ là I (2; \(\dfrac {3}{2}\))
- Ta tính được bán kính R = A.I = \(\dfrac {5}{2}\)
- Kết luận: Ta có phương trình đường tròn ngoại tiếp tam giác OAB là: \((x-2)^2+(y-\dfrac {3}{2})^2=\dfrac {25}{4}\)
III. Bài tập phương trình đường tròn lớp 10
1. Bài tập có lời giải:
Bài 1: Phương trình nào là phương trình đường tròn, hãy tìm bán kính R và tâm I nếu có trong các phương trình sau:
a) \(2x^2 + 2y^2 -8x - 4y - 6 = 0\)
b) \(5x^2 + 4y^2 + x - 4y + 1=0\)
=> Hướng dẫn giải:
a) Phương trình: \(2x^2 + 2y^2 -8x - 4y - 6 = 0\) \(\Leftrightarrow x^2 + y^2 -4x-2y-3=0\)
- Có \(a^2+b^2-c=8>0\). Suy ra phương trình trên là phương trình đường tròn.
- Tâm I (2;1) và bán kính R = \(2\sqrt{2}\)
b) \(5x^2 + 4y^2 + x - 4y + 1=0\) không phải là phương trình đường tròn vì hai hệ số \(x^2 \) và \(y^2\) khác nhau.
Bài 2: Đường cong (\(C_m\)) có dạng \(x^2 + y^2 - 2mx - 4(m-2)y + 6- m=0\). Hãy:
a) Để (\(C_m\)) là phương trình đường tròn thì điều kiện của m là gì?
b) Giả sử khi (\(C_m\)) là phương trình đường tròn thì tọa độ tâm và bán kính theo tham số m là bao nhiêu?
=> Hướng dẫn giải:
a) Để (\(C_m\)) là phương trình đường tròn thì: \(m^2 + [2(m-2)]^2- (6-m)>0 \)
\(\Leftrightarrow m^2 + 4m^2 - 16m + 16 - 6 + m>0\)
\(\Leftrightarrow 5m^2 - 15m + 10>0\)
\(\Leftrightarrow m^2 - 3m + 2>0\)
\(\Leftrightarrow m<1\cup m>2\)
b) Với điều kiện được giả sử khi (\(C_m\)) là phương trình đường tròn thì tâm I của phương trình là \(I[m;(2m-4)]\) và bán kính \(R = \sqrt{m^2-3m+2}\)
Bài 3: Lập phương trình đường tròn (C) cho trường hợp đường tròn (C) có tâm I(-1;2) và tiếp xúc với đường thẳng (\(\Delta\)): x + 2y - 8 = 0
=> Hướng dẫn giải: (C) có tâm I (-1;2) và tiếp xúc với đường thẳng (\(\Delta\)): x + 2y - 8 = 0.
- Có: R = d(I;\(\Delta\)) = \(\dfrac {\left | -1 + 4 - 8\right |}{\sqrt{1^2+2^2}}=\dfrac {5}{\sqrt{5}}\) = \(\sqrt{5}\)
- Vậy phương trình đường tròn (C) có dạng là \((x+1)^2+(y-2)^2=5\)
Bài 4: Trong hệ tọa độ Oxy cho hai đường thẳng (d1): x + 2y - 3 = 0 và (d2): x + 3y - 5 = 0. Hãy lập phương trình đường tròn có bán kính R = \(\sqrt{10}\) có tâm thuộc (d1) và tiếp xúc với (d2)
=> Hướng dẫn giải:
- Vì tâm I thuộc d1 nên I (\(-2a+3;a\)) do (C) tiếp xúc với d2 nên ta có: d(I;d2) = R \(\Leftrightarrow \dfrac {\left | a-2 \right |}{\sqrt{10}}=\sqrt{10}\) \(\Leftrightarrow \) a = -8 hoặc a = 12
- Suy ra: \(I_1(19;-8) \ và \ I_2(-21;12)\)
- Như vậy có hai phương trình đường tròn thỏa mãn điều kiện:
- \((C_1): (x-19)^2+(y+8)^2=10\)
- \((C_2): (x+21)^2+(y-12)^2=10\)
2. Bài tập tự luyện (không lời giải)
Bài 1: Cho phương trình (C): \(x^2 + y^2 -2xcos\alpha - 2ysin\alpha + cos2\alpha = 0 (\alpha \neq k\pi)\)
a) Hãy chứng minh phương trình (C) là phương trình đường tròn
b) Để phương trình (C) có bán kính lớn nhất thì \(\alpha\) bằng bao nhiêu?
c) Tìm quỹ tính tâm I của (C)
Bài 2: Lập phương trình đường tròn cho các trường hợp sau đây:
a) Đường kính AB, trong đó A (1;1) và B (5;3)
b) Đi qua A (-1;3); B (3;5); C (4;-2)
=> Gợi ý đáp án:
a) \((x-3)^2+(y-2)^2=5\)
b) \(x^2 + y^2 - \dfrac {14}{3}x - \dfrac {8}{3}y - \dfrac {20}{3}=0\)
Bài 3: Cho ba đường thẳng: (d1): \(4x - 3y - 65 = 0\); (d2): \(7x - 24y + 55 = 0\)l; (d3): \(3x + 4y - 5 =0\). Hãy lập phương trình đường tròn nội tiếp tam giác ABC được tạo bởi ba đường thẳng trên.
=> Gợi ý đáp án: \((x-10)^2+y^2=25\)
Bài 4: Hai đường thẳng (d1): x + 2y - 8 = 0 và (d2): 2x + y + 5 = 0 thuộc trong hệ tọa độ Oxy. Hãy viết phương trình đường tròn có tâm nằm trên đường thẳng (d): x - 2y + 1 = 0 tiếp xúc với hai đường thẳng (d1) và (d2).
=> Gợi ý đáp án: Có hai đường tròn thỏa mãn điều kiện
- Phương trình đường tròn (C1): \((x+25)^2 + (y+12)^2 = \dfrac {57}{5}\)
- Phương trình đường tròn (C2): \((x-\dfrac {1}{2})^2 + (y - \dfrac {2}{3})^2 = \dfrac {361}{45}\)
Xem thêm >>> Giải bài tập SGK Phương trình đường tròn lớp 10
Trên đây là những dạng công thức phương trình đường tròn lớp 10 và các dạng bài tập chuyên đề phương trình đường tròn lớp 10 mà Cunghocvui muốn gửi đến các bạn. Thấy hay đừng quên like và share, chúc các bạn học tập tốt <3
Tags phương trình đường tròn lớp 10 bài tập phương trình đường tròn lớp 10 các dạng phương trình đường tròn lớp 10 công thức phương trình đường tròn lớp 10 bài tập chuyên đề phương trình đường tròn lớp 10Từ khóa » Cách Tính R Trong đường Tròn
-
Lý Thuyết Phương Trình đường Tròn | SGK Toán Lớp 10
-
§2. Phương Trình đường Tròn - Hoc24
-
Phương Trình đường Tròn: Lý Thuyết, Công Thức Và Cách Giải Các Dạng ...
-
Phương Trình đường Tròn: Lý Thuyết, Công Thức, Cách Giải Các Dạng ...
-
Tổng Hợp Các Công Thức Tính Bán Kính Đường Tròn Lớp 10 ...
-
Công Thức Tính R Hình Tròn - Học Tốt
-
Tìm Tâm Và Bán Kính đường Tròn
-
Công Thức Phương Trình đường Tròn Và Bài Tập Có Lời Giải Chi Tiết
-
Lý Thuyết Phương Trình đường Tròn Hay, Chi Tiết - Lớp 10
-
Chia Sẽ Phương Trình Và Công Thức đường Tròn đơn Giản
-
Lý Thuyết đường Tròn Lớp 9 đầy đủ Nhất - Abcdonline
-
Cách để Tính Bán Kính Đường Tròn - WikiHow
-
Giải Toán 10 Bài 2. Phương Trình đường Tròn
-
Bài 2. Phương Trình đường Tròn - Củng Cố Kiến Thức