Phương Trình Và Hệ Phương Trình Bậc Nhất Ba ẩn – Bài Tập Vận Dụng

Lý thuyết về phương trình và hệ phương trình bậc nhất ba ẩn – Bài tập vận dụng

1. Phương trình bậc nhất ba ẩn

Phương trình bậc nhất ba ẩn có dạng tổng quát là:

ax + by + cz = d

Trong đó:

x, y, z là 3 ẩn

a, b, c, d là các hệ số và a, b, c, d không đồng thời bằng 0.

Ví dụ:

2x + y + z = 0

x – y = 6

3y = 5

2. Hệ phương trình bậc nhất ba ẩn

Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là:

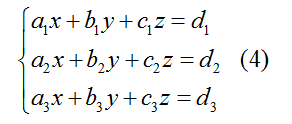Trong đó x, y, z là ba ẩn; a1, b1, c1, a2, b2, c2, a3, b3, c3 , d1, d2, d3 là các hệ số.

Mỗi bộ ba số ( x0, y0, z0 ) nghiệm đúng cả ba phương trình được gọi là một nghiệm của hệ phương trình (4).

3. Phương pháp giải hệ phương trình bậc nhất ba ẩn

Giaỉ hệ phương trình (4) là tìm tất cả các bộ ba số (x, y, z) đồng thời nghiệm đúng cả 3 phương trình của hệ.

Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để quy về giải hệ phương trình có ít ẩn số hơn.

Để khử bớt ẩn, ta cũng có thể dùng các phương pháp cộng đại số hay phương pháp thế giống như đối với hệ phương trình bậc nhất hai ẩn.

Ví dụ 1: Giải hệ phương trình sau:

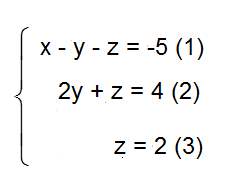
Bài giải

– Thế z = 2 vào pt (2) ta được 2y + 2 = 4 <=> 2y = 2 <=> y = 1

– Thế z = 2, y = 1 vào pt(1) ta được x – 1 – 2 = -5 <=> x = -2

Vậy hệ phương trình đã cho có nghiệm là: ( -2, 1, 2)

Ví dụ 2: Giải hệ phương trình

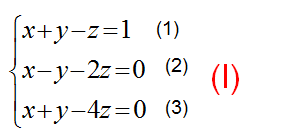
Ta có thể đưa hệ phương trình về dạng tam giác bằng cách khử ẩn số (khử ẩn x ở pt(2) rồi khử ẩn x và y ở pt(3), …). Dùng phương pháp cộng đại số giống như hệ hai phương trình bậc nhất hai ẩn.

Bài giải:

Trừ từng vế của pt(1) và pt(2) ta được hệ pt:

Trừ từng vế của pt(1) và pt(3) ta được hệ pt:

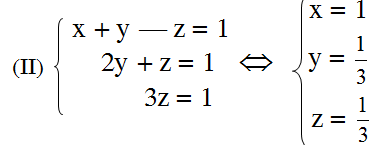
Vậy hệ phương trình đã cho có nghiệm là:

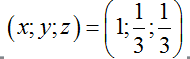
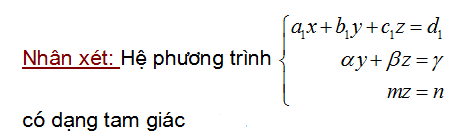
Nhận xét: Để giải một hệ phương trình bậc nhất ba ẩn ta thường biến đổi hpt đã cho về dạng tam giác bằng phương pháp khử dần ẩn số (phương pháp Gau-Xơ )

Ví dụ 3: Giải hệ phương trình (II) bằng máy tính bỏ túi

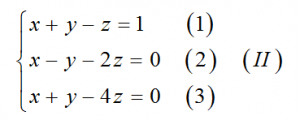
Hướng dẫn giải:

Ví dụ 4: Giải hệ phương trình sau bằng phương pháp Gau-Xơ và bằng máy tính bỏ túi.

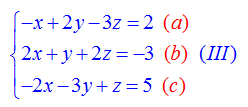
Nhân hai vế của  pt (a) cho 2 rồi cộng với pt (b) theo từng vế; nhân hai vế của pt (a) cho (-2) rồi cộng với pt (c) theo từng vế ta được:

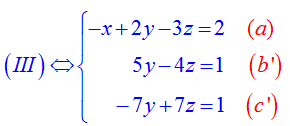
Nhân hai vế của pt (b’) cho 7 và nhân hai vế của pt (c’) cho 5 rồi cộng lại theo từng vế tương ứng ta được:

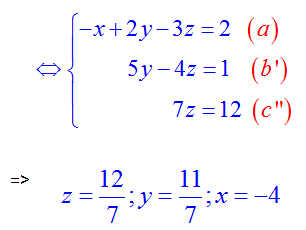
Vậy nghiệm của hpt (III) là:

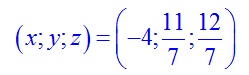
Ví dụ 5. Dùng máy tính bỏ túi giải các hệ phương trình sau:

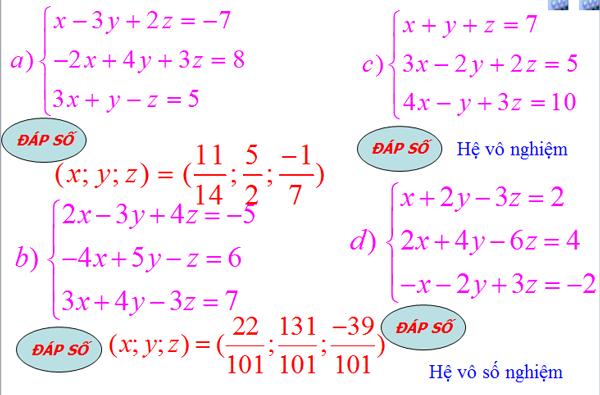
Gợi ý :

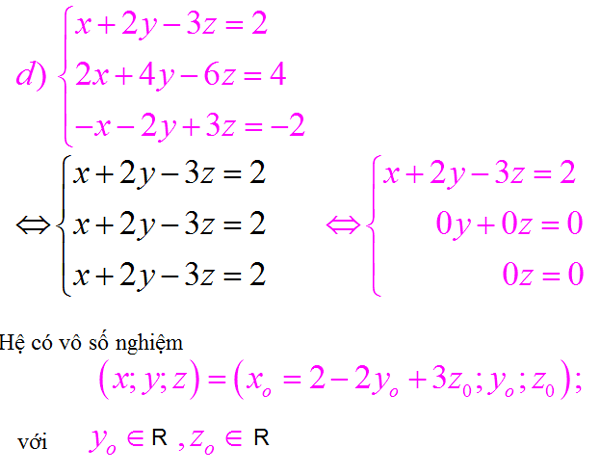
Ví dụ 6. Bài tập thực tiễn

Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu 5.349.000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu 5.259.000 đồng. Hỏi giá bán mỗi áo, mỗi quần và mỗi váy là bao nhiêu?

Bài giải:

Đặt x, y, z  tương ứng là giá bán của mỗi áo sơ mi, mỗi quần âu nam, mỗi váy nữ. ( Đơn vị tính là ngàn đồng ). ĐK: x>0, y>0, z>0

Ví dụ 7: Gỉai hpt sau:

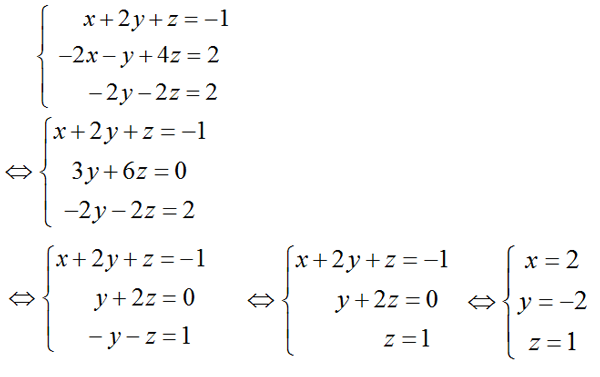
Vậy nghiệm của hpt đã cho bằng (x, y, z) = (2, -2, 1).

Trên đây là công thức giải phương trình và hệ phương trình bậc nhất ba ẩn và bài tập áp dụng. Chúc các em học tốt!