Prove The Identities Below: Sinh (x+y) Sinhx Coshy Coshx ... - Numerade

This problem has been solved by verified expert Pritesh Ranjan 100% free to try - get full access instantly Start Free Trial

Question

Prove the identities below: sinh (x+y) = sinhx coshy + coshx sinhy cosh (x-y) = coshxcosh sinh x sinh y Then use them to show the following: sinh Zx 2 = sinh_ coshx cosh 2x = cosh X+ sinh Start by proving the first identity: sinh (x+y) = sinhxcoshy - coshx sinhy Use the fact that sinhx = exponential Rewrite the left side sinh (x +y), using In 2x sinh (x+y) Substitute_ Prove the identities below: sinh (x+y) = sinhx coshy + coshx sinhy cosh (x-y) = coshxcosh sinh x sinh y Then use them to show the following: sinh Zx 2 = sinh_ coshx cosh 2x = cosh X+ sinh Start by proving the first identity: sinh (x+y) = sinhxcoshy - coshx sinhy Use the fact that sinhx = exponential Rewrite the left side sinh (x +y), using In 2x sinh (x+y) Substitute_ Show more…

Added by Zachary W.

Close

Calculus: Early Transcendentals James Stewart 8th Edition

Step 1

Now, let's find sinh(x+y): sinh(x+y) = (e^(x+y) - e^(-(x+y)))/2 = (e^x * e^y - e^(-x) * e^(-y))/2 Now let's find sinh(x)cosh(y) + cosh(x)sinh(y): sinh(x)cosh(y) + cosh(x)sinh(y) = (e^x - e^(-x))/2 * (e^y + e^(-y))/2 + (e^x + e^(-x))/2 * (e^y - Show more…

Show all steps

Close

Please give Ace some feedback

Your feedback will help us improve your experience

Submit Thanks for your feedback! Prove the identities below: sinh (x+y) = sinhx coshy + coshx sinhy cosh (x-y) = coshxcosh sinh x sinh y Then use them to show the following: sinh Zx 2 = sinh_ coshx cosh 2x = cosh X+ sinh Start by proving the first identity: sinh (x+y) = sinhxcoshy - coshx sinhy Use the fact that sinhx = exponential Rewrite the left side sinh (x +y), using In 2x sinh (x+y) Substitute_ Play audio Feedback Powered by NumerAI

Pritesh Ranjan and 81 other Calculus 1 / AB educators are ready to help you.

Ask a new question

Key Concepts

Key Concept Premium Feature Explore the core concept behind this problem. View Video View Video Key Concept Premium Feature Explore the core concept behind this problem. Your browser does not support the video tag. Close Try it Now

Recommended Videos

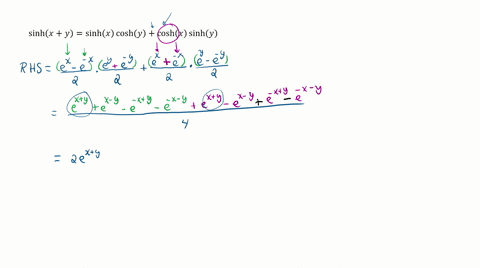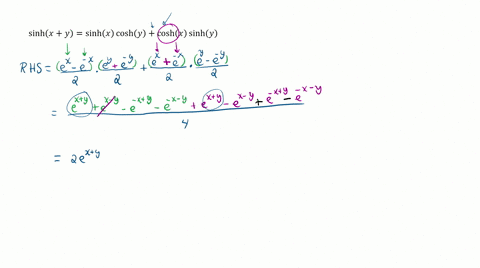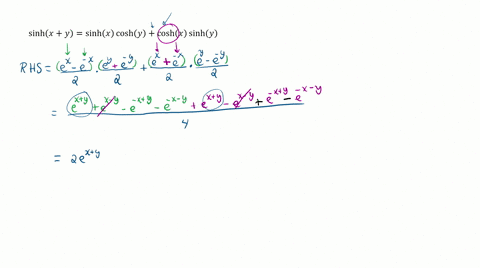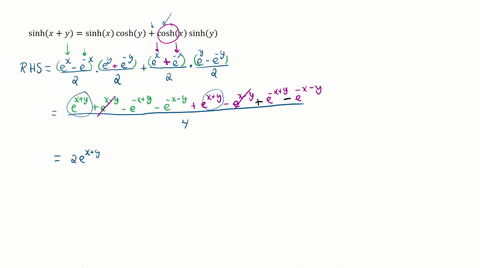
Prove the identities $\begin{aligned} \sinh (x+y) &=\sinh x \cosh y+\cosh x \sinh y \\ \cosh (x+y) &=\cosh x \cosh y+\sinh x \sinh y \end{aligned}$ Then use them to show that a. \sinh 2 x=2 \sinh x \cosh x b. \cosh 2 x=\cosh ^{2} x+\sinh ^{2} x

Transcendental Functions

Hyperbolic Functions

Prove the identities $$\begin{aligned} \sinh (x+y) &=\sinh x \cosh y+\cosh x \sinh y \\ \cosh (x+y) &=\cosh x \cosh y+\sinh x \sinh y \end{aligned}$$ Then use them to show that \begin{equation}\begin{array}{l}{\text { a. } \sinh 2 x=2 \sinh x \cosh x} \\ {\text { b. } \cosh 2 x=\cosh ^{2} x+\sinh ^{2} x}\end{array}\end{equation}

Transcendental Functions

Hyperbolic Functions

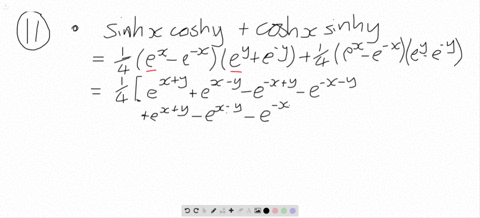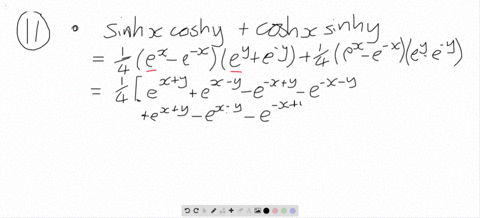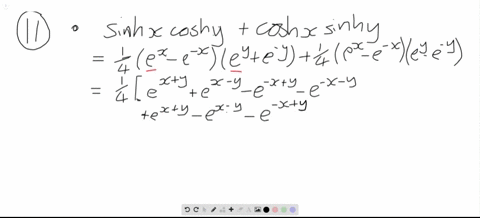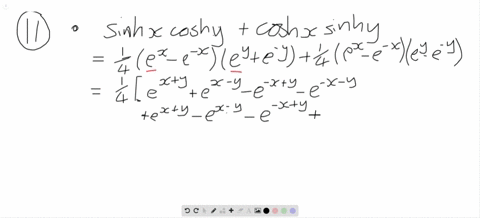
Prove the identities $$\begin{array}{l} \sinh (x+y)=\sinh x \cosh y+\cosh x \sinh y, \\ \cosh (x+y)=\cosh x \cosh y+\sinh x \sinh y. \end{array}$$ Then use them to show that a. $\sinh 2 x=2 \sinh x \cosh x.$ b. $\cosh 2 x=\cosh ^{2} x+\sinh ^{2} x.$

Integrals and Transcendental Functions

Hyperbolic Functions

Recommended Textbooks

Calculus: Early Transcendentals

James Stewart 8th Edition 1,733 solutions

Calculus: Early Transcendentals

William Briggs, Lyle Cochran, Bernard Gillet 3rd Edition 1,120 solutions

Thomas Calculus

George B. Thomas Jr. 14th Edition 1,879 solutions Need help? Use Ace Ace is your personal tutor. It breaks down any question with clear steps so you can learn. Start Using Ace Ace is your personal tutor for learning Step-by-step explanations Instant summaries Summarize YouTube videos Understand textbook images or PDFs Study tools like quizzes and flashcards Listen to your notes as a podcast

What our educators say

25992 Students Helped in Calculus 1 / AB “Numerade has a great goal - to increase people's educational levels all around the world. Educators do not complete student's personal homework tasks. We create video tutorials that may be used for many years in the future.” Dr. Mei Lin Chen PhD in Calculus 1 / AB

44601 Students Helped in Calculus 1 / AB "The format has forced me to think about what knowledge is needed by the student to solve a problem and present it concisely and understandably within the time constraint of the video." Dr. Emily Green PhD in Calculus 1 / AB

30417 Students Helped in Calculus 1 / AB “Explaining topics while I make Numerade videos has helped me deepen my own understanding and come up with new ways to help my students grasp concepts while I'm teaching.” Professor Jonathan Reed Master's in Calculus 1 / AB

Get step-by-step video solutionfrom top educators Start your free 7-day trial, Sign up now. Continue with Facebook Continue with Apple Continue with Clever or Name Email Password Create Account By creating an account, you agree to the Terms of Service and Privacy Policy Already have an account? Log In A free answerjust for you

Watch the video solution with this free unlock.

View the Answer

Log in to watch this video ...and 100,000,000 more!

EMAIL

PASSWORD

Log in OR Continue with Facebook Continue with Apple Continue with Clever Don't have an account? Sign Up