Quá Trình đẳng áp – Wikipedia Tiếng Việt
Có thể bạn quan tâm
| Nhiệt động lực học | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Động cơ nhiệt Carnot cổ điển Động cơ nhiệt Carnot cổ điển | |||||||||||||||||||||
Các nhánh
| |||||||||||||||||||||
Nguyên lý
| |||||||||||||||||||||
Hệ thống nhiệt động
| |||||||||||||||||||||
Thuộc tính hệNote: Biến số liên hợp in italics
| |||||||||||||||||||||
Tính năng vật liệu
| |||||||||||||||||||||
Phương trình
| |||||||||||||||||||||
Thế nhiệt động
| |||||||||||||||||||||
| |||||||||||||||||||||
Nhà khoa học
| |||||||||||||||||||||
| Sách | |||||||||||||||||||||
|
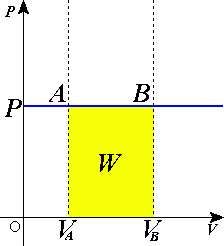
Quá trình đẳng áp (tiếng Anh: isobaric process) là 1 quá trình nhiệt động lực học trong đó áp suất là 1 hằng số (không đổi theo thời gian). Theo nguyên lý 1 nhiệt động lực học:
Theo định luật 1 về nhiệt động lực học, nếu thể tích của khí tăng lên thì công được sinh ra do sự dãn ra (tăng thể tích) của khí, cụ thể như sau:
Trong chất khi lý tưởng: trong đó n là số mol khí, R là hằng số khí lý tưởng
nên [1]
Vậy ta có được biểu thức
Liên hệ giữa nhiệt dung mol đẳng tích và đẳng áp
[sửa | sửa mã nguồn]Dựa vào quá trình đẳng tích, giữa quá trình không có sự truyền nhiệt của các phản ứng hóa học, ta thu được sự liên hệ giữa độ thay đổi nội năng phụ thuộc vào nhiệt độ như sau: với là nhiệt dung mol khi thể tích không đổi [2] Với là số bậc tự do của phân tử khí Khi áp suất không đổi, với là nhiệt dung mol khi áp suất không đổi.
Từ định luật 1 nhiệt động lực học ta có:
Tham khảo
[sửa | sửa mã nguồn]- ^ "Patana". Bản gốc lưu trữ ngày 4 tháng 7 năm 2011. Truy cập ngày 10 tháng 7 năm 2012. {{Chú thích web}}: Đã bỏ qua tham số không rõ |= (trợ giúp)
- ^ Principles of Physics, trang 621
Bài viết về chủ đề vật lý này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn. |
- x
- t
- s
Từ khóa » Công Thức Tính Công Trong Quá Trình đẳng áp
-
Quá Trình đẳng áp- Định Luật Gay Luyxac
-
Bài Tập Nguyên Lí I, Nguyên Lí II Nhiệt động Lực Học - Vật Lí Phổ Thông
-
Quá Trình đẳng áp, Phương Trình Trạng Thái Của Khí Lí Tưởng Và Bài Tập
-
Công Khí Thực Hiện Trong Quá Trình đẳng áp Là?
-
Công Thức Cho Quá Trình đẳng áp Là Gì - Vật Lí Lớp 10
-
Công Thức Quá Trình đẳng áp
-
Lý Thuyết Và Tổng Hợp Công Thức Vật Lý 10 Chương 5-6 Bạn Cần ...
-
Công Thức đẳng áp - Xây Nhà
-
Quá Trình đẳng áp, Phương Trình Trạng Thái Của Khí Lí Tưởng Và Bài ...
-
Bài 59: Áp Dụng Nguyên Lí I Nhiệt động Lực Học Cho Khí Lí Tưởng
-
Công Thức Tính Công Trong Quá Trình đẳng Nhiệt - Cùng Hỏi Đáp
-
VL1 Tổng Hợp Cong Thức Va Giải Một Số Bai Tập Chương 4 5
-
Nguyên Lý Nhiệt ðộng Lực Học
-
[PDF] Dãn Nở đẳng Nhiệt (Ti=Tz)






























