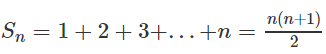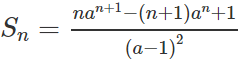S N = 1 + 2 . A + 3 . A 2 + . . . + N . A N - 1 - B) Sn=1.x+2 ...

× Đăng nhập Facebook Google ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

22/07/2024 802

Tính tổng :

a) Sn=1+2.a+3.a2+...+n.an-1

b) Sn=1.x+2.x2+3.x3+...+n.xn

Xem lời giải Câu hỏi trong đề: Giải SBT Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

a) Với a = 1 ta có

Giả sử a ≠ 1. Nhân hai vế của hệ thức

Sn=1+2.a+3.a2+...+n.an-1 với a và tính hiệu

Sn-a.Sn=(1-a).Sn

Từ đó, ta tính được

b) Làm tương tự như câu a).

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho dãy số

(un): u1=1, u2=2un+1=2un-un-1+1với n≥2

a) Viết năm số hạng đầu của dãy số ;

b) Lập dãy số (vn) với vn=un+1-un. Chứng minh dãy số (vn) là cấp số cộng ;

c) Tìm công thức tính (un) theo n.

Xem đáp án » 18/12/2021 9,798

Câu 2:

Cho dãy số (un):

u1=13un+1=(n+1)un3n vơi n≥1

a) Viết năm số hạng đầu của dãy số.

b) Lập dãy số (vn) với vn=unn . Chứng minh dãy số (vn) là cấp số nhân.

c) Tìm công thức tính (un) theo n.

Xem đáp án » 18/12/2021 4,409

Câu 3:

Chứng minh rằng nếu ba số lập thành một cấp số nhân, đồng thời lập thành cấp số cộng thì ba số ấy bằng nhau.

Xem đáp án » 18/12/2021 527

Câu 4:

Cho cấp số nhân (un) có công bội là q và các số hạng là chẵn. Gọi Sc là tổng các số hạng có chỉ số chẵn và Sl

là tổng các số hạng có chỉ số lẻ. Chứng minh rằng : q=ScSl

Xem đáp án » 18/12/2021 385

Câu 5:

Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820?

Xem đáp án » 18/12/2021 364

Câu 6:

Chứng minh rằng

a) n5-n chia hết cho 5 với mọi n∈ℕ*;

b) Tổng các lập phương của ba số tự nhiên liên tiếp chia hết cho 9 ;

c) n3-n chia hết cho 6 với mọi n∈ℕ*;

Xem đáp án » 18/12/2021 361

Câu 7:

Một cấp số cộng và một cấp số nhân có số hạng thứ nhất bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ ba bằng nhau. Tìm các cấp số ấy.

Xem đáp án » 18/12/2021 347

Câu 8:

Chứng minh các đẳng thức sau với n∈ℕ*

a) An=11.2.3+12.3.4+...+1n(n+1)(n+2)=n(n+3)4(n+1)(n+2);

b) Bn=1+3+6+10+...+n(n+1)2=n(n+1)(n+2)6;

c) Sn=sinx+sin2x+sin3x+...+sinnx=sinnx2.sin(n+1)x2sinx2

Xem đáp án » 18/12/2021 341

Câu 9:

Tính tổng:

a) 12+322+523+...+2n-12n;

b) 12-22+32-42+...+(-1)n-1.n2

Xem đáp án » 18/12/2021 336

Câu 10:

Có thể có một tam giác vuông mà số đo các cạnh của nó lập thành một cấp số cộng không ?

Xem đáp án » 18/12/2021 279

Câu 11:

Chứng minh các bất đẳng thức sau

a) 3n − 1 > n(n + 2) với n ≥ 4 ;

b) 2n − 3 > 3n − 1 với n ≥ 8

Xem đáp án » 18/12/2021 227

Câu 12:

Tìm m để phương trình x4-(3m+5)x2+(m+1)2=0 có bốn nghiệm lập thành cấp số cộng.

Xem đáp án » 18/12/2021 224 Xem thêm các câu hỏi khác » Hỏi bài

Đề thi liên quan

Xem thêm »

• Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 30405 lượt thi Thi thử
• Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 10072 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 6509 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 6202 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 6184 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 4856 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 4658 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 4424 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng (có đáp án) 9 đề 4100 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 4053 lượt thi Thi thử

Xem thêm »