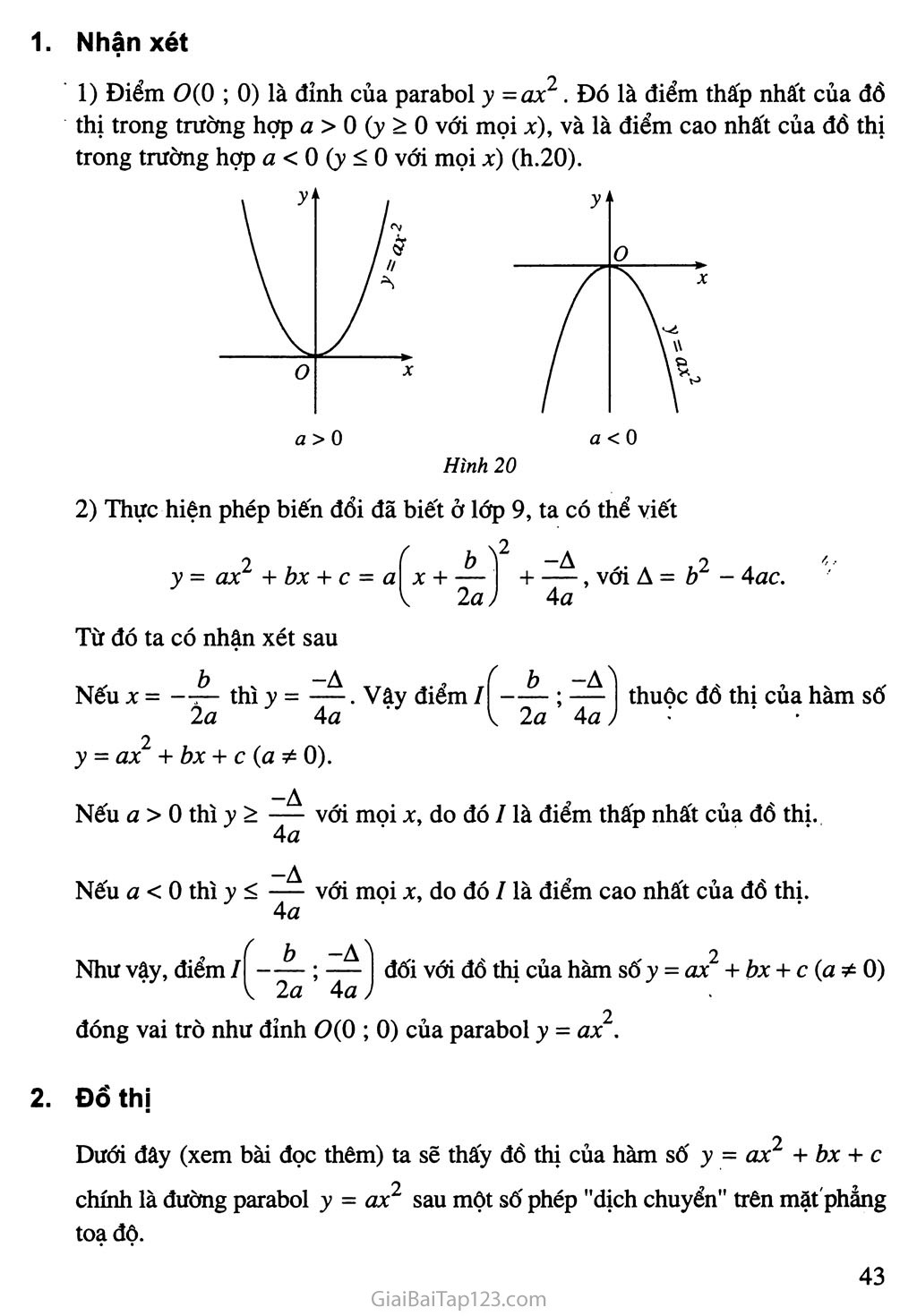
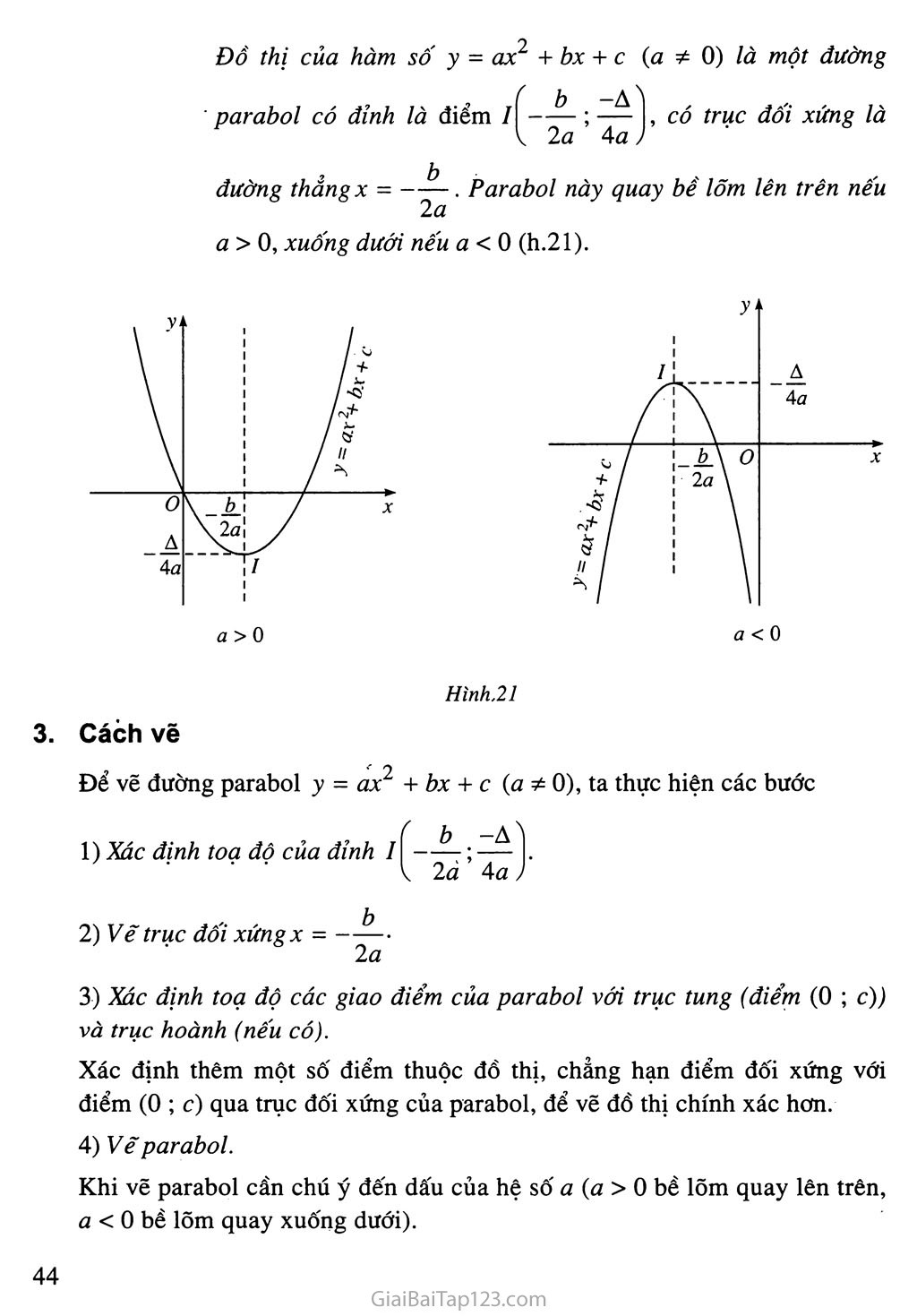
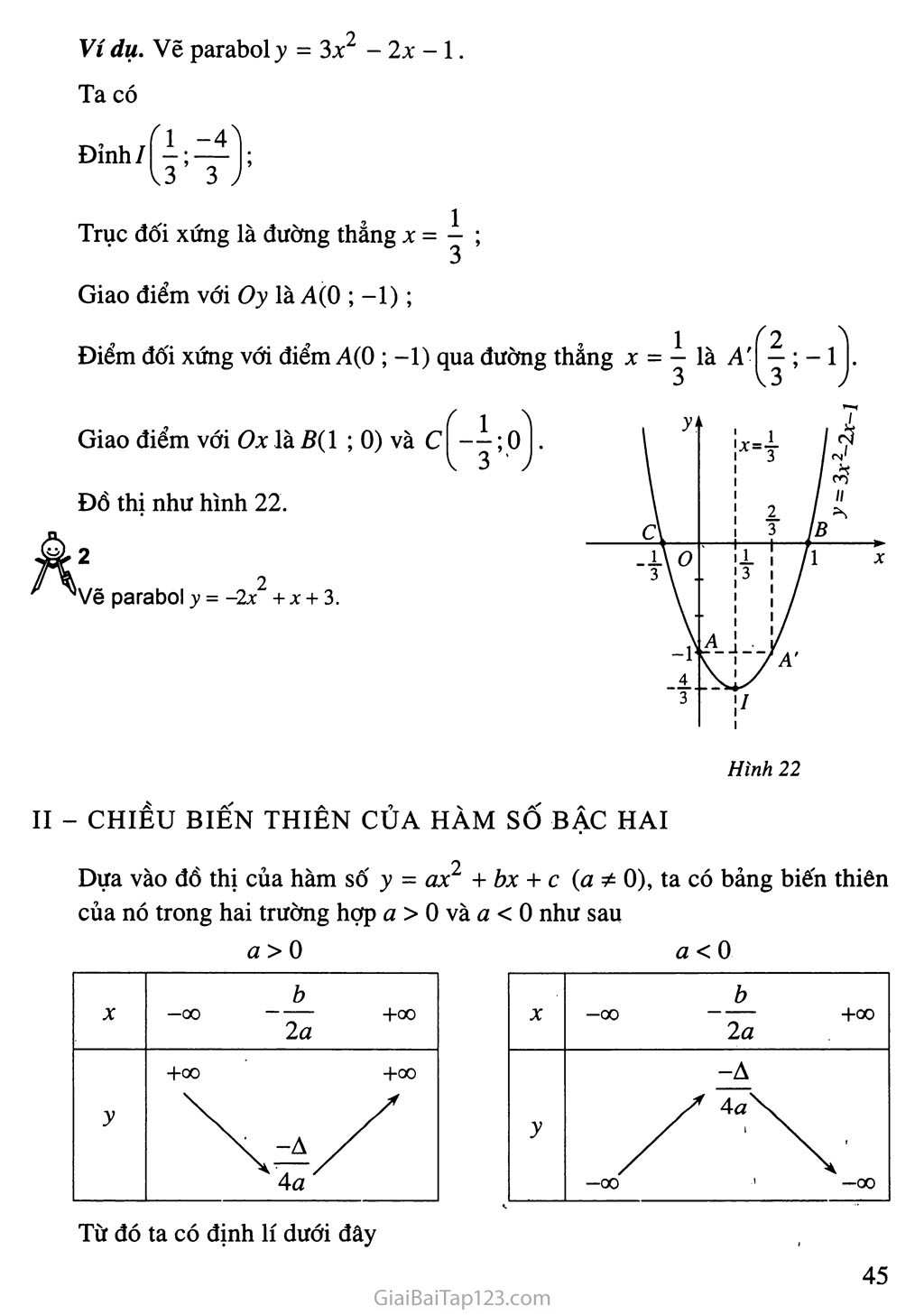
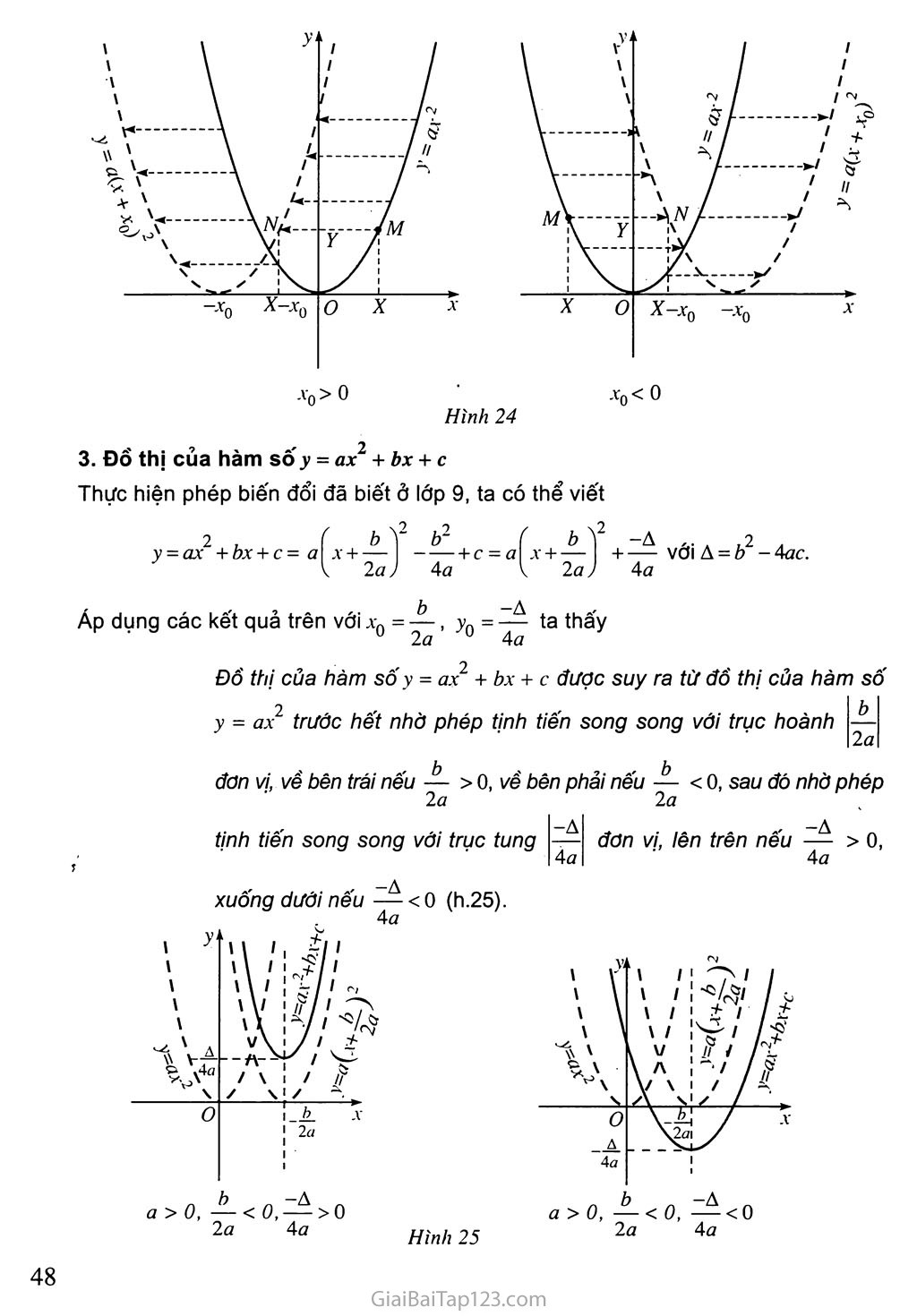
SGK Đại Số 10 - Bài 3. Hàm Số Bậc Hai

• Home
• Lớp 1,2,3
  • Lớp 1
  • Giải Toán Lớp 1
  • Tiếng Việt Lớp 1
  • Lớp 2
  • Giải Toán Lớp 2
  • Tiếng Việt Lớp 2
  • Văn Mẫu Lớp 2
  • Lớp 3
  • Giải Toán Lớp 3
  • Tiếng Việt Lớp 3
  • Văn Mẫu Lớp 3
  • Giải Tiếng Anh Lớp 3
• Lớp 4
  • Giải Toán Lớp 4
  • Tiếng Việt Lớp 4
  • Văn Mẫu Lớp 4
  • Giải Tiếng Anh Lớp 4
• Lớp 5
  • Giải Toán Lớp 5
  • Tiếng Việt Lớp 5
  • Văn Mẫu Lớp 5
  • Giải Tiếng Anh Lớp 5
• Lớp 6
  • Soạn Văn 6
  • Giải Toán Lớp 6
  • Giải Vật Lý 6
  • Giải Sinh Học 6
  • Giải Tiếng Anh Lớp 6
  • Giải Lịch Sử 6
  • Giải Địa Lý Lớp 6
  • Giải GDCD Lớp 6
• Lớp 7
  • Soạn Văn 7
  • Giải Bài Tập Toán Lớp 7
  • Giải Vật Lý 7
  • Giải Sinh Học 7
  • Giải Tiếng Anh Lớp 7
  • Giải Lịch Sử 7
  • Giải Địa Lý Lớp 7
  • Giải GDCD Lớp 7
• Lớp 8
  • Soạn Văn 8
  • Giải Bài Tập Toán 8
  • Giải Vật Lý 8
  • Giải Bài Tập Hóa 8
  • Giải Sinh Học 8
  • Giải Tiếng Anh Lớp 8
  • Giải Lịch Sử 8
  • Giải Địa Lý Lớp 8
• Lớp 9
  • Soạn Văn 9
  • Giải Bài Tập Toán 9
  • Giải Vật Lý 9
  • Giải Bài Tập Hóa 9
  • Giải Sinh Học 9
  • Giải Tiếng Anh Lớp 9
  • Giải Lịch Sử 9
  • Giải Địa Lý Lớp 9
• Lớp 10
  • Soạn Văn 10
  • Giải Bài Tập Toán 10
  • Giải Vật Lý 10
  • Giải Bài Tập Hóa 10
  • Giải Sinh Học 10
  • Giải Tiếng Anh Lớp 10
  • Giải Lịch Sử 10
  • Giải Địa Lý Lớp 10
• Lớp 11
  • Soạn Văn 11
  • Giải Bài Tập Toán 11
  • Giải Vật Lý 11
  • Giải Bài Tập Hóa 11
  • Giải Sinh Học 11
  • Giải Tiếng Anh Lớp 11
  • Giải Lịch Sử 11
  • Giải Địa Lý Lớp 11
• Lớp 12
  • Soạn Văn 12
  • Giải Bài Tập Toán 12
  • Giải Vật Lý 12
  • Giải Bài Tập Hóa 12
  • Giải Sinh Học 12
  • Giải Tiếng Anh Lớp 12
  • Giải Lịch Sử 12
  • Giải Địa Lý Lớp 12

Trang Chủ › Lớp 10› Giải Bài Tập Toán 10› Sách Giáo Khoa - Đại Số 10› Bài 3. Hàm số bậc hai SGK Đại Số 10 - Bài 3. Hàm số bậc hai

• 
• 
• 
• 
• 
• 
• 
• 
• 

I - Hàm số bậc hai được cho bởi công thức 2 y = ax + bx + c (ữ*0). Tập xác định của hàm số này là D = R. 2 Hàm số y = ax (ứ 0) đã học ở lớp 9 là một trường hợp riêng của hàm số này. I - ĐỒ THỊ CỦA HÀM số BẬC HAI 1 Nhắc lại các kết quả đã biết về đổ thị của hàm số y = Nhận xét Điểm ơ(0 ; 0) là đỉnh của parabol y -ax2. Đó là điểm thấp nhất của đồ thị trong trường hợp a > 0 (y > 0 với mọi x), và là điểm cao nhất của đồ thị trong trường hợp ứ < 0 (y < 0 với mọi x) (h.20). Thực hiện phép biến đổi đã biết ở lớp 9, ta có thể viết 2 I í b ý2 —A x 2 . y = ax + bx + c = a\x + -z—\ + —,vớiA=ồ - 4ưc. I 2a) 4ư Từ đó ta có nhận xét sau Nếu X = -ỉ- thì y = ~. Vậy điểm I\ -Ạ-; —— I thuộc đồ thị của hàm số 2a 4ứ < 2a 4ớ) 2 y = ax + bx + c (a *0). Nếu a > 0 thì y > —với mọi X, do đó I là điểm thấp nhất của đồ thị. 4ứ Nếu a < 0 thì y < —với mọi X, do đó I là điểm cao nhất của đồ thị. 4a Như vậy, điểm /í ~1 đối với đồ thị của hàm số y = ax2 + bx + c(a*ơ) V 2a 4ứ) đóng vai trò như đỉnh ớ(0 ; 0) của parabol y = ax . 2. Đồ thị Dưới đây (xem bài đọc thêm) ta sẽ thấy đồ thị của hàm số y = ax2 + bx + c chính là đường parabol y = ÍZX2 sau một số phép "dịch chuyển" trên mặt phẳng toạ độ. Đồ thị của hàm số y = ax~ + bx + c (a 0) là một đường parabol có đỉnh là điểm l\ , có trục đối xứng là V 2a 4u / đường thẳng x = . Parabol này quay bề lõm lên trên nếu la a>0, xuống dưới nếu a < 0 (h.21). Hình.21 Cách vẽ Để vẽ đường parabol y - ax2 + bx + c (ữ 0), ta thực hiện các bước Xác định toạ độ của đỉnh I\ --T-; —— |. Vẽ trục đối xứngx = -■ 2a Xác định toạ độ các giao điểm của parabol với trục tung (điểm (0 ; c)) và trục hoành (nếu có). Xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm (0 ; c) qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn. Vẽparabol. Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới). Ví dụ. Vẽ parabola = 3%2 - 2x - 1. Ta có Đỉnh4^) Trục đối xứng là đường thẳng X - Giao điểm với Oy là Â(0 ; -1) ; II - CHIỀU BIẾN THIÊN CỦA HÀM số BẬC HAI Dựa vào đồ thị của hàm số V = ax + bx + c (a 0), ta có bảng biến thiên < 0 như saụ của nó trong hai trường hợp a > 0 và Từ đó ta có định lí dưới đây ĐỊNH LÍ (Nếu a > 0 thì hàm số y - ax2 + bx + c 2ứ Đồng biến trên khoảng 4;+4 Nếu a < 0 thì hàm số y = CCC + bx + c -b Đồng biến trên khoảng Nghịch biến trên khoảng —00 2a -ồ 2ứ BÀI ĐỌC THÊM ĐƯỜNG PARABOL Trong §3, ta đã khẳng định rằng đồ thị của hàm số bậc hai y = ax2 + bx + c (a 0) là một đường parabol. Dưới đây ta sẽ chứng tỏ điều đó và cho thấy đường parabol này được suy ra từ parabol y = ax2 như thê' nào. 1. Đố thị cúa ham so y = ax +y0 Xét hai hàm sốf[x) = ax2 và g(x) = ax2 + >Q. Tại cùng một điểm Xe R ta có Y = fựỉ) = aX2 , g(X) = aX2 +yữ = Y + yữ. Do đó, nếu điểm M(X; Y) thuộc đồ thị của hàm sô' y = ax2 thì điểm N(X ',Y + yữ) thuộc đồ thị của hàm sô' y = ax2 + yữ. Ta thấy nếu dịch chuyển (tịnh tiến) điểm M(x; Y) song song với trục tung một đoạn bằng jy0| đơn vị (lên trên nếu y0 > 0, xuống dưới nếu y0 < 0) thì được điểm N(X;K + y0). Nghịch biến trên khoảng -co; Vậy Đồ thị của hàm sô'y = ax' + >’o nhận được từ đồ thị của hàm sô' y = ax2 nhờ phép tịnh tiến song song với trục tung lyol đơn vị, lên trên nếu y0 > 0, xuống dưới nếuyữ < 0 (h.23). Hình 23 Đồ thị của hàm sốy = a(x + x0)2 Xét hai hàm sô' /(x) = ax~ và g(x) = a(x + x0)2. Với xtuỳ ý, ta có f(X) = aX2 , g(X-x0) = a[(X-x0) + x0]2 = aX2 . Nghĩa là, giá trị của hàm số/(x) tại Xbằng giá trị của hàm sô' g(x) tại X- XQ. Vậy nếu điểm M(X; Y) thuộc đồ thị của hàm sốy = ax2 thì điểm NỰỈ-xq ; Y) thuộc đồ thị của hàm sốy = a(x + x0)2. Ta thấy, nếu tịnh tiến điểm Mựỉ; y) song song với trục hoành |x0| đơn vị về bên trái nếu x0 > 0, về bên phải nếu x0 < 0 thì được điểm N(X-xữ ; y). Vậy Đồ thị của hàm sô y = í/(x + Xg) nhập được từ đồ thị của hàm sô y = ax nhờ phép tịnh tiến song song với trục hoành |x0| đơn vị, về bên trái nếu x0 > 0, về bên phải nếu x0 < 0 (h.24). x0 > 0 ' -Vo < 0 Hình 24 3. Đồ thị của hàm sốy = ax2 + bx + c Thực hiện phép biến đổi đã biết ở lớp 9, ta có thể viết tịnh tiến song song với trục tung -A 4ứ đơn vị, lên trên nếu — > 0, 4ữ Như vậy, đổ thị của hàm số bậc hai ỵ = ax2 + bx + c cũng là một đường parabol. Trong đời sống hằng ngày chúng ta thường gặp những hình ảnh của đường parabol, như khi ta ngắm các đài phun nước, hoặc chiêm ngưỡng cảnh bắn pháo hoa muôn màu, muôn sắc. Nhiều công trình kiến trúc cũng được tạo dáng theo hình parabol, như cây cầu, vòm nhà, cổng ra vào,... Điều đó không chỉ bảo đảm tính bền vững mà còn tạo nên vẻ đẹp của công trình. Bài tạp Xác định toạ độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol y = X2 - 3x + 2 ; b) y - - 2x“ + 4x - 3 ; c) y = X2 - 2x ; d) y = - X2 + 4. Lập bảng biến thiên và vẽ đồ thị của các hàm số y - 3x2 - 4x + 1 ; b) y = -3x2 + 2x - 1 ; c) y = 4x2 - 4x + 1 ; d) y = -X'2 + 4x - 4 ; e) y - 2x2 + X + 1 ; f) y = -X2 + X - 1. Xác định parabol y = ax + bx + 2, biết rằng parabol đó Đi qua hai điểm M(ỉ ; 5) và 2V(- 2 ; 8) ; 3 Đi qua điểm A(3 ; - 4) và có trục đối xứng là X = ; Có đỉnh là 1(2 ; -2) ; Đi qua điểm B(-l ; 6) và tung độ của đỉnh là “. Xác định a, b, c biết parabol y - ax2 + bx + c đi qua điểm Â(8 ; 0) và có đỉnh là /(6 ; -12).

Các bài học tiếp theo

• Ôn tập chương II
• Bài 1. Đại cương về phương trình
• Bài 2. Phương trình quy về phương trình bậc nhất, bậc hai
• Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn
• Ôn tập chương III
• Bài 1. Bất đẳng thức
• Bài 2. Bất phương trình và hệ bất phương trình một ẩn
• Bài 3. Dấu của nhị thức bậc nhất
• Bài 4. Bất phương trình bậc nhất hai ẩn
• Bài 5. Dấu của tam thức bậc hai

Các bài học trước

• Bài 2. Hàm số y = ax + b
• Bài 1. Hàm số
• Ôn tập chương I
• Bài 5. Số gần đúng, sai số
• Bài 4. Các tập hợp số
• Bài 3. Các phép toán tập hợp
• Bài 2. Tập hợp
• Bài 1. Mệnh đề

Tham Khảo Thêm

• Giải Bài Tập Toán 10 Đại Số
• Giải Bài Tập Toán 10 Hình Học
• Giải Toán 10 Đại Số
• Giải Toán 10 Hình Học
• Giải Bài Tập Hình Học 10
• Sách Giáo Khoa - Đại Số 10(Đang xem)
• Sách Giáo Khoa - Hình Học 10

Sách Giáo Khoa - Đại Số 10

• Chương I. MỆNH ĐỀ, TẬP HỢP
• Bài 1. Mệnh đề
• Bài 2. Tập hợp
• Bài 3. Các phép toán tập hợp
• Bài 4. Các tập hợp số
• Bài 5. Số gần đúng, sai số
• Ôn tập chương I
• Chương II. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
• Bài 1. Hàm số
• Bài 2. Hàm số y = ax + b
• Bài 3. Hàm số bậc hai(Đang xem)
• Ôn tập chương II
• Chương III. PHƯƠNG TRÌNH - HỆ PHƯƠNG TRÌNH
• Bài 1. Đại cương về phương trình
• Bài 2. Phương trình quy về phương trình bậc nhất, bậc hai
• Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn
• Ôn tập chương III
• Chương IV. BẤT ĐẲNG THỨC - BẤT PHƯƠNG TRÌNH
• Bài 1. Bất đẳng thức
• Bài 2. Bất phương trình và hệ bất phương trình một ẩn
• Bài 3. Dấu của nhị thức bậc nhất
• Bài 4. Bất phương trình bậc nhất hai ẩn
• Bài 5. Dấu của tam thức bậc hai
• Ôn tập chương IV
• Chương V. THỐNG KÊ
• Bài 1. Bảng phân bố tần số và tần suất
• Bài 2. Biểu đồ
• Bài 3. Số trung bình cộng, số trung vị, mốt
• Bài 4. Phương sai và độ lệch chuẩn
• Ôn tập chương V
• Chương VI. CUNG VÀ GÓC LƯỢNG GIÁC - CÔNG THỨC LƯỢNG GIÁC
• Bài 1. Cung và góc lượng giác
• Bài 2. Giá trị lượng giác của một cung
• Bài 3. Công thức lượng giác
• Ôn tập chương VI
• Ôn tập cuối năm