Sin3x Cos3x Công Thức Lượng Giác - TopLoigiai
Có thể bạn quan tâm
Câu trả lời chính xác nhất:
Công thức: sin3x = 3sinx - 4sin3x
Chứng minh
sin3x = sin(2x + x)
= sin2x.cosx + cos2x.sinx
= 2sinx.cosx.cosx + (2cos2 – 1).sinx
= 2sinx.cos2x + 2cos2x.sinx – sinx
= 4sinx.cos2x – sinx
= 4sinx.(1 – sin2x) – sinx2
= 3sinx – 4sin3x
=> Điều phải chứng minh.
Công thức: Cos 3x = 4 cos2x – 3 cosx
Chứng minh
Cos3x = cos(2x + x)
= cos2x.cosx – sin2x.sinx
= (2cos2x – 1).cosx – 2sinx.cosx.sinx
= 2cos3x – cosx – 2sin2x.cosx
= 2cosx.(cos2x – sin2x) – cosx
= 2cosx.(cos2x – 1 + cos2x) – cosx
= 2cosx.(2cos2x – 1) – cosx
= 4cos3x – 2cosx – cosx
= 4cos3x – 3cosx
=> Điều phải chứng minh.
>>> Xem thêm: Sin 4x cos 4x công thức lượng giác
Để hiểu rõ hơn về công thức lượng giác, mời các bạn đến với phần nội dung dưới đây nhé.
1. Công thức lượng giác cơ bản
2. Các cung có liên quan đặc biệt
a. Cung đối nhau:
b. Cung bù nhau: x và π-x
c. Cung phụ nhau: x và π⁄2 – x
d. Cung hơn kém nhau π : χ và π + χ
e. Cung hơn kém nhau π⁄2 : χ và χ + π⁄2
3. Công thức cộng
cos (a - b) =cosacosb+sinasinb
cos (a + b) = cosacos b- sinasinb
sin (a+b) = sinacos b+ sinbcosa
sin (a-b) = sinacos b- sinbcosa
tan (a+b) =
tan (a+b) =
4. Công thức nhân đôi
sin 2a = 2 sina.cosa
cos 2a = cos2a – sin2a = 2cos2a – 1 = 1- 2sin2a
tan 2a =
cot 2a =
5. Công thức nhân ba
Sin 3x = 3 sinx – 4 sin3x
Cos 3x = 4 cos2x – 3 cosx
6. Công thức hạ bậc
Cos2x = (1 + cos2x)/2
Sin2x = (1 - cos2x)/2
Tan2x = (1 - cos2x)/(1 + cos2x)
7. Công thức tính sin x, cos x, tan x theo t = tan x/2
Sin x = 2t/(1 + t2)
Cos x = (1 - t2)/(1 + t2)
Tan x = 2t/(1 - t2)
8. Công thức biến đổi tổng thành tích
9. Công thức biến đổi tích thành tổng
10. Một số bài tập vận dụng
Bài 1: Tính: cos 225°,sin 240°, cot(-15°), tan 75°
Lời giải
Ta có: 225o = 180o + 45o
Nên cos 225o = cos (180o + 45o) = - cos 45o =
Có 240o = 180o + 60o
Nên sin 240o = sin (180o + 60o) = -sin60o =
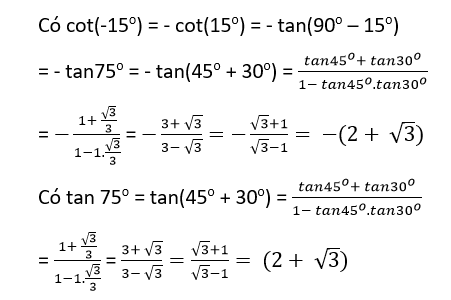
Bài 2: Chứng minh:
Ta có:
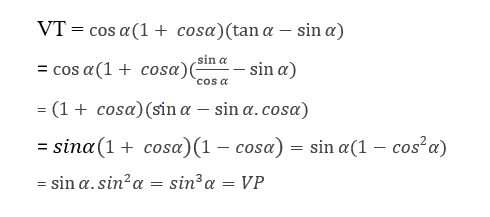

Trên đây Top lời giải đã cùng các bạn tìm hiểu về công thức lượng giác. Chúng tôi hi vọng các bạn đã có kiến thức hữu ích khi đọc bài viết này, chúc các bạn học tốt.
Từ khóa » Công Thức Sin Mũ 3 X
-
Các Công Thức Lượng Giác Toán 10 Đầy Đủ Nhất - Kiến Guru
-
Sin3x = ? - Công Thức Lượng Giác
-
Tìm Nguyên Hàm (sin(x))^3 | Mathway
-
Khai Triển Sin(3x) | Mathway
-
Làm Thế Nào để Tính đạo Hàm Của $\sin^3 X$? - Banhoituidap
-
Nguyên Hàm Sin^3(x) Integral Sin^3(x) Dx - YouTube
-
BÀI GIẢNG 5. SỬ DỤNG CÔNG THỨC HẠ BẬC CAO Biên Soạn
-
Bảng Công Thức Lượng Giác đầy đủ,chi Tiết,dễ Hiểu - DeThiThu.Net
-
Hãy Khai Triển Biểu Thức Sin(3x)
-
Tính Giá Trị Của Biểu Thức \(A=sin^3x+cos^3x\) - Nguyễn Tiểu Ly
-
Cho Tui Hỏi Tí, Có Công Thức Hạ Bậc Của Sin³x Hay Sin Mũ Bốn X Hay ...
-
Giải (sin(3x)cos(x)+sin(x)cos(3x))(sin(2x)cos ... - Microsoft Math Solver
-
Công Thức Hạ Bậc Lượng Giác