Sơ đồ Tư Duy Toán 9 Chương 1 Đại Số Cực Hay - TopLoigiai
Có thể bạn quan tâm
Căn bậc 2 và căn bậc 3 là bài đầu tiên trong chương trình đại số toán lớp 9, đây là nội dung quan trọng vì các dạng toán về căn bậc hai và căn bậc ba thường xuất hiện trong các đề thi tuyển sinh vào lớp 10. Để giải các dạng bài tập về căn bậc 2, căn bậc 3 thì các em cần nắm vững phần nội dung lý thuyết cùng các dạng bài tập về căn bậc 2 và bậc 3. Bài viết dưới đây sẽ hệ thống lại lý thuyết bằng Sơ đồ tư duy Toán 9 chương 1 Đại số và các dạng toán về căn bậc 2 và căn bậc 3 thường gặp trong Chương 1 Toán 9 Đại số để các em có thể nắm vững nội dung này.
Mục lục nội dung I. SƠ ĐỒ TƯ DUY TOÁN 9 CHƯƠNG 1Căn bậc 2Căn bậc 3II. CÁC DẠNG TOÁN VỀ CĂN BẬC 2 CĂN BẬC 3I. SƠ ĐỒ TƯ DUY TOÁN 9 CHƯƠNG 1
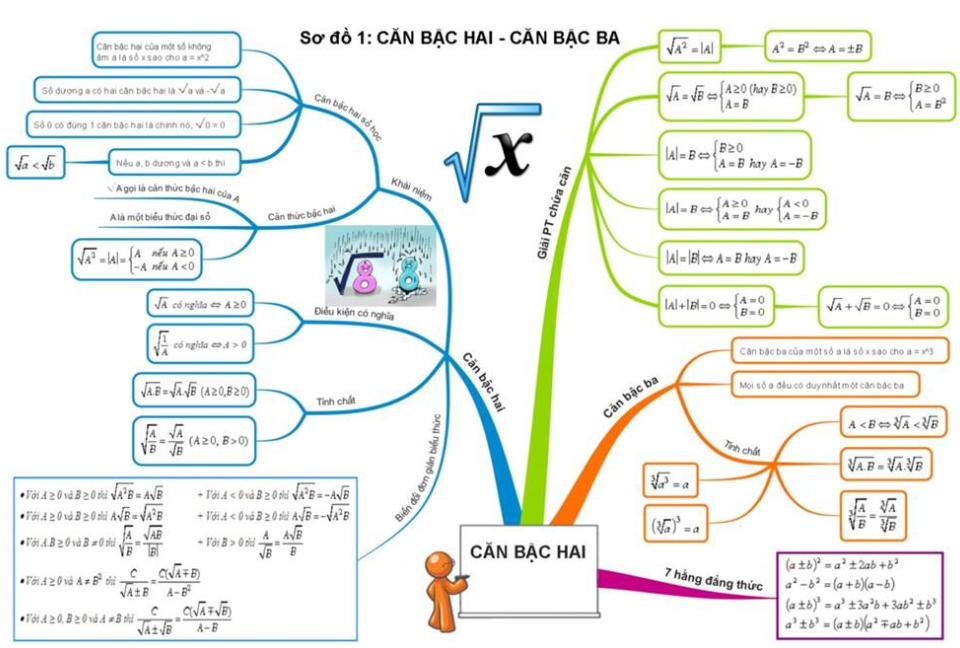

Căn bậc 2
1. Căn bậc 2 là gì?

3. Các phép biến đổi căn thức bậc 2 cơ bản
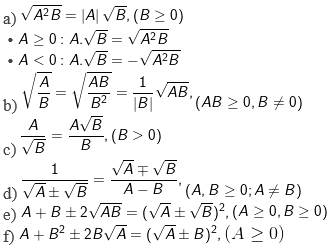
Căn bậc 3
1. Căn bậc là gì?
- Định nghĩa: Căn bậc ba của một số a là số x sao cho x3 = a.
2. Tính chất của căn bậc 3
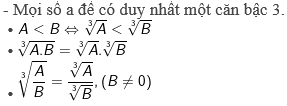
II. CÁC DẠNG TOÁN VỀ CĂN BẬC 2 CĂN BẬC 3

• Dạng 2: Rút gọn biểu thức chứa căn thức
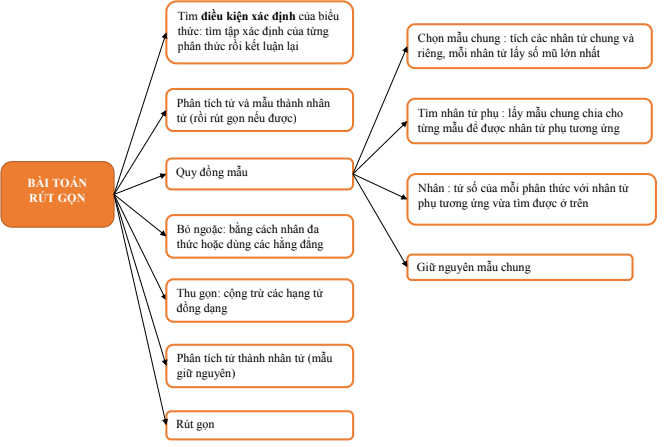
- Để rút gọn các biểu thức chứa căn cần vận dụng thích hợp các phép toán đơn giản như: đưa thừa số ra ngoài dấu căn, vào trong dấu căn, trục căn thức ở mẫu, sử dụng hằng đẳng thức để phân tích thành nhân tử và tìm mẫu thức chung ...
- Nếu bài toán chưa cho điều kiện của xx thì ta cần phải tìm điều kiện trước khi rút gọn.
- Trong các đề thi Toán vào 10, sau khi rút gọn biểu thức, ta thường gặp các bài toán liên quan như:
+) Tính giá trị của A tại x=x0
+) Tìm x để A > m; A < m hay A = m.
+) Tìm GTLN hoặc GTNN của A.
+) Tìm x nguyên để A nguyên.
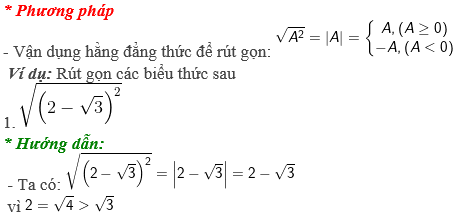
• Dạng 3: Thực hiện phép tính rút gọn biểu thức
* Phương pháp
- Vận dụng các phép biến đổi và đặt nhân tử chung
Ví dụ: Rút gọn các biểu thức sau
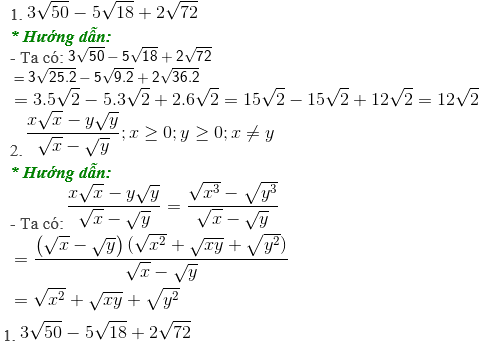
• Dạng 4: Giải phương trình có chứa căn thức

• Dạng 5: Chứng minh các đẳng thức
* Phương pháp:
- Thực hiện các phép biến đổi đẳng thức chứa căn bậc 2
- Vận dụng phương pháp chứng minh đẳng thức A = B
+ Chứng minh A = C và B = C
+ Biến đổi A về B hoặc B về A (tức A = B)
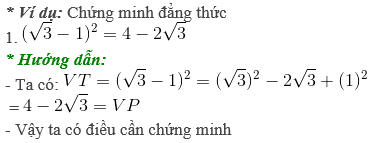
Vậy là các em đã hoàn thành chuyên đề Sơ đồ tư duy Toán 9 chương 1 đại số, Top lời giải hi vọng các em đã nắm chắc lý thuyết và vận dụng vào các bài tập liên quan đến căn bậc hai, căn bậc 3. Cùng theo dõi Top lời giải và xem thêm các chuyên đề hay ở trong chuyên mục này nhé. Hãy đặt câu hỏi giúp phần comment để đội ngũ thầy cô giáo của Top lời giải hỗ trợ tốt hơn cho bạn.
Từ khóa » Sơ đồ Tư Duy Toán 9 Chương 1 đại Số
-
Sơ đồ Tư Duy Toán 9 Chương 1 đại Số
-
Sơ đồ Tư Duy đại Số 9 Chương 1 - Căn Bậc Ba - YouTube
-
Sơ đồ Tư Duy Toán 9 Chương 1 đại Số
-
Sơ đồ Tư Duy Toán 9 Chương 1 đại Số
-
Trọn Bộ Sơ đồ Tư Duy Toán 9 Chương 1 đại Số (UPDATE 2022)
-
Chinh Phục Toán 9 Bằng Sơ đồ Tư Duy Tập 1
-
Sơ đồ Tư Duy Toán 9 đại Số Chương 1 - 123doc
-
Sơ đồ Tư Duy Môn Toán 9 Chương 1 - 123doc
-
I. Sơ đồ Tư Duy Toán 9 Chương 1
-
Sơ đồ Tư Duy Toán 9 Chương 1 Hình Học Cực Hay - MarvelVietnam
-
Sơ đồ Tư Duy Môn Toán 9 Chương 1 Hình Học - 123doc - MarvelVietnam
-
Sơ đồ Tư Duy Toán Lớp 9
-
Sơ đồ Tư Duy Toán 9 Chương 1 Hình Học - Trần Gia Hưng