Số Giao điểm Của đồ Thị Hàm Số (y = (x^4) - 5(x^2) + 4 ) Với Trụ

Một sản phẩm của Tuyensinh247.comSố giao điểm của đồ thị hàm số (y = (x^4) - 5(x^2) + 4 ) với trục hoành làCâu 62636 Thông hiểu

Số giao điểm của đồ thị hàm số \(y = {x^4} - 5{x^2} + 4\) với trục hoành là

Đáp án đúng: cÔn thi đánh giá năng lực 2024 - lộ trình 5v bài bảnkhám phá

Phương pháp giải

Giải phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành. Số nghiệm của phương trình chính là số giao điểm.

Xem lời giải

Lời giải của GV Vungoi.vn

Xét phương trình hoành độ giao điểm: \({x^4} - 5{x^2} + 4 = 0 \Leftrightarrow \left( {{x^2} - 4} \right)\left( {{x^2} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \pm 2\\x = \pm 1\end{array} \right.\) .

Vậy số giao điểm của đồ thị hàm số đã cho với trục hoành là 4.

Đáp án cần chọn là: c

DÀNH CHO 2K6 – LỘ TRÌNH ÔN THI ĐÁNH GIÁ NĂNG LỰC 2024!

Bạn đăng băn khoăn tìm hiểu tham gia thi chưa biết hỏi ai?

Bạn cần lộ trình ôn thi bài bản từ những người am hiểu về kì thi và đề thi?

Bạn cần thầy cô đồng hành suốt quá trình ôn luyện?

Vậy thì hãy xem ngay lộ trình ôn thi bài bản tại ON.TUYENSINH247:

• Hệ thống kiến thức trọng tâm & làm quen các dạng bài chỉ có trong kỳ thi ĐGNL
• Phủ kín lượng kiến thức với hệ thống ngân hàng hơn 15.000 câu hỏi độc quyền
• Học live tương tác với thầy cô kết hợp tài khoản tự luyện chủ động trên trang

Xem thêm thông tin khoá học & Nhận tư vấn miễn phí - TẠI ĐÂY

...

Bài tập có liên quan

Khảo sát sự biến thiên và vẽ đồ thị hàm số (tương giao đồ thị) Luyện Ngay

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi liên quan

Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:

Số giao điểm của đồ thị hàm số $y = {x^3} - 2{x^2} + x - 1$ và đường thẳng $y = 1 - 2x$ là:

Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?

Các đồ thị hàm số $y = {x^4} - 2{x^2} + 2$ và $y = - {x^2} + 4$ có tất cả bao nhiêu điểm chung?

Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:

Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.

Cho hàm số $y = {x^3} + 3{x^2} + m$ có đồ thị $\left( C \right)$.Để đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A,B,C$ sao cho $C$ là trung điểm của $AB$ thì giá trị của tham số $m$ là:

Biết đường thẳng $y = mx + 1$ cắt đồ thị hàm số $y = {x^3} - 3x + 1$ tại ba điểm phân biệt. Tất cả các giá trị thực của tham số $m$ là:

Cho hàm số $y = {x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right)$. Tập hợp tất cả các giá trị của $m$ để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:

Tìm $m$ để đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ cắt đường thẳng $y = m\left( {x - 1} \right)$ tại ba điểm phân biệt có hoành độ ${x_1},{x_2},{x_3}$ thỏa mãn $x_1^2 + x_2^2 + x_3^2 = 5$.

Tìm điều kiện của $m$ để đồ thị hàm số $\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1$ cắt trục hoành tại $4$ điểm phân biệt.

Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$

Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

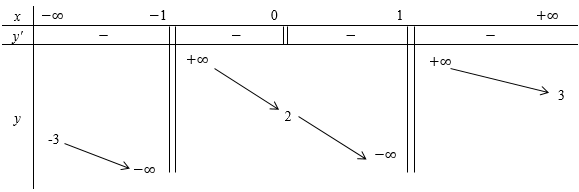
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.

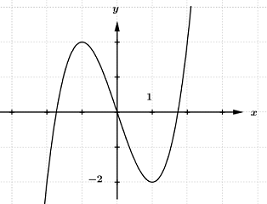
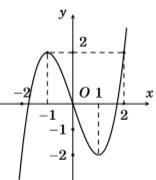
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là:

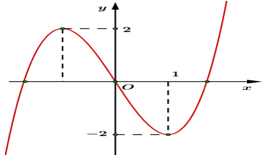
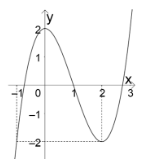
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:

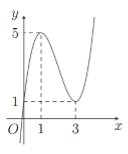
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + 4m + 4} \right)\) có nghiệm?

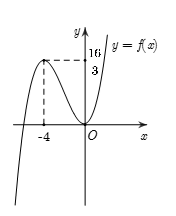
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau

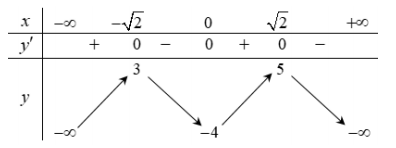
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( {\sin x - \cos x} \right) = m - 1\) có hai nghiệmphân biệt trên khoảng \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)?\)

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.

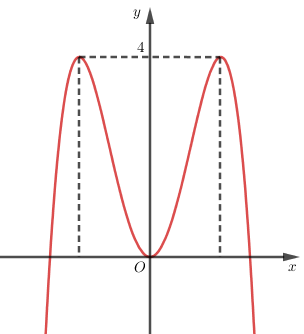
Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên trong hình dưới:

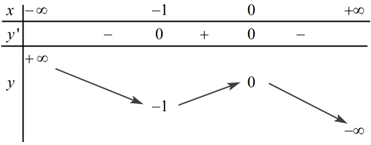
Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ

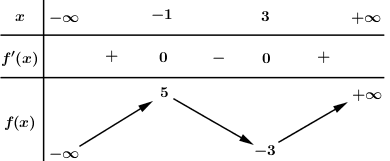
Phương trình \(\left| {f\left( {3x + 1} \right) - 2} \right| = 5\) có bao nhiêu nghiệm?

Có tất cả bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 2020;2020} \right]\) của tham số m để đường thẳng \(y = x + m\) cắt đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x - 1}}\) tại hai điểm phân biệt?

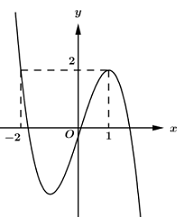
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( {1 - f\left( x \right)} \right) = 2\) là:

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:

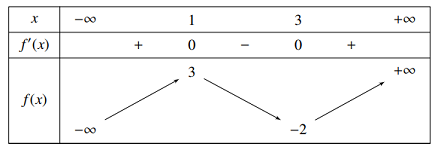
Tìm tất cả các giá trị của \(m\) để bất phương trình \(f\left( {3 - {x^2}} \right) \ge m\) vô nghiệm?

Cho hàm số \(y = {x^3} + 2m{x^2} + \left( {m + 3} \right)x + 4\,\,\,\left( {{C_m}} \right)\). Giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = x + 4\) cắt \(\left( {{C_m}} \right)\) tại ba điểm phân biệt \(A\left( {0;4} \right),\,\,B,\,\,C\) sao cho tam giác \(KBC\) có diện tích bằng \(8\sqrt 2 \) với điểm \(K\left( {1;3} \right)\) là:

Cho hàm số $y = {x^4} - 4{x^2} + 3$. Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $\left| {{x^4} - 4{x^2} + 3} \right| = m$ có $4$ nghiệm phân biệt.

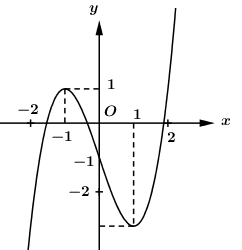
Cho \(y = f\left( x \right)\) là hàm đa thức bậc 3 và có đồ thị như hình vẽ bên. Hỏi phương trình \(f\left[ {f\left( {\cos x} \right) - 1} \right] = 0\) có bao nhiêu nghiệm thuộc đoạn \(\left[ {0;3\pi } \right]\)?

Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Tổng tất cả giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt {2f\left( {\cos x} \right)} } \right) = m\) có nghiệm \(x \in \left[ {\dfrac{\pi }{2};\pi } \right)\) là:

Cho hàm số \(y = f\left( x \right)\) là hàm số đa thức bậc bốn. Biết \(f\left( 0 \right) = 0\) và đồ thị hàm số \(y = f'\left( x \right)\) có hình vẽ bên dưới.

Tập nghiệm của phương trình \(f\left( {\left| {2\sin x - 1} \right| - 1} \right) = m\) (với \(m\) là tham số) trên đoạn \(\left[ {0;3\pi } \right]\) có tối đa bao nhiêu phần tử?

Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây

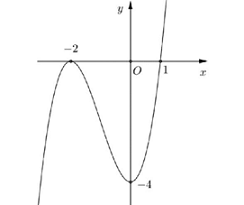
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\) nghiệm phân biệt

Có bao nhiêu giá trị nguyên của m để phương trình sau có 8 nghiệm thực phân biệt

\({\left( {{x^2} - 6\left| x \right| - 1} \right)^2} - \left( {m - 5} \right)\left| x \right|\left( {\left| x \right| - 6} \right) + 1 - m = 0\)

Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

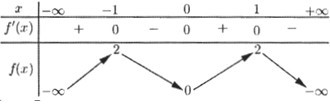
Số nghiệm thuộc đoạn \(\left[ {0;\dfrac{{5\pi }}{2}} \right]\) của phương trình \(f\left( {\sin \,x} \right) = 1\) là:

Tìm $m \ne 0$ để phương trình ${x^2}\left| {x - 3} \right| = m + \dfrac{1}{m}$ có 4 nghiệm phân biệt.

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

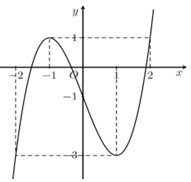
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {f\left( x \right) + m} \right) + 1 = f\left( x \right) + m\) có đúng 3 nghiệm phân biệt trên \(\left[ { - 1;1} \right]\).

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.

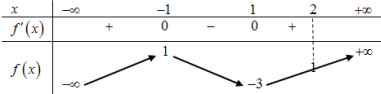
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {2f\left( x \right) + m} \right|} \right) = 1\) có đúng 2 nghiệm trên \(\left[ { - 1;1} \right]\).

Tìm $m$ để phương trình $2{\left| x \right|^3} - 9{x^2} + 12\left| x \right| = m$ có $6$ nghiệm phân biệt.

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có bảng biến thiên như hình vẽ:

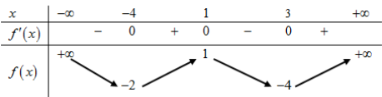
Số nghiệm của phương trình \(\left| {f\left( {f\left( x \right)} \right)} \right| = 2\) là:

Cho hàm số \(y = \dfrac{x}{{1 - x}}\,\,\left( C \right)\) và điểm \(A\left( { - 1;1} \right)\). Tìm \(m\) để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) sao cho \(A{M^2} + A{N^2}\) đạt giá trị nhỏ nhất.

Đề thi THPT QG - 2021 - mã 101

Đồ thị hàm số \(y = - {x^4} + 4{x^2} - 3\) cắt trục tung tại điểm có tung độ bằng

Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

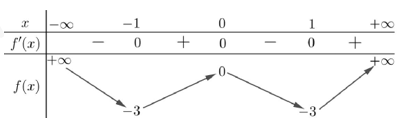
Phương trình \(f\left( {{x^2} - 1} \right) + 1 = 0\) có bao nhiêu nghiệm thực?

Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới.

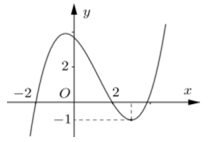
Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} - 3x} \right)} \right| = \dfrac{2}{3}\) là

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.

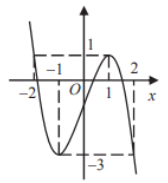
Hỏi phương trình \(f\left( {2 - f\left( x \right)} \right) = 1\) có tất cả bao nhiêu nghiệm thực phân biệt?

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( {\sqrt {4 - {x^2}} } \right) = m\) có nghiệm thuộc nửa khoảng \(\left[ { - \sqrt 2 ;\sqrt 3 } \right)\) là

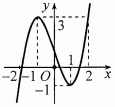
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có đúng hai nghiệm trên đoạn \(\left[ {0;\pi } \right]\).

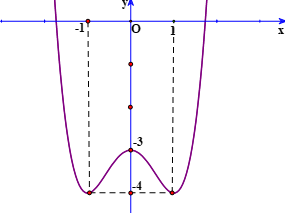
Cho hàm số \(y = {x^3} - (2m + 1){x^2} \)\(+ \left( {{m^2} - m + 3} \right)x \)\(+ 2{m^2} - 3m\)

Số giá trị nguyên của \(m\) thuộc \(( - 20;10)\) để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là