Soạn Toán 8 Bài 2 Nhân đa Thức Với đa Thức VNEN

Trang chủ » Giải Vnen Toán 8 » Soạn Toán 8 Bài 2 Nhân đa Thức Với đa Thức VNEN

Có thể bạn quan tâm

Soạn Toán 8 bài 2 Nhân đa thức với đa thức VNEN Soạn Toán 8 tập 1 phần đại số Bài trước Tải về Bài sau Lớp: Lớp 8 Môn: Toán Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

VnDoc xin giới thiệu tới các bạn bài Soạn Toán 8 VNEN bài 2 Nhân đa thức với đa thức. Tài liệu này hướng dẫn các bạn trả lời các câu hỏi trong SGK VNEN lớp 9. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học tốt môn Toán lớp 9. Mời các bạn tham khảo

Soạn Toán 8 bài 2 Nhân đa thức với đa thức

  • A. Hoạt động khởi động
    • 1. Quan sát và trả lời câu hỏi
  • B. Hoạt động hình thành kiến thức
    • 1. Thực hiện phép nhân:
  • C. Hoạt động luyện tập
    • Câu 2: Trang 9 toán VNEN 8 tập 1
    • Câu 3: Trang 9 toán VNEN 8 tập 1
    • Câu 4: Trang 9 toán VNEN 8 tập 1
    • Câu 5: Trang 9 toán VNEN 8 tập 1
  • D. E. Hoạt động vận dụng và tìm tòi, mở rộng
    • Câu 2: Trang 10 toán VNEN 8 tập 1
    • Câu 3: Trang 10 toán VNEN 8 tập 1

A. Hoạt động khởi động

1. Quan sát và trả lời câu hỏi

Xét mặt dưới của một hộp quà:

a) Hai đoạn dây buộc hộp quà chia mặt dưới thành 4 hình. Diện tích mỗi hình là bao nhiêu?

b) Em có thể tính diện tích mặt dưới hộp quà đó bằng những cách nào?

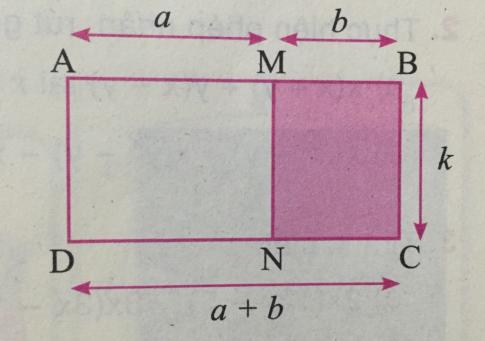
Soạn Toán 8 bài 2 Nhân đa thức với đa thức VNEN

Trả lời:

a) Diện tích mỗi hình chữ nhật được chia ra bởi hai đoạn dây buộc hộp quà là: c.a; c.b; d.a; d.b.

b) Có hai cách để tính diện tích mặt dưới hộp quà.

Cách 1: Diện tích hộp quà bằng (a + b).(c + d).

Cách 2: Diện tích hộp quà bằng c.a + c.b + d.a + d.b.

B. Hoạt động hình thành kiến thức

1. Thực hiện phép nhân:

a) (xy – 2)(xy + 5);\(a) (xy – 2)(xy + 5);\)

b) (\frac{1}{3}xy – 2)(x^{3} - 3x + 6).\(b) (\frac{1}{3}xy – 2)(x^{3} - 3x + 6).\)

Trả lời:

a) (xy – 2)(xy + 5) = x^{2}y^{2}+ 5xy – 2xy – 10 = x^{2}y^{2}+ 3xy – 10;\(a) (xy – 2)(xy + 5) = x^{2}y^{2}+ 5xy – 2xy – 10 = x^{2}y^{2}+ 3xy – 10;\)

b) (\frac{1}{3}xy – 2)(x^{3}- 3x + 6) =\frac{1}{3}x^{4}y - x^{2}y + 2xy – 2x^{3} + 6x – 12.\(b) (\frac{1}{3}xy – 2)(x^{3}- 3x + 6) =\frac{1}{3}x^{4}y - x^{2}y + 2xy – 2x^{3} + 6x – 12.\)

C. Hoạt động luyện tập

Câu 1: Trang 9 toán VNEN 8 tập 1

Thực hiện phép nhân đa thức với đa thức:

a) (x + 2x + 1)(x + 1);\(a) (x + 2x + 1)(x + 1);\)

b) (x^{3} - x^{2} + 2x – 1)(5 – x).\(b) (x^{3} - x^{2} + 2x – 1)(5 – x).\)

Từ câu b), hãy suy ra kết quả phép nhân: (x – 5)(x^{3} - x^{2} + 2x – 1)\((x – 5)(x^{3} - x^{2} + 2x – 1)\)

Bài làm:

a) (x + 2x + 1)(x + 1) = (3x + 1)(x + 1) = 3x^{2}+ 3x + x + 1 = 3x^{2}+ 4x + 1;\(a) (x + 2x + 1)(x + 1) = (3x + 1)(x + 1) = 3x^{2}+ 3x + x + 1 = 3x^{2}+ 4x + 1;\)b) (x^{3}- x^{2}+ 2x – 1)(5 – x) = -x^{4} + x^{3} - 2x^{2} + x + 5x^{3}\(b) (x^{3}- x^{2}+ 2x – 1)(5 – x) = -x^{4} + x^{3} - 2x^{2} + x + 5x^{3}\)- 5x^{2} + 10x - 5 = -x^{4} + 6x^{3} - 7x^{2} + 11x - 5.\(- 5x^{2} + 10x - 5 = -x^{4} + 6x^{3} - 7x^{2} + 11x - 5.\)\Rightarrow (x – 5)(x^{3} - x^{2} + 2x – 1) = x^{4} - 6x^{3} + 7x^{2} - 11x + 5.\(\Rightarrow (x – 5)(x^{3} - x^{2} + 2x – 1) = x^{4} - 6x^{3} + 7x^{2} - 11x + 5.\)

Câu 2: Trang 9 toán VNEN 8 tập 1

Thực hiện phép tính:

a)(x-y)(x^2+xy+y^2);\(a)(x-y)(x^2+xy+y^2);\)

b)(x^2-2xy+y^2)(x-y);\(b)(x^2-2xy+y^2)(x-y);\)c)(x^2y^2-\frac{1}{3}xy+3y)(x-3y);\(c)(x^2y^2-\frac{1}{3}xy+3y)(x-3y);\)

d)(\frac{1}{5}x-1)(x^2-5x+2).\(d)(\frac{1}{5}x-1)(x^2-5x+2).\)

Bài làm:

a) (x – y)(x^{2}+ xy + y^{2}) = x^{3}+ x^{2}y + xy^{2} - x^{2}y - xy^{2} - y^{3} = x^{3} - y^{3};\(a) (x – y)(x^{2}+ xy + y^{2}) = x^{3}+ x^{2}y + xy^{2} - x^{2}y - xy^{2} - y^{3} = x^{3} - y^{3};\)b) (x^{2}- 2xy + y^{2})(x – y) = x^{3}- 2x^{2}y + xy^{2} - x^{2}y\(b) (x^{2}- 2xy + y^{2})(x – y) = x^{3}- 2x^{2}y + xy^{2} - x^{2}y\) + 2xy^{2} - y^{3} = x^{3} - 3x^{2}y + 3xy^{2} - y^{3};\(+ 2xy^{2} - y^{3} = x^{3} - 3x^{2}y + 3xy^{2} - y^{3};\)c) (x^{2}y^{2}-\frac{1}{3}xy + 3y)(x – 3y) = x^{3}y^{2}\(c) (x^{2}y^{2}-\frac{1}{3}xy + 3y)(x – 3y) = x^{3}y^{2}\)- \frac{1}{3}x^{2}y + 3xy – 3x^{2}y^{3} + xy^{2} - 9y^{2};\(- \frac{1}{3}x^{2}y + 3xy – 3x^{2}y^{3} + xy^{2} - 9y^{2};\)d) (\frac{1}{5}x – 1)(x^{2}- 5x + 2) =\frac{1}{5}x^{3} - x^{2} + \frac{2}{5}x - x^{2} + 5x – 2 = \frac{1}{5}x^{3} - 2x^{2} + \frac{27}{5}x - 2.\(d) (\frac{1}{5}x – 1)(x^{2}- 5x + 2) =\frac{1}{5}x^{3} - x^{2} + \frac{2}{5}x - x^{2} + 5x – 2 = \frac{1}{5}x^{3} - 2x^{2} + \frac{27}{5}x - 2.\)

Câu 3: Trang 9 toán VNEN 8 tập 1

Điền kết quả tính được vào ô trống trong bảng:

Giá trị của x và y Giá trị của biểu thức (x + y)(x^{2} - xy + y^{2})\((x + y)(x^{2} - xy + y^{2})\)
x = -10; y = 1
x = -1; y = 0
x = 2; y = -1
x = -0,5 y = 1,25

Bài làm:

Giá trị của x và y

 Giá trị của biểu thức (x + y)(x^{2} - xy + y^{2})\((x + y)(x^{2} - xy + y^{2})\)
x = -10; y = 1 81
x = -1; y = 0 -1
x = 2; y = -1 7
x = -0,5 y = 1,25 1,828125

Câu 4: Trang 9 toán VNEN 8 tập 1

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:

(x – 5)(3x + 3) – 3x(x – 3) + 3x + 7.\((x – 5)(3x + 3) – 3x(x – 3) + 3x + 7.\)

Bài làm:

Có: (x – 5)(3x + 3) – 3x(x – 3) + 3x + 7 = 3x^{2} + 3x – 15x – 15 – 3x^{2} + 9x + 3x + 7 = -8.\((x – 5)(3x + 3) – 3x(x – 3) + 3x + 7 = 3x^{2} + 3x – 15x – 15 – 3x^{2} + 9x + 3x + 7 = -8.\)

Vậy giá trị của biểu thức trên luôn bằng -8 và không phụ thuộc vào giá trị của biến.

Câu 5: Trang 9 toán VNEN 8 tập 1

Tìm x, biết: (x + 2)(x + 1) – (x – 3)(x + 5) = 0.\((x + 2)(x + 1) – (x – 3)(x + 5) = 0.\)

Bài làm:

(x + 2)(x + 1) – (x – 3)(x + 5) = 0\((x + 2)(x + 1) – (x – 3)(x + 5) = 0\)

\Leftrightarrow x^{2} + x + 2x + 2 – (x^{2} + 5x – 3x – 15) = 0\(\Leftrightarrow x^{2} + x + 2x + 2 – (x^{2} + 5x – 3x – 15) = 0\)

\Leftrightarrow x^{2} + 3x + 2 - x^{2} - 2x + 15 = 0\(\Leftrightarrow x^{2} + 3x + 2 - x^{2} - 2x + 15 = 0\)

\Leftrightarrow x + 17 = 0\(\Leftrightarrow x + 17 = 0\)

\Leftrightarrow x = -17.\(\Leftrightarrow x = -17.\)

D. E. Hoạt động vận dụng và tìm tòi, mở rộng

Câu 2: Trang 10 toán VNEN 8 tập 1

Tìm ba số tự nhiên chẵn liên tiếp biết tích của hai số sau lớn hơn tích của hai số đầu là 192.

Bài làm:

Gọi 3 số chẵn liên tiếp cần tìm là a; a + 2 và a + 4.

Theo đề bài, ta có:

(a + 2)(a + 4) – a(a + 2) = 192\((a + 2)(a + 4) – a(a + 2) = 192\)

\Leftrightarrow a^{2} + 4a + 2a + 8 - a^{2} - 2a = 192\(\Leftrightarrow a^{2} + 4a + 2a + 8 - a^{2} - 2a = 192\)

\Leftrightarrow 4a + 8 = 192\(\Leftrightarrow 4a + 8 = 192\)

\Leftrightarrow 4a = 192 – 8\(\Leftrightarrow 4a = 192 – 8\)

\Leftrightarrow 4a = 184\(\Leftrightarrow 4a = 184\)

\Leftrightarrow a = 184 : 4\(\Leftrightarrow a = 184 : 4\)

\Leftrightarrow a = 46\(\Leftrightarrow a = 46\)

Vậy 3 chẵn cần tìm là 46; 48; 50.

Câu 3: Trang 10 toán VNEN 8 tập 1

Chứng minh rằng giá trị của biểu thức n(n + 5) – (n – 3)(n + 2)\(n(n + 5) – (n – 3)(n + 2)\) luôn chia hết cho 6 với mọi n là số nguyên.

Bài làm:

Ta có: n(n + 5) – (n – 3)(n + 2) = n^{2} + 5n – (n^{2} - 3n + 2n – 6)\(n(n + 5) – (n – 3)(n + 2) = n^{2} + 5n – (n^{2} - 3n + 2n – 6)\)

= n^{2} + 5n – n^{2} + 3n – 2n + 6)\(= n^{2} + 5n – n^{2} + 3n – 2n + 6)\)

= 6n + 6 = 6(n + 1) \vdots 6\(= 6n + 6 = 6(n + 1) \vdots 6\) với mọi n là số nguyên

Vậy giá trị của biểu thức n(n + 5) – (n – 3)(n + 2)\(n(n + 5) – (n – 3)(n + 2)\) luôn chia hết cho 6 với mọi n là số nguyên.

Soạn Toán 8 bài 2 Nhân đa thức với đa thức VNEN. Trên đây VnDoc đã hướng dẫn các bạn soạn Toán 8, lời giải chi tiết dễ hiểu hy vọng sẽ giúp các bạn củng cố thêm kiến thức từ đó vận dụng vào giải các các bài tập Toán lớp 8. Mời các bạn cùng tham khảo

.............................................

Ngoài Soạn Toán 8 bài 2 Nhân đa thức với đa thức VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 8, Giải Vở BT Toán 8 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Từ khóa » Giải Vnen Toán 8