Soạn Toán 9 Bài 2 Luyện Tập VNEN

Trang chủ » Học Vnen Toán 9 » Soạn Toán 9 Bài 2 Luyện Tập VNEN

Có thể bạn quan tâm

      • Mầm non

      • Lớp 1

      • Lớp 2

      • Lớp 3

      • Lớp 4

      • Lớp 5

      • Lớp 6

      • Lớp 7

      • Lớp 8

      • Lớp 9

      • Lớp 10

      • Lớp 11

      • Lớp 12

      • Thi vào lớp 6

      • Thi vào lớp 10

      • Thi Tốt Nghiệp THPT

      • Đánh Giá Năng Lực

      • Khóa Học Trực Tuyến

      • Hỏi bài

      • Trắc nghiệm Online

      • Tiếng Anh

      • Thư viện Học liệu

      • Bài tập Cuối tuần

      • Bài tập Hàng ngày

      • Thư viện Đề thi

      • Giáo án - Bài giảng

      • Tất cả danh mục

    • Mầm non
    • Lớp 1
    • Lớp 2
    • Lớp 3
    • Lớp 4
    • Lớp 5
    • Lớp 6
    • Lớp 7
    • Lớp 8
    • Lớp 9
    • Lớp 10
    • Lớp 11
    • Lớp 12
    • Thi Chuyển Cấp
Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 9 Soạn Toán 9 VNEN Soạn Toán 9 bài 2 Luyện tập VNEN Soạn Toán 9 tập 1 phần hình học Bài trước Bài sau Lớp: Lớp 9 Môn: Toán Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Bài 2 Luyện tập VNEN

Soạn Toán 9 VNEN bài 2 Luyện tập được VnDoc sưu tầm và đăng tải. Đây là lời giải hay cho các câu hỏi trong Sách SGK nằm trong chương trình giảng dạy môn Toán lớp 9. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các bạn học sinh. Mời thầy cô cùng các bạn học sinh tham khảo

C. Hoạt động luyện tập

Câu 1: Trang 63 sách VNEN 9 tập 1

Tính x, y trong mỗi hình sau:

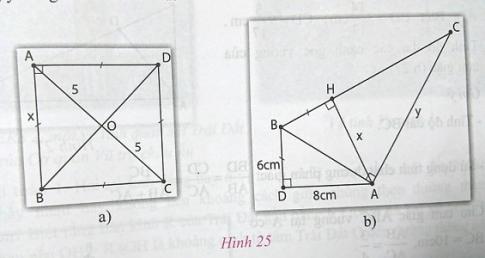
Soạn Toán 9 bài 2 Luyện tập VNEN

Bài làm:

* Hình 25a

Ta có tứ giác ABCD là hình thoi có góc A vuông nên ABCD là hình vuông

Áp dụng công thức b^{2} = ab\(b^{2} = ab'\)cho tam giác vuông ABC, ta có:

x^{2} = 5.(5 + 5)\(x^{2} = 5.(5 + 5)\)

\Rightarrow x = 5\sqrt{2}\(\Rightarrow x = 5\sqrt{2}\)

* Hình 25b

Ta có: \Delta ABD = \Delta ABH\(\Delta ABD = \Delta ABH\) (cạnh huyền - cạnh góc vuông)

\Rightarrow x = 8cm\(\Rightarrow x = 8cm\)

Áp dụng định lý Py-ta-go ta có: AB = \sqrt{6^{2} + 8^{2}} = 10 cm\(AB = \sqrt{6^{2} + 8^{2}} = 10 cm\)

Áp dụng công thức \frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}\(\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}\) ta có:

\frac{1}{x^{2}} = \frac{1}{AB^{2}} + \frac{1}{y^{2}} \Leftrightarrow \frac{1}{8^{2}} = \frac{1}{10^{2}} + \frac{1}{y^{2}}\(\frac{1}{x^{2}} = \frac{1}{AB^{2}} + \frac{1}{y^{2}} \Leftrightarrow \frac{1}{8^{2}} = \frac{1}{10^{2}} + \frac{1}{y^{2}}\)

\Rightarrow y = \frac{40}{3} cm.\(\Rightarrow y = \frac{40}{3} cm.\)

Câu 2: Trang 64 sách VNEN 9 tập 1

Cho tam giác vuông với các cạnh góc vuông có độ dài là 3cm và 4cm. Kẻ đường cao ứng với cạnh huyền. Tính độ dài các đoạn thẳng mà nó chia ra trên cạnh huyền và diện tích các tam giác vuông tạo thành.

Gợi ý (h.26):

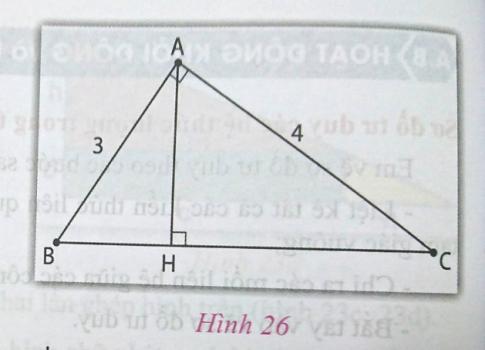
Soạn Toán 9 bài 2 Luyện tập VNEN

- Tính độ dài BC.

- Tính BH, CH theo công thức b^{2} = ab\(b^{2} = ab', c^{2} = ac'\).

- Tính diện tích theo công thức: S = \frac{1}{2}AB.AC\(S = \frac{1}{2}AB.AC\)

Bài làm:

* Áp dụng định lý Py-ta-go ta có:

BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{3^{2} + 4^{2}} = 5\(BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{3^{2} + 4^{2}} = 5\)

* Áp dụng công thức b^{2} = ab\(b^{2} = ab'\), ta có:

AB^{2} = BH.BC \Rightarrow BH = \frac{AB^{2}}{BC} = 1,8\(AB^{2} = BH.BC \Rightarrow BH = \frac{AB^{2}}{BC} = 1,8\)

AC^{2} = CH.BC \Rightarrow CH = \frac{AC^{2}}{BC} = 3,2.\(AC^{2} = CH.BC \Rightarrow CH = \frac{AC^{2}}{BC} = 3,2.\)

Áp dụng công thức h^{2} = b\(h^{2} = b'.c'\), ta có:

AH^{2} = BH.CH \Rightarrow AH = 2,4\(AH^{2} = BH.CH \Rightarrow AH = 2,4\)

* Diện tích tam giác vuông ABC là:

S\Delta ABC = \frac{1}{2}AB.AC = \frac{1}{2}.3.4 = 6\(S\Delta ABC = \frac{1}{2}AB.AC = \frac{1}{2}.3.4 = 6\)

* Diện tích tam giác vuông ABH là:

S\Delta ABH = \frac{1}{2}AH.BH = \frac{1}{2}.2,4.1,8 = 2,16\(S\Delta ABH = \frac{1}{2}AH.BH = \frac{1}{2}.2,4.1,8 = 2,16\)

* Diện tích tam giác vuông ACH là:

S\Delta ACH = \frac{1}{2}AH.CH = \frac{1}{2}.2,4.3,2 = 3,84.\(S\Delta ACH = \frac{1}{2}AH.CH = \frac{1}{2}.2,4.3,2 = 3,84.\)

Câu 3: Trang 64 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại A, phân giác AD. Biết BD = 3\frac{14}{17} cm\(BD = 3\frac{14}{17} cm\); CD = 9\frac{3}{17} cm\(CD = 9\frac{3}{17} cm\). Tính độ dài các cạnh góc vuông của tam giác (h.27).

Gợi ý:

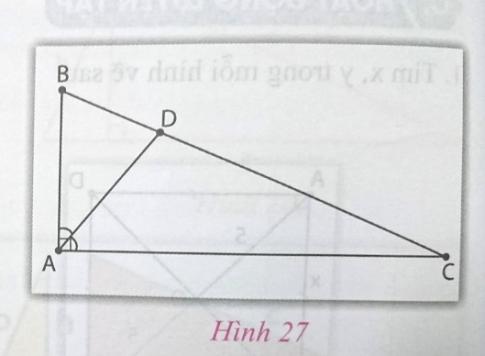
Soạn Toán 9 bài 2 Luyện tập VNEN

- Tính độ dài BC.

- Sử dụng tính chất đường phân giác: \frac{BD}{AB} = \frac{CD}{AC} = \frac{BC}{AB + AC}\(\frac{BD}{AB} = \frac{CD}{AC} = \frac{BC}{AB + AC}\).

Bài làm:

Ta có BC = BD + CD = 3\frac{14}{17} + 9\frac{3}{17} = 13 cm\(BC = BD + CD = 3\frac{14}{17} + 9\frac{3}{17} = 13 cm\)

Theo tính chất đường phân giác ta có:

\frac{BD}{AB} = \frac{CD}{AC} = \frac{BC}{AB + AC}\(\frac{BD}{AB} = \frac{CD}{AC} = \frac{BC}{AB + AC}\)

Xét: \frac{BD}{AB} = \frac{CD}{AC} \Leftrightarrow BD.AC = CD.AB \Leftrightarrow 3\frac{14}{17}.AC = 9\frac{3}{17}.AB \Leftrightarrow AC = 2,4AB\(\frac{BD}{AB} = \frac{CD}{AC} \Leftrightarrow BD.AC = CD.AB \Leftrightarrow 3\frac{14}{17}.AC = 9\frac{3}{17}.AB \Leftrightarrow AC = 2,4AB\)

Mặt khác tam giác ABC là tam giác vuông nên:

AB^{2} + AC^{2} = BC^{2} \Leftrightarrow AB^{2} + (2,4AB)^{2} = 13^{2} \Leftrightarrow 6,76AB^{2} = 169 \Leftrightarrow AB = 5 cm\(AB^{2} + AC^{2} = BC^{2} \Leftrightarrow AB^{2} + (2,4AB)^{2} = 13^{2} \Leftrightarrow 6,76AB^{2} = 169 \Leftrightarrow AB = 5 cm\)

Suy ra AC = 12cm.

Câu 4: Trang 64 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại A có BC = 10cm, \frac{AB}{AC} = \frac{3}{4}\(BC = 10cm, \frac{AB}{AC} = \frac{3}{4}\)

a) Tính độ dài các cạnh AB, AC.

b) Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính độ dài đoạn thẳng MN, MC

Hướng dẫn (h.28)

Soạn Toán 9 bài 2 Luyện tập VNEN

b) + Sử dụng tính chất đường phân giác \frac{AM}{BA} = \frac{MC}{BC}\(\frac{AM}{BA} = \frac{MC}{BC}\) để tính MA, MC.

+ Chú ý rằng hai đường phân giác trong và ngoài của một góc thì vuông góc với nhau. Do đó BM \perp BN\(BM \perp BN\). Áp dụng công thức

Từ khóa » Học Vnen Toán 9