SOLVED:Compute \sinh (\ln 5) And \tanh (3 \ln 5) Without Using A ...

This problem has been solved by verified expert Dishary Hossain 100% free to try See Answer

Question

Compute $\sinh (\ln 5)$ and $\tanh (3 \ln 5)$ without using a calculator. Compute $\sinh (\ln 5)$ and $\tanh (3 \ln 5)$ without using a calculator. Calculus for AP Jon Rogawski & Ray… 2nd Edition Chapter 1, Problem 36 View All Chapters

Step 1

Step 1: We start by using the definition of the hyperbolic sine function: \[\sinh(x) = \frac{e^x - e^{-x}}{2}\] So, we have: \[\sinh(\ln 5) = \frac{e^{\ln 5} - e^{-\ln 5}}{2}\] Show more…

Show all steps

Please give Ace some feedback

Your feedback will help us improve your experience

Submit Thanks for your feedback! Compute $\sinh (\ln 5)$ and $\tanh (3 \ln 5)$ without using a calculator. Play audio Feedback Powered by NumerAI

Dishary Hossain and 58 other Calculus 1 / AB educators are ready to help you.

Ask a new question

Labs

Want to see this concept in action?

NEW

Explore this concept interactively to see how it behaves as you change inputs.

View Labs

Key Concepts

Exponential and Logarithmic Identities Exponential and logarithmic identities are core tools in simplifying expressions that involve exponential and logarithm functions. A key identity is that e^(ln x) equals x, and more generally, e^(a ln x) equals x^a. This relationship is fundamental to transforming expressions like sinh(ln x) or tanh(3 ln x) into forms that can be easily simplified, showing the interplay between exponentiation and logarithms. Hyperbolic Functions Hyperbolic functions, including sinh and tanh, are analogous to the trigonometric functions but are defined using exponential functions. They are essential in various branches of mathematics and physics, particularly in solving differential equations and describing hyperbolic geometry. Understanding their definitions—involving combinations of exponential functions—allows one to simplify and compute their values without numerical computation.

Recommended Videos

Evaluate each logarithm without using a calculator. $$\ln e^{5 / 3}$$

Nonlinear Functions

Logarithmic Functions

Evaluate each logarithm without using a calculator. $$ \ln e^{5 / 3} $$

Nonlinear Functions

Logarithmic Functions

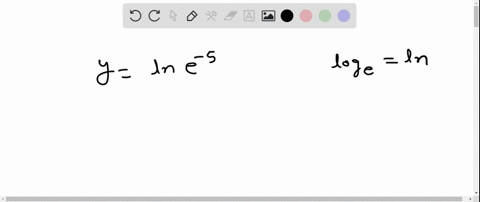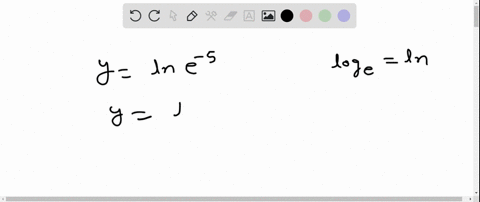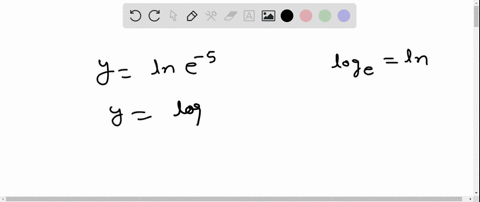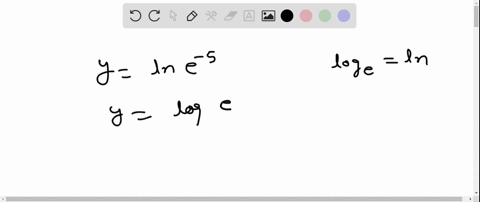
Evaluate the expression without using a calculator. $$ \ln e^{-5} $$

Functions and Graphs

Logarithmic Functions

Transcript

00:01 So we will solve the following sign of national log of 5 and tangent of 3, natural log of 5 without using a calculator through the method of using these following hyperbolic functions as seen in the textbook. 00:18 And to calculate what the hyperbolic function would be for tangent, we know that tangent is simply equal to the sign over cosine. 00:27 So that's exactly what i did. 00:29 I divided this by this to get this following equation. 00:37 So let's work on the first half of this problem, sign of a national log of 5. 00:42 What i did was i treated the natural log of 5 as x, and i plugged that into the hyperbolic function for a sign to get this following equation. 00:53 Sign of the national log of 5 equals e to the national of 5 minus, minus e to the natural log, or to the negative natural log of 5 all over 2. 01:06 And when i look at this portion of the problem, i know that this is the same exact value as negative e to the natural log of 1 5th. 01:27 And now that we've clarified that, we can simplify it even further, because when we have the e, to the natural log of something, it will simplify to whatever is in the parentheses for the natural log. 01:44 So this formula will turn into 5 minus 1 5th, all over 2. 01:58 And we can turn this into 25 over 5 for the least common denominator, one fifth while over two. 02:17 So it's 24 over five divided by two. 02:28 So we get our answer as 24 over 10. 02:39 Great. 02:41 Let's use the same principles on our tangent function... Need help? Use Ace Ace is your personal tutor. It breaks down any question with clear steps so you can learn. Start Using Ace Ace is your personal tutor for learning Step-by-step explanations Instant summaries Summarize YouTube videos Understand textbook images or PDFs Study tools like quizzes and flashcards Listen to your notes as a podcast

What our educators say

25992 Students Helped in Calculus 1 / AB “Numerade has a great goal - to increase people's educational levels all around the world. Educators do not complete student's personal homework tasks. We create video tutorials that may be used for many years in the future.” Dr. Mei Lin Chen PhD in Calculus 1 / AB

44601 Students Helped in Calculus 1 / AB "The format has forced me to think about what knowledge is needed by the student to solve a problem and present it concisely and understandably within the time constraint of the video." Dr. Emily Green PhD in Calculus 1 / AB

30417 Students Helped in Calculus 1 / AB “Explaining topics while I make Numerade videos has helped me deepen my own understanding and come up with new ways to help my students grasp concepts while I'm teaching.” Professor Jonathan Reed Master's in Calculus 1 / AB

Get step-by-step video solutionfrom top educators Start your free 7-day trial, Sign up now. Continue with Facebook Continue with Apple Continue with Clever or Name Email Password Create Account By creating an account, you agree to the Terms of Service and Privacy Policy Already have an account? Log In A free answerjust for you

Watch the video solution with this free unlock.

View the Answer

Log in to watch this video ...and 100,000,000 more!

EMAIL

PASSWORD

Log in OR Continue with Facebook Continue with Apple Continue with Clever Don't have an account? Sign Up