Some Important Results - Study Material For IIT JEE - AskIITians

Some Important Results

1. Differentiating (1+x)n = C0 + C1x + C2x2 +...+ Cnxn of both sides we have,

n(1 + x)n-1 = C1 + 2C2x + 3C3x2 +...+ nCnxn-1. ... (E)

Put x = 1 in (E) so that n2n+1 = C1 + 2C2 + 3C3 + ...+ nCn.

Put x = -1 in (E) so that 0 = C1 - 2C2 +...+ (-1)n-1 nCn.

Differentiating (E) again and again we will have different results.

2. Integrating (1 + x)n, we have,

((1+x)n+1)/(n+1) + C = C0x + C1x2/2 + C2x3/3 +.....+Cnxn+1/(n+1) (where C is a constant)

For x = 0, we get C = -1/(n+1) .

Therefore ((1+x)n+1 - 1)/(n+1) = C0x + C1x2/2 + C2x3/3 +.....+Cnxn+1/(n+1) ..... (F)

Put x = 1 in (F) and get

(2n+1 - 1)/n+1= C0 + C1/2 +...Cn/n+1 .

Put x = -1 in (F) and get, 1/n+1 = C0 - C1/2 + C2/3 - ......

Put x = 2 in (F) and get, (3n+1-1)/n+1 = 2 C0 + 22/2 C1 + 22/3 C2 +...+ 2n+1/n+1 = Cn.

Problems Related to Series of Binomial Coefficients in Which Each Term is a Product of an Integer and a Binomial Coefficient, i.e. In the Form k.nCr.

Illustration:

If (1+x)n =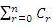xr then prove that C1 + 2C2 + 3C3 +...+ nCn = n2n-1.

Solution:

Method (i) : rth term of the given series

rth term of the given series, tr = nCr

=> tr = r × n/r × n-1Cr-1 = n × n-1Cr-1 (because nCr =n/r .n-1Cr-1)

Sum of the series =

Put x = 1 in the expansion of (1 + x)n-1, so that

(n-1C0 + n-1C1 +...+ n-1Cn-1) = 2n-1

=> = n.2n-1.

Method (ii) : By Calculus

We have (1 + x)n = C0 + C1x + C2x2 +...+ Cnxn. ... (1)

Differentiating (1) w.r.t. x, we get

n(1 + x)n-1 = C1 + 2C2x + 3C3 x2 +...+ n Cnxn-1. ... (2)

Putting x = 1 in (2), we have, n 2n-1 = C1 + 2C2 +....+ nCn. ... (3)

Illustration:

If (1+ x)n =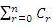 xr then prove that C0 + 2.C1 + 3.C2+...+(n+1)Cn=2n-1(n+2).

Solution:

Method (i): rth term of the given series

rth term of the given series

tr = nCr-1 = [(r-1) + 1]. nCr-1

= (r-1) nCr-1 + nCr-1 = n. n-1Cr-2 + nCr-1 (because nCr-1 =n/(r-1) . n-1Cr-2)

Sum of the series =

= n[n-1C0 + n-1C1 +...+ n-1Cn-1]+[nC0 + nC1 +...+ nCn] = n.2n-1 + 2n = 2n-1 (n+2).

Method (ii) by Calculus.

We have (1 + x)n = C0 + C1x + C2x2 +...+ Cnxn. ... (1)

Multiplying (1) with x, we get

x(1+x)n = C0x + C1x2 + C2x3 +...+ Cnxn+1. ... (2)

Differentiating (2) w.r.t. x, we have

(1 + x)n + n(1 + x)n-1 x = C0x + 2C1x2 +...+ (n+1)Cnxn ... (3)

Putting x = 1 in (3), we get

2n + n.2n-1 = C0 + 2C1 + 3C2 +...+ (n+1)Cn

=> C0 + 2C1 + 3C2 +...+ (n+1)Cn = 2n-1 (n+2).

Problems Related to Series of Binomial Coefficient in Which Each Term is Binomial Coefficient divided by an Integer, i.e. in the Form of nCr/k.

Illustration:

If (1+x)n =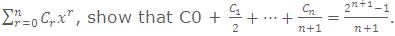

Solution:

Method (i) : rth term of the given series

Method (ii): By Calculus

(1+x)n = C0 + C1x + C2x2 +...+ Cnxn ... (1)

Integrating both the sides of (1) w.r.t. x between the limits 0 to x, we get

... (2)

Substituting x = 1 in (2), we get 2n+1/n+1 = C0 + c1/2 + c2/3 +.....+ cn/n+1.

Illustration:

If (1+x)n =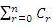 xr ,show that

Method I : rth term of the given series Tr =

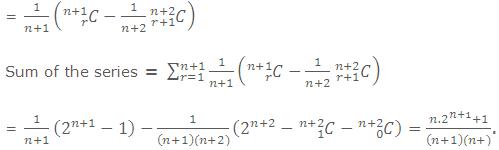
Method II : (By Calculus)

(1 + x)n = C0 + C1x + C2x2 +...+ Cnxn

=> x(1+x)n = C0x + C1x2 + C2x3 +...+ Cnxn+1 ... (1)

Integrating both the sides of (1) with respect to x

Put x = 0, => k = 1/((n+1)(n+2))

Put x = 1,

.

Problem Related to Series of Binomial Coefficients in Which Each Term is a Product of two Binomial Coefficients.

(a) If sum of lower suffices of binomial expansion in each term is the same

i.e. nC0 nCn + nC1 nCn-1 + nCn-2 +...+ nCn nC0

i.e. 0 + n = 1 + (n-1) = 2 + (n-2) = n + 0.

Then the series represents the coefficients of xn in the multiplication of the following two series

(1+x)n = C0 + C1x + C2x2 +...+ Cnxn

and (1+x)n = C0 + C1x + C2x2 +...+ Cnxn.

Illustration:

Prove that C0Cr + C1Cr+1 + C2Cr+2 +...+ Cn-r Cn = (2n)!/((n-r)!(n+r)!)

Solution:

We have,

C0 + C1x + C2x2 + ... + Cnxn = (1+x)n ... (1)

Also C0xn + C2xn-2 +...+ Cn = (x+1)n ... (2)

Multiplying (1) and (2), we get

(C0 + C1x2 +...+ Cnxn)(C0xn + C1xn-2 + C2xn-2 +...+ Cn) = (1+x)2n ... (3)

Equating coefficient of xn-r from both sides of (3), we get

C0Cr + C1Cr+1 + C2Cr+2 +...+ Cn-rCn = 2nCn-r = (2n)/((n-r)!(n+r)!) .

Illustration:

Prove that Co2 + C12 +...+ Cn2 = (2n)!/n!n! .

Solution:

Since

(1 + x)n = C0 + C1x + C2x2 +...+ Cnxn, ... (1)

(x + 1)n = C0xn + C1xn-2 +...+ Cn, ... (2)

(C0 + C1x + C2x2 +...+ Cnxn)(C0xn + C1xn-1 + C2xn-2 +...+ Cn)=(1+x)2n.

Equating coefficient of xn, we get

C02 + C12 + C22 +...+ Cn2 = 2nCn = (2n)!/n!n! .

Illustration:

If (1+x)n = , then prove that

mCr nC0 + mCr-1 nC1 + mCr-2 nC2 +...+ mC1 nCr-1 + mC0 nCr = m+nCr

where m, n, r are positive integers and r < m and r < n.

Solution:

(1+x)n = nC0 + nC1x + nC2x2 +...+ nCrxr +...+ nCnxn ... (1)

and also

(1+x)m = mC0 + mC1x + mC2x2 +...+ mCrxr +...+ mCmxm ... (2)

Multiplying (1) and (2), we get

(nC0 + nC1x + nC2x2 +...+ nCrxr +...+ nCnxn)x

(mC0 + mC1x + mC2x2 +...+ mCrxr +...+ mCmxm) = (1+x)m+n

= m+nC0 + m+2C1x + m+nC2x2 +...+ m+nCrxr +...+ m+nCm+nxm+n

Equating the coefficient of xr, we get

mCr nC0 + mCr-1 nC1 + mCr-2 nC2 +...+ mC1 nCr-1 + mC0 nCr = m+nCr

(b) If one series has constant lower suffices and other has varying lower suffices

Illustration:

Prove that nC0.2nCn - nC12n-2Cn + nC2/2n-4Cn -...= 2n.

Solution:

nC0.2nCn - nC12n-2Cn + nC2/2n-4Cn -...

= coefficient of xn in[nC0(1+x)2n - nC1(1+x)2n-2+nC2(1+x)2n-4 - ...]

= coefficient of xn in

[nC0((1+x)2)n - nC1((1+x)2)n-1 + nC2((1+x)2)n-2 - ...]

= coefficient of xn in [(1+x)2 - 1]n

= coefficient of xn in (2x+x2)n = co-efficient of xn in xn (2+x)n = 2n.

At askIITians we provide you free study material on Set Theory and Functions and you get all the professional help needed to get through IIT JEE and AIEEE easily. AskIITians also provides live online IIT JEE preparation and coaching where you can attend our live online classes from your home!