Tách Tam Thức Bậc 2 Hoặc Bậc 3 (lớp 8): X^3 X 2 - Hoc24

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay

• Phú Nguyễn Duy

25 tháng 7 2018 lúc 11:34

tách tam thức bậc 2 hoặc bậc 3 (lớp 8): x^3 + x + 2

Xem chi tiết Lớp 8 Toán Violympic toán 8 2 0 Gửi Hủy Phạm Tuấn Đạt 30 tháng 8 2018 lúc 21:46

\(x^3+x+2\)

\(=x^3+x^2-x^2-x+2x+2\)

\(=x^2\left(x+1\right)-x\left(x+1\right)+2\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-x+2\right)\)

Đúng 0 Bình luận (0) Gửi Hủy Bùi Mạnh Khôi 30 tháng 8 2018 lúc 22:33

\(x^3+x+2\)

\(=x^3-x+2x+2\)

\(=x\left(x^2-1\right)+2x+2\)

\(=x\left(x-1\right)\left(x+1\right)+2\left(x+1\right)\)

\(=\left(x^2-x\right)\left(x+1\right)+2\left(x+1\right)\)

\(=\left(x^2-x+2\right)\left(x+1\right)\)

Đúng 0 Bình luận (0) Gửi Hủy

• Nguyễn An

27 tháng 7 2017 lúc 9:53

Có cách nào để tách đa thức bậc 3 trở lên thành nhân tử cho lớp 8 mà không cần dùng máy tính không?ví dụ như câu này: x^4+x^3+6.x^2+5.x+5 hoặc câu này x^3.y^3+x^2.y^2+4

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Lê Quỳnh Mai

26 tháng 7 2015 lúc 14:09

Phân tích đa thức thành nhân tử bằng cách tách hạng tử bậc nhất:   x^2 - 11x + 8

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 1 0 Gửi Hủy Trần Thị Loan 26 tháng 7 2015 lúc 14:25

= [x2 - 2.x.\(\frac{11}{2}\) + \(\left(\frac{11}{2}\right)^2\)] - \(\frac{121}{4}\)+ 8 = (x - \(\frac{11}{2}\))2 - \(\frac{89}{4}\) =  (x - \(\frac{11}{2}\))2 - \(\left(\frac{\sqrt{89}}{2}\right)^2\)

= \(\left(x-\frac{11}{2}-\frac{\sqrt{89}}{2}\right).\left(x-\frac{11}{2}+\frac{\sqrt{89}}{2}\right)\)= \(\left(x-\frac{11+\sqrt{89}}{2}\right).\left(x+\frac{\sqrt{89}-11}{2}\right)\)

Đúng 0 Bình luận (0) Gửi Hủy

• Thực hành 1
• 

SGK Chân trời sáng tạo trang 6,7 26 tháng 9 2023 lúc 23:09

Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).

a) \(f\left( x \right) = 2{x^2} + x - 1\);

b) \(g\left( x \right) =  - {x^4} + 2{x^2} + 1\)

c) \(h\left( x \right) =  - {x^2} + \sqrt 2 .x - 3\)

Xem chi tiết Lớp 10 Toán Bài 1: Dấu của tam thức bậc hai 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 26 tháng 9 2023 lúc 23:09

a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai

          \(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)

b) Biểu thức \(g\left( x \right) =  - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai

c) Biểu thức \(h\left( x \right) =  - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai

          \(h\left( 1 \right) =  - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2  - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)

Đúng 0 Bình luận (0) Gửi Hủy

• Bài 1.39
• 

SGK Kết nối tri thức với cuộc sống - Trang 27 21 tháng 7 2023 lúc 15:06

Đơn thức \( - {2^3}{x^2}y{z^3}\) có:

A. Hệ số -2, bậc 8

B. Hệ số \( - {2^3}\), bậc 5

C. Hệ số -1, bậc 9

D. Hệ số \( - {2^3}\), bậc 6 

Xem chi tiết Lớp 8 Toán Bài tập cuối chương 1 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 12 tháng 1 2024 lúc 21:13

Đơn thức \( - {2^3}{x^2}y{z^3}\) có hệ số là \( - {2^3}\), bậc là 2+1+3=6.

Chọn D.

Đúng 0 Bình luận (0) Gửi Hủy

• Trần Lam An

4 tháng 5 2020 lúc 23:39

Bài 1: xét dấu tam thức bậc hai

1.f(x)= -1/2 x^2

2.f(x)=x^2-2x-1

3.v=-x^2-4x+1

4.v=x^2+x+1

5.v=-x^2+4x+6

6.y= căn bặc hai 2x^2

7.y=((1-căn bậc hai 2)x^2-2x-1

8.v=2(x+3)^2-5

9.v= trừ căn bậc hai 2^2+4x

Xem chi tiết Lớp 10 Toán §5. Dấu của tam thức bậc hai 0 0 Gửi Hủy

• Bài 1
• 

SGK Chân trời sáng tạo trang 9 26 tháng 9 2023 lúc 23:11

Đa thức nào sau đây là tam thức bậc hai?

a) \(4{x^2} + 3x + 1\)

b) \({x^3} + 3{x^2} - 1\)

c) \(2{x^2} + 4x - 1\)

Xem chi tiết Lớp 10 Toán Bài 1: Dấu của tam thức bậc hai 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 26 tháng 9 2023 lúc 23:12

a) Đa thức \(4{x^2} + 3x + 1\) là tam thức bậc hai

b) Đa thức \({x^3} + 3{x^2} - 1\) không là tam thức bậc hai

c) Đa thức \(2{x^2} + 4x - 1\) là tam thức bậc hai

Đúng 0 Bình luận (0) Gửi Hủy

• Luyện tập 2
• 

SGK Kết nối tri thức với cuộc sống trang 19-22 30 tháng 9 2023 lúc 23:30

Xét dấu các tam thức bậc hai sau:

a) \( - 3{x^2} + x - \sqrt 2 \) 

b) \({x^2} + 8x + 16\) 

c) \( - 2{x^2} + 7x - 3\)

Xem chi tiết Lớp 10 Toán Bài 17: Dấu của tam thức bậc hai 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 30 tháng 9 2023 lúc 23:30

a) \(f(x) =  - 3{x^2} + x - \sqrt 2 \)có \(\Delta  = 1 - 12\sqrt 2  < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)

b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta  = 0\)và a=1>0 nên g(x) có nghiệm kép \(x =  - 4\) và g(x) >0 với mọi \(x \ne  - 4\)

c) \(h(x) =  - 2{x^2} + 7x - 3\) có \(\Delta  = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)

Do đó ta có bảng xét dấu h(x)

Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)

Đúng 0 Bình luận (0) Gửi Hủy

• Nguyễn cẩm linh

7 tháng 7 2016 lúc 8:47

Tìm x để các bt có nghĩa vd : căn bậc hai của 7x+3 = 7x+3 lớn hơn hoặc bằng x tương đương x lớn hơn hoặc bằng -3 phần 7

 

Căn bậc hai của 1 phần x-3

Căn bậc hai của -3 phần 2-x

Xem chi tiết Lớp 9 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Hoạt động 3
• 

SGK Cánh Diều trang 44,45 23 tháng 9 2023 lúc 11:42 a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 3x + 2 tùy theo các khoảng của x.b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai fleft( x right)   - {x^2} + 4x - 3 tùy theo các khoảng của x.c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số tùy theo các khoảng của x trong trường hợp Delta  0.Đọc tiếp

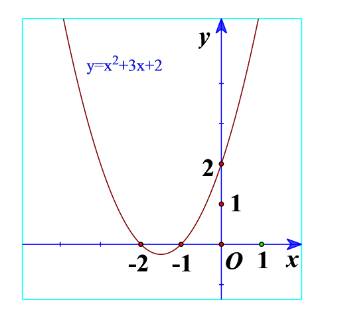
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.

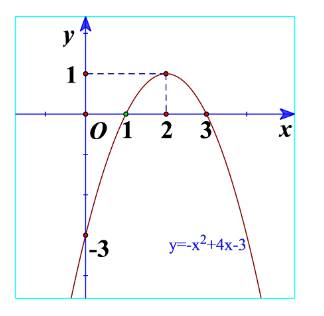
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) =  - {x^2} + 4x - 3\) tùy theo các khoảng của x.

c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta  > 0\).

Xem chi tiết Lớp 10 Toán $3. Dấu của tam thức bậc hai 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 23 tháng 9 2023 lúc 11:42

a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành

=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)

Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành

=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)

Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành

=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)

b)

Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành

=> \(f\left( x \right) =  - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)

Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành

=> \(f\left( x \right) =  - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)

Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành

=> \(f\left( x \right) =  - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)

c) Nếu \(\Delta  > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).

Đúng 0 Bình luận (0) Gửi Hủy