Tài Liệu Tự Học Hàm Số Lượng Giác Và Phương Trình Lượng Giác

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Đề thi
  • Học tiếng Anh
  • Giáo án
  • Bài giảng điện tử
  • Tài liệu Giáo viên
  • Tập huấn Giáo viên

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Download.vn Học tập Lớp 11 Toán 11 Tài liệu tự học hàm số lượng giác và phương trình lượng giác Tài liệu ôn tập môn Toán lớp 11 Tải về Bình luận

• 4

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo

Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua Zalo

Download.vn xin giới thiệu đến các bạn tài liệu Tài liệu tự học hàm số lượng giác và phương trình lượng giác được chúng tôi tổng hợp và đăng tải ngay sau đây.

Tài liệu bao gồm 60 trang với nội dung được chia thành ba phần: Kiến thức cần nắm; Dạng bài tập có hướng dẫn giải và bài tập đề nghị; Phần trắc nghiệm có đáp án. Hy vọng với tài liệu này các bạn học sinh lớp 11 có thêm nhiều tài liệu học tập, củng cố kiến thức để đạt được kết quả trong các bài kiểm tra, bài thi học kì 1 sắp tới. Ngoài ra các bạn tham khảo thêm một số tài liệu như: Bài tập trắc nghiệm lượng giác vận dụng cao, Phương pháp giải phương trình lượng giác, Trắc nghiệm nâng cao hàm số lượng giác và phương trình lượng giá. Nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Tài liệu hàm số lượng giác và phương trình lượng giác

Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1 Chương I. HSLG & PTLG Phần Tự Luận CHƯƠNG I ---0o0--- HÀM SỐ LƯỢNG GIÁC & PHƯƠNG TRÌNH LƯỢNG GIÁC---0O0--- ÔN TẬP CÔNG THỨC LƯỢNG GIÁC 1. Hằng đẳng thức lượng giác cơ bản 22sincos1αα+=  sintan;,cos2kkαπααπα=≠+∈ℤ coscot;,sinkkαααπα=≠∈ℤ  tan.cot1;,2kkπααα=≠∈ℤ 2211tan;,2coskkπααπα+=≠+∈ℤ  2211cot;,sinkkααπα+=≠∈ℤ 2. Các công thức lượng giác 2.1. Công thức cộng ()coscoscossinsinαβαβαβ±=∓()sinsincoscossinαβαβαβ±=±()tantantan1tantanαβαβαβ±±=∓, với mọi ,αβ làm cho các biểu thức có nghĩa. 2.2. Công thức nhân đôi sin22sincosααα= 2222cos2cossin2cos112sinααααα=−=−=− 22tantan2;,2,21tankkαπαααπα=≠+∈−ℤ 2.3. Công thức nhân ba 3cos34cos3cosααα=−  3sin33sin4sinααα=−2.4. Công thức hạ bậc 21cos2cos2αα+=  21cos2sin2αα−= 21cos2tan1cos2ααα−=+, với α làm cho biểu thức có nghĩa. 2.6. Công thức biến đổi tổng thành tích coscos2cos.cos22αβαβαβ+−+=  coscos2sin.sin22αβαβαβ+−−=− sinsin2sin.cos22αβαβαβ+−+= sinsin2cos.sin22αβαβαβ+−−= , với mọi ,αβ làm cho các biểu thức có nghĩa. 2.7. Công thức biến đổi tích thành tổng ()()1cos.coscoscos2αβαβαβ=++− ()()1sin.sincoscos2αβαβαβ= −+−− ()()1sin.cossinsin2αβαβαβ=++− 2.8. Công thức rút gọn 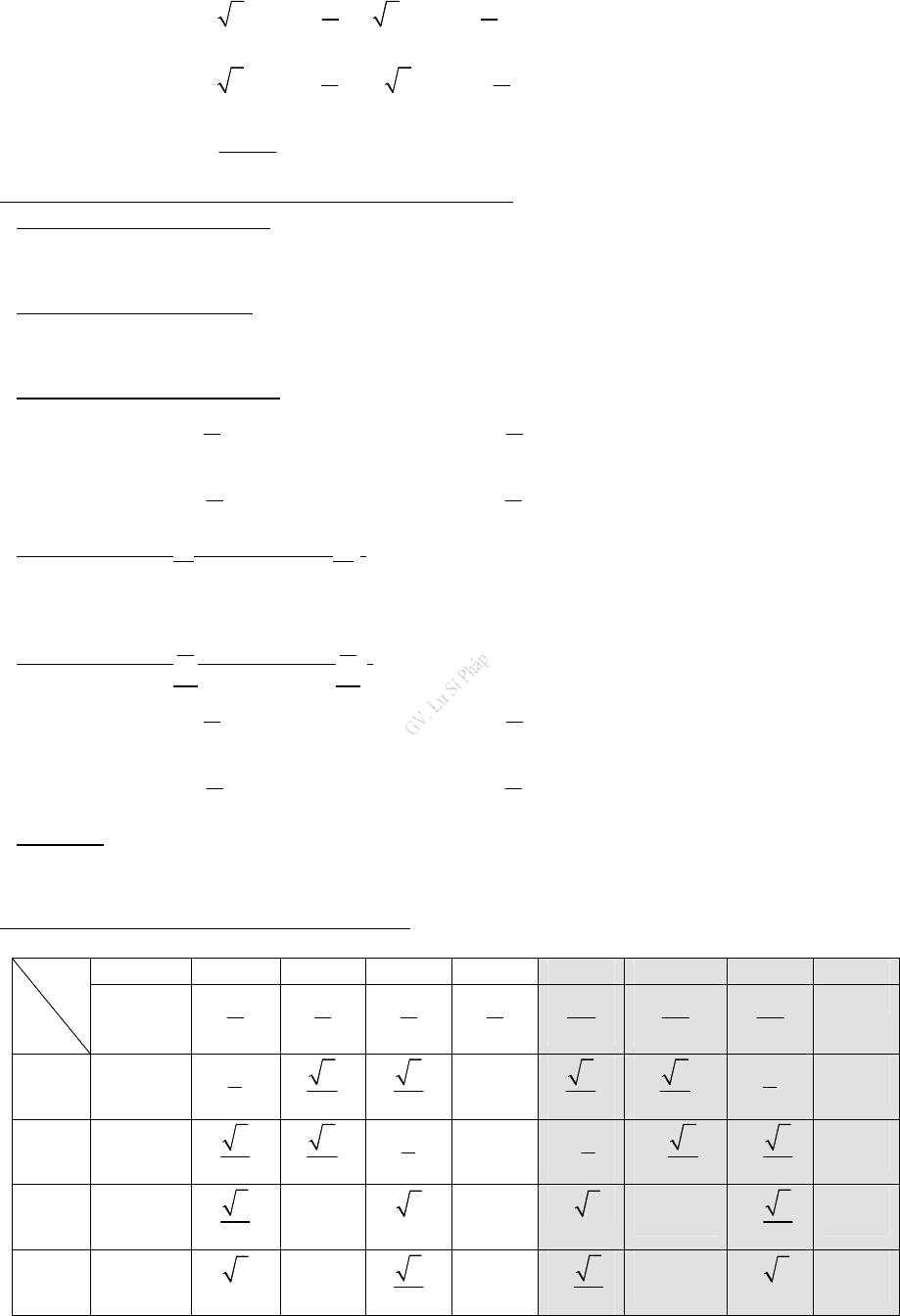Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2 Chương I. HSLG & PTLG Phần Tự Luận sincos2sin2 cos44ππαααα+=+=− sincos2sin2cos44ππαααα−=−= −+ 2tancotsin2ααα+=, với α làm cho biểu thức có nghĩa 3. Giá trị lượng giác của các góc (cung) có liên quan đặt biệt 3.1. Hai góc đối nhau ( cung đối) (α làm cho các biểu thức có nghĩa) cos()cosαα−=  sin()sinαα−= − tan()tanαα−= −  cot()cotαα−= − 3.2. Hai góc bù nhau( cung bù)(α làm cho các biểu thức có nghĩa) sin()sinπαα−=  cos()cosπαα−= − tan()tanπαα−= −  cot()cotπαα−= − 3.3. Hai góc phụ nhau ( cung phụ)(α làm cho các biểu thức có nghĩa) sincos2παα−=  cossin2παα−= tancot2παα−=  cottan2παα−= 3.4. Hai góc hơn kém π(cung hơn kém π),(α làm cho các biểu thức có nghĩa) sin()sinπαα+= −  cos()cosπαα+= − tan()tanπαα+=  cot()cotπαα+= 3.5. Hai góc hơn kém 2π(cung hơn kém 2π),(α làm cho các biểu thức có nghĩa) sincos2παα+=  cossin2παα+= − tancot2παα+= −  cottan2παα+= − 3.6. Cung bội. (k∈ℤ, α làm cho các biểu thức có nghĩa) sin(2)sinkαπα+=  cos(2)coskαπα+= tan()tankαπα+=  cot()cotkαπα+= 4. Bảng giá trị lượng giác các góc (cung) đặt biệt α HSLG 00 300 450 600 900 1200 1350 1500 1800 0 6π 4π 3π 2π 23π 34π 56π π sinα 0 12 22 32 1 32 22 12 0 cosα 1 32 22 12 0 12− 22− 32− - 1 tanα 0 33 1 3 || 3− - 1 33− 0 cotα || 3 1 33 0 33− - 1 3− || || : Không xác định 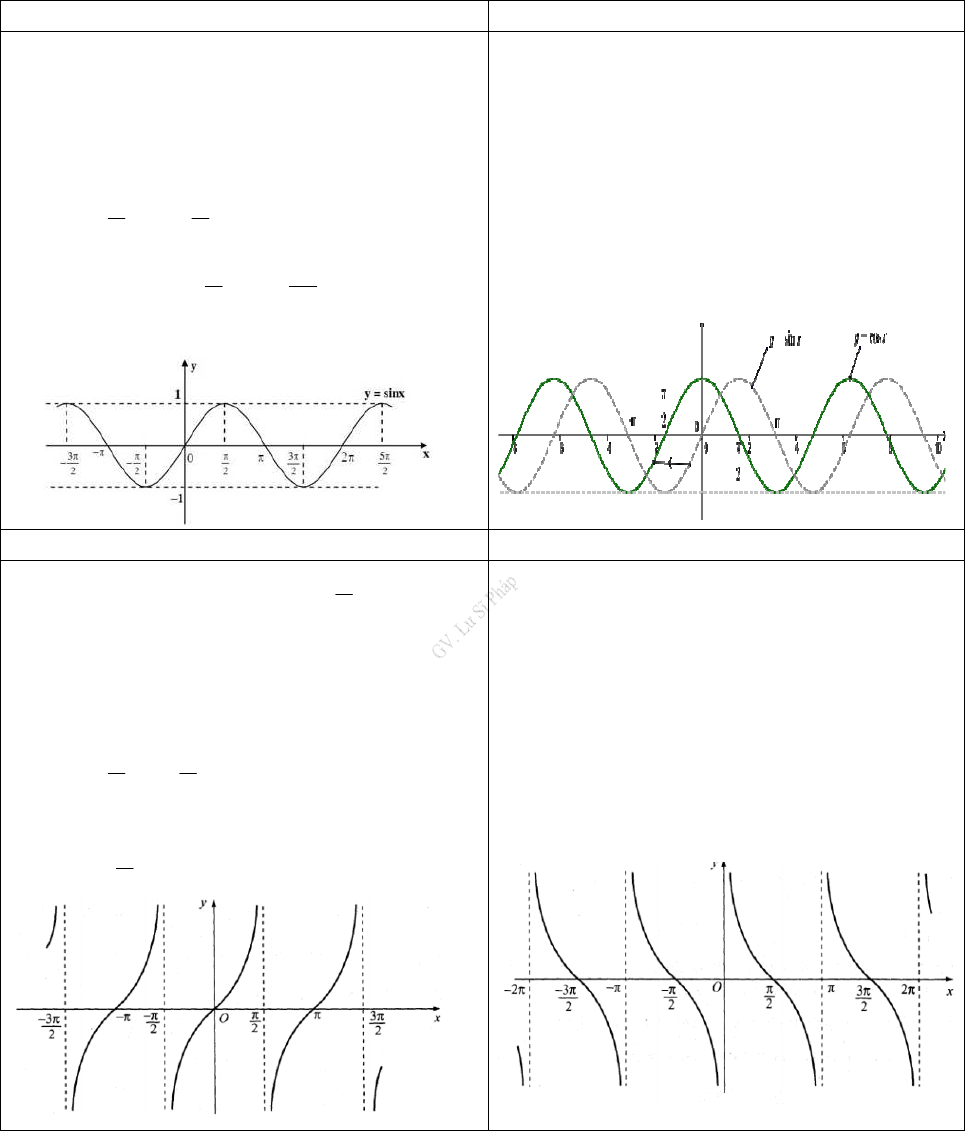Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 3 Chương I. HSLG & PTLG Phần Tự Luận §1. HÀM SỐ LƯỢNG GIÁC A.KIẾN THỨC CẦN NẮM Hàm số sinyx= Hàm số cosyx= • Có tập xác định là ℝ • Có tập giá trị là 1;1− • Là hàm số lẻ • Là hàm số tuần hoàn với chu kì 2Tπ= • Đồng biến trên mỗi khoảng 2;222kkππππ−++ và nghịch biến trên mỗi khoảng 32;2,22kkkππππ++∈ℤ • Có đồ thị là một đường hình sin • Có tập xác định là ℝ • Có tập giá trị là 1;1− • Là hàm số chẵn • Là hàm số tuần hoàn với chu kì 2Tπ= • Đồng biến trên mỗi khoảng ()2;2kkπππ−+ và nghịch biến trên mỗi khoảng ()2;2,kkkπππ+∈ℤ • Có đồ thị là một đường hình sin Hàm số tanyx= Hàm số cotyx= • Có tập xác định là1\,2Dkkππ=+∈ℝℤ • Có tập giá trị là ℝ • Là hàm số lẻ • Là hàm số tuần hoàn với chu kì là π • Đồng biến trên mỗi khoảng ;;22kkkππππ−++∈ℤ • Có đồ thị nhận mỗi đường thẳng ;2xkkππ=+∈ℤ làm một đường tiệm cận • Có tập xác định là {}2\,Dkkπ=∈ℝℤ • Có tập giá trị là ℝ • Là hàm số lẻ • Là hàm số tuần hoàn với chu kì là π • Nghịch biến trên mỗi khoảng ();;kkkπππ+∈ℤ • Có đồ thị nhận mỗi đường thẳng ;xkkπ=∈ℤ làm một đường tiệm cận B.BÀI TẬP ạng 1. Tập xác định của hàm số- Hàm số xác định với một điều kiện - Hàm số xác định bởi hai hay nhiều điều kiện - Hàm số sin;cosyxyx== có tập xác định là ℝ - Hàm số tanyx=xác định khi và chỉ khicos0x≠; Hàm số cotyx=xác định khi và chỉ khisin0x≠ D Chia sẻ bởi: Trịnh Thị Thanh

Tải về

Liên kết tải về Tài liệu tự học hàm số lượng giác và phương trình lượng giác 1,2 MB Tải về Tìm thêm: Toán 11 Phương trình lượng giác

Có thể bạn quan tâm

• 

  Văn mẫu lớp 10: Cảm nhận về bài thơ Nhàn của Nguyễn Bỉnh Khiêm

  100.000+
• 

  Các thể thơ Việt Nam - Cách xác định thể thơ

  100.000+ 3
• 

  Cảm nhận khổ thơ đầu bài Mùa xuân nho nhỏ của Thanh Hải

  100.000+ 2
• 

  Nghị luận về vai trò của sách đối với đời sống nhân loại

  100.000+ 4
• 

  Phân tích hình ảnh nữ thanh niên xung phong trong Những ngôi sao xa xôi (Sơ đồ tư duy)

  100.000+
• 

  Kết bài chung cho nghị luận văn học lớp 12

  50.000+
• 

  Phân tích khổ 3 bài thơ Tây Tiến của Quang Dũng

  100.000+
• 

  Dàn ý viết bài văn kể lại một chuyến đi đáng nhớ của em

  100.000+
• 

  So sánh Cách mạng tư sản Anh, Chiến tranh giành độc lập của 13 thuộc địa Anh ở Bắc Mỹ, Cách mạng tư sản Pháp

  10.000+ 1
• 

  Đề thi thử THPT Quốc gia năm 2025 môn Địa lí Sở GD&ĐT Thái Nguyên

  1.000+

Xem thêm

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Khiếu nại & Hoàn tiền

Giải quyết vấn đề đơn hàng & hoàn trả

Mới nhất trong tuần

• Trả lời ngắn Toán 11: Phương trình lượng giác

  

• Trắc nghiệm đúng sai Toán 11: Giới hạn của hàm số

  

• Trắc nghiệm đúng sai Toán 11: Hàm số lượng giác

  

• Trắc nghiệm đúng sai Toán 11: Quan hệ song song trong không gian

  

• Trắc nghiệm đúng sai Toán 11: Phương trình lượng giác cơ bản

  

• Trả lời ngắn Toán 11: Hàm số lượng giác

  

• Trả lời ngắn Toán 11: Dãy số

  

• Trả lời ngắn Toán 11: Góc lượng giác

  

• Trả lời ngắn Toán 11: Giá trị lượng giác của góc lượng giác

  

• Trả lời ngắn Toán 11: Công thức lượng giác

  

Đóng Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ Nhắn tin Zalo

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.