Tập Nghiệm Của Bất Phương Trình

Có thể bạn quan tâm

- - Mầm non
  - Lớp 1
  - Lớp 2
  - Lớp 3
  - Lớp 4
  - Lớp 5
  - Lớp 6
  - Lớp 7
  - Lớp 8
  - Lớp 9
  - Lớp 10
  - Lớp 11
  - Lớp 12
  - Thi vào lớp 6
  - Thi vào lớp 10
  - Thi Tốt Nghiệp THPT
  - Đánh Giá Năng Lực
  - Khóa Học Trực Tuyến
  - Hỏi bài
  - Trắc nghiệm Online
  - Tiếng Anh
  - Thư viện Học liệu
  - Bài tập Cuối tuần
  - Bài tập Hàng ngày
  - Thư viện Đề thi
  - Giáo án - Bài giảng
  - Tất cả danh mục
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 10 Toán lớp 10 Chuyên đề Toán 10 Tập nghiệm của bất phương trình Tìm tập nghiệm của bất phương trình lớp 10 Bài trước Tải về Bài sau Lớp: Lớp 10 Môn: Toán Dạng tài liệu: Chuyên đề Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Bất phương trình Toán 10

1. Tập nghiệm S của bất phương trình là gì?
2. Bài tập ví dụ minh họa
3. Bài tập tự rèn luyện

Trong chương trình Toán lớp 10, chuyên đề Tập nghiệm của bất phương trình là một trong những nội dung nền tảng và có mặt xuyên suốt trong các bài kiểm tra, bài tập tự luận, trắc nghiệm lẫn đề thi học kỳ. Việc xác định tập nghiệm không chỉ giúp học sinh nắm chắc bản chất của bất phương trình mà còn là kỹ năng quan trọng để làm tốt các chuyên đề nâng cao sau này như: bất phương trình chứa căn, chứa trị tuyệt đối, hệ bất phương trình hay bất phương trình bậc hai.

Bài viết này được xây dựng nhằm giúp bạn:

Hiểu rõ khái niệm tập nghiệm và ý nghĩa của nó trong giải toán;
Nắm trọn các phương pháp giải bất phương trình lớp 10 từ cơ bản đến nâng cao;
Phân biệt chính xác các dạng bất phương trình thường gặp;
Rèn luyện kỹ năng tìm tập nghiệm qua ví dụ minh họa – bài tập tự luyện – đáp án chi tiết;
Tăng tốc độ làm bài, hạn chế sai lầm khi biểu diễn nghiệm trên trục số.

Nếu bạn đang học Toán 10, chuẩn bị kiểm tra định kỳ, hoặc đang tìm tài liệu chuẩn để “nằm lòng” dạng toán này, bài viết sẽ là trợ thủ đáng tin cậy giúp bạn học nhanh – hiểu sâu – vận dụng linh hoạt.

Tài liệu do VnDoc.com biên soạn và đăng tải, nghiêm cấm các hành vi sao chép với mục đích thương mại.

Tìm tập nghiệm của bất phương trình

1. Bất phương trình

Trước hết ta xét đến định nghĩa bất phương trình một ẩn

Định nghĩa:

Bất phương trình một ẩn là một mệnh đề chứa biến x so sánh hai hàm số f(x) và g(x) trên trường số thực dưới một trong các dạng

$f(x) < g(x), f(x) > g(x); f(x) ≥ g(x); f(x) ≤ g(x)$

Giao của hai tập xác định của các hàm số f(x) và g(x) được gọi là tập xác định của bất phương trình.
Nếu với giá trị x =a, f(a) > 0 là bất đẳng thức đúng thì ta nói rằng a nghiệm đúng bất phương trình f(x) > 0, hay a là nghiệm của bất phương trình.

Tập nghiệm S của bất phương trình

- Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm hay lời giải của bất phương trình, đôi khi nó cũng được gọi là miền đúng của bất phương trình.

Trong nhiều tài liệu người ta cũng gọi tập nghiệm của bất phương trình là nghiệm của bất phương trình.

Ví dụ Bất phương trình 4.x + 2 > 0 nghiệm đúng với mọi số thực x > -0.5. Tập nghiệm của bất phương trình là { x ∈ R | x > -0.5 } = (0.5; $\infty$ $\infty$)

Phân loại bất phương trình:

Các bất phương trình đại số bậc k là các bất phương trình trong đó f(x) là đa thức bậc k.
Các bất phương trình vô tỷ là các bất phương trình có chứa phép khai căn
Các bất phương trình mũ là các bất phương trình có chứa hàm mũ (chứa biến trên lũy thừa.
Các bất phương trình logarit là các bất phương trình có chứa hàm logarit (chứa biến trong dấu logarit).

2. Cách xét dấu tam thức bậc hai

Xét tam thức bậc hai $y = ax^{2} + bx + c;(a \neq 0)$ $y = ax^{2} + bx + c;(a \neq 0)$

$y \geq 0\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a > 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$ $y \geq 0\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a > 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$

$y \leq 0;\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a < 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$ $y \leq 0;\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a < 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$

3. Cách giải bất phương trình

Các dạng bất phương trình chứa căn

Dạng 1: Bất phương trình có dạng: $\sqrt{f(x)} < g(x) \Leftrightarrow \left\{ \begin{matrix} g(x) > 0 \\ 0 \leq f(x) < g^{2}(x) \\ \end{matrix} \right.$ $\sqrt{f(x)} < g(x) \Leftrightarrow \left\{ \begin{matrix} g(x) > 0 \\ 0 \leq f(x) < g^{2}(x) \\ \end{matrix} \right.$

Dạng 2: Bất phương trình: $\sqrt{f(x)} > g(x) \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} g(x) < 0 \\ f(x) \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} g(x) \geq 0 \\ f(x) > g^{2}(x) \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\sqrt{f(x)} > g(x) \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} g(x) < 0 \\ f(x) \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} g(x) \geq 0 \\ f(x) > g^{2}(x) \\ \end{matrix} \right.\ \\ \end{matrix} \right.$

Cách giải bất phương trình chứa căn

Khi giải bất phương trình ta sẽ làm theo các bước cơ bản sau:

Bước 1: Tìm điều kiện xác định (nếu có)

Bước 2: Sử dụng phép biến đổi tương đương chuyển bất phương trình về hệ bất phương trình đại số, từ đó xác định nghiệm x

Bước 3: kiểm tra nghiệm cùng điều kiện ở bước 1

Bước 4. Kết luận

2. Bài toán giải bất phương trình lớp 10

Bài tập 1: Tìm tập nghiệm S của bất phương trình $\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15$ $\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15$

Hướng dẫn giải

Điều kiện xác định: ${x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)$ ${x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)$

Bất phương trình tương đương: $\begin{matrix} \sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\ \end{matrix}$ $\begin{matrix} \sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\ \end{matrix}$Đặt $\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)$ $\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)$ (**)

$\begin{matrix} \left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\ \Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\ \Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\ \Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\ \Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Kết hợp với điều kiện (**) $\Rightarrow t \in \left[ {1; + \infty } \right)$ $\Rightarrow t \in \left[ {1; + \infty } \right)$

$\begin{matrix} \Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\ \Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\ \Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là $x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)$ $x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)$

Bài tập 2: Tìm tập nghiệm của bất phương trình: $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0$ $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0$

Hướng dẫn giải

Điều kiện xác định x2 – 6x + 8 ≠ 0 ⟺ x ≠ 2, x ≠ 4

$\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0$ $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0$

Lập bảng xét dấu ta có:

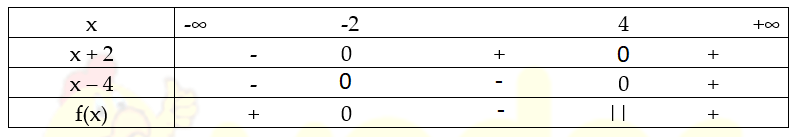
Tập nghiệm của bất phương trình

Từ bảng xét dấu ta kết luận: Tập nghiệm của bất phương trình là: x ∈ [ -2 ; 4)

Bài tập 3: Giải bất phương trình: (x2 + 3x + 1)(x2 + 3x – 3) ≥ 5 (*)

Hướng dẫn giải

Tập xác định D = $\mathbb{R}$ $\mathbb{R}$

Đặt x2 + 3x – 3 = t ⟹ x2 + 3x + 1 = t + 4

Bất phương trình (*) ⟺ t(t+4) ≥ 5

⟺ t2 + 4t – 5 ≥ 0

⟺ t ∈ (-∞; -5] ∪ [1; +∞)

$\begin{matrix} \Rightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x - 3 \leqslant - 5} \\ {{x^2} + 3x - 3 \geqslant 1} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x + 2 \leqslant 0} \\ {{x^2} + 3x - 4 \geqslant 0} \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x \in \left[ { - 2; - 1} \right]} \\ {x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)} \end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \Rightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x - 3 \leqslant - 5} \\ {{x^2} + 3x - 3 \geqslant 1} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x + 2 \leqslant 0} \\ {{x^2} + 3x - 4 \geqslant 0} \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x \in \left[ { - 2; - 1} \right]} \\ {x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)} \end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là x ∈ (-∞; -4] ∪ [1; +∞)

Bài tập 4: Giải bất phương trình: $\sqrt{5x + 1} - \sqrt{4x - 1} \leq 3\sqrt{x}$ $\sqrt{5x + 1} - \sqrt{4x - 1} \leq 3\sqrt{x}$

Hướng dẫn giải

Điều kiện xác định: $\left\{ \begin{matrix} 5x + 1 \geq 0 \\ 4x - 1 \geq 0 \\ x \geq 0 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} 5x + 1 \geq 0 \\ 4x - 1 \geq 0 \\ x \geq 0 \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \geq \dfrac{- 1}{5} \\ x \geq \dfrac{1}{4} \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow x \geq \frac{1}{4}$ $\Leftrightarrow \left\{ \begin{matrix} x \geq \dfrac{- 1}{5} \\ x \geq \dfrac{1}{4} \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow x \geq \frac{1}{4}$

Bất phương trình tương đương: $\sqrt{5x + 1} \leq 3\sqrt{x} + \sqrt{4x - 1}$ $\sqrt{5x + 1} \leq 3\sqrt{x} + \sqrt{4x - 1}$

$\Leftrightarrow 5x + 1 \leq 9x + 4x - 1 + 6\sqrt{x(4x - 1)}$ $\Leftrightarrow 5x + 1 \leq 9x + 4x - 1 + 6\sqrt{x(4x - 1)}$

$\Leftrightarrow 3\sqrt{x(4x - 1)} \geq 1 - 4x$ $\Leftrightarrow 3\sqrt{x(4x - 1)} \geq 1 - 4x$ luôn đúng với điều kiện đề bài

Vậy bất phương trình có tập nghiệm $x \geq \frac{1}{4}$ $x \geq \frac{1}{4}$

Bài tập 5: Giải bất phương trình: $\frac{1 - \sqrt{1 - 4x^{2}}}{x} < 3$ $\frac{1 - \sqrt{1 - 4x^{2}}}{x} < 3$

Hướng dẫn giải:

Điều kiện xác định: $\left\{ \begin{matrix} 1 - 4x^{2} \geq 0 \\ x \neq 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.\ \right.$ $\left\{ \begin{matrix} 1 - 4x^{2} \geq 0 \\ x \neq 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.\ \right.$

Cách 1: Sử dụng nhân liên hợp:

Bất phương trình $\Leftrightarrow \frac{(1 - \sqrt{1 - 4x^{2}})\left( 1 + \sqrt{1 - 4x^{2}} \right)}{x\left( 1 + \sqrt{1 - 4x^{2}} \right)} < 3$ $\Leftrightarrow \frac{(1 - \sqrt{1 - 4x^{2}})\left( 1 + \sqrt{1 - 4x^{2}} \right)}{x\left( 1 + \sqrt{1 - 4x^{2}} \right)} < 3$

$\Leftrightarrow 4x < 3\left( 1 + \sqrt{1 - 4x^{2}} \right)$ $\Leftrightarrow 4x < 3\left( 1 + \sqrt{1 - 4x^{2}} \right)$

$\Leftrightarrow 3\sqrt{1 - 4x^{2}} > 4x - 3 \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 4x - 3 < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4x - 3 \geq 0 \\ 9(1 - 4x^{2}) > (4x - 3)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\Leftrightarrow 3\sqrt{1 - 4x^{2}} > 4x - 3 \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 4x - 3 < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4x - 3 \geq 0 \\ 9(1 - 4x^{2}) > (4x - 3)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$

$\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x < \dfrac{3}{4} \\ x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq \dfrac{3}{4} \\ 0 < x < \dfrac{6}{13} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x < \dfrac{3}{4} \\ x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq \dfrac{3}{4} \\ 0 < x < \dfrac{6}{13} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$kết hợp điều kiện $\Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.$

Cách 2: Xét các trường hợp điều kiện:

Trường hợp 1: Với $\frac{- 1}{2} \leq x < 0$ $\frac{- 1}{2} \leq x < 0$

Ta có:

Bất phương trình $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$ $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$

$\Leftrightarrow \left\{ \begin{matrix} 1 - 3x > 0 \\ 1 - 4x^{2} < (1 - 3x)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \frac{- 1}{2} \leq x < 0$ $\Leftrightarrow \left\{ \begin{matrix} 1 - 3x > 0 \\ 1 - 4x^{2} < (1 - 3x)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \frac{- 1}{2} \leq x < 0$

Trường hợp 2: Với $0 < x \leq \frac{1}{2}$ $0 < x \leq \frac{1}{2}$

Bất phương trình $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$ $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$

$\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 1 - 3x < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 1 - 3x \geq 0 \\ 1 - 4x^{2} > (1 - 3x)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow 0 < x \leq \frac{1}{2}$ $\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 1 - 3x < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 1 - 3x \geq 0 \\ 1 - 4x^{2} > (1 - 3x)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow 0 < x \leq \frac{1}{2}$

Bài tập 6: Giải bất phương trình: $\sqrt{2\left( x^{2} - 1 \right)} \leq x + 1$ $\sqrt{2\left( x^{2} - 1 \right)} \leq x + 1$

Hướng dẫn giải

Điều kiện xác định: $x^{2} - 1 \geq 0 \Leftrightarrow x\mathbb{\in R}\backslash( - 1,1)$ $x^{2} - 1 \geq 0 \Leftrightarrow x\mathbb{\in R}\backslash( - 1,1)$

Bất phương trình $\Leftrightarrow \left\{ \begin{matrix} x + 1 \geq 0 \\ 2\left( x^{2} - 1 \right) < (x + 1)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ x \in (3, - 1) \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x + 1 \geq 0 \\ 2\left( x^{2} - 1 \right) < (x + 1)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ x \in (3, - 1) \\ \end{matrix} \right.$

Kết hợp với điều kiện đề bài $\Rightarrow x \in \lbrack 1,3)$ $\Rightarrow x \in \lbrack 1,3)$

Vậy tập nghiệm của bất phương trình là: $x \in \lbrack 1,3)$ $x \in \lbrack 1,3)$

3. Bài tập vận dụng giải bất phương trình

Bài tập 1. Giải các bất phương trình bậc hai:

a) $x^{2} - 1 \geq 0$ $x^{2} - 1 \geq 0$ b) $x^{2} - 2x - 1 < 0$ $x^{2} - 2x - 1 < 0$

c) $- 3x^{2} + 12x + 1 \leq 0$ $- 3x^{2} + 12x + 1 \leq 0$ d) $5x^{2} + x + 1 \geq 0$ $5x^{2} + x + 1 \geq 0$

Bài tập 2: Giải các bất phương trình sau:

a) $- 3x^{2} + 2x + 1 < 0$ $- 3x^{2} + 2x + 1 < 0$ b) $- 36x^{2} + 12x - 1 \geq 0$ $- 36x^{2} + 12x - 1 \geq 0$

Bài tập 3: Tìm tập xác định của hàm số: $y = \sqrt{x^{2} - 2x + 5}$ $y = \sqrt{x^{2} - 2x + 5}$

Bài tập 4. Giải bất phương trình $(x^{2} - x)^{2} + 3(x^{2} - x) + 2 \geq 0$ $(x^{2} - x)^{2} + 3(x^{2} - x) + 2 \geq 0$

Bài tập 5: Tìm tập nghiệm của các bất phương trình sau:

a) $- 3x^{2} + 2x + 1 < 0$ $- 3x^{2} + 2x + 1 < 0$

A. $S = ( - \infty; - \frac{1}{3})$ $S = ( - \infty; - \frac{1}{3})$ B. $S = (1; + \infty)$ $S = (1; + \infty)$

C. $S = \left( - \frac{1}{3};1 \right)$ $S = \left( - \frac{1}{3};1 \right)$ D. $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$ $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$

b) $x^{2} + x - 12 < 0$ $x^{2} + x - 12 < 0$

A. $S = ( - 4;3)$ B. $S = ( - \infty; - 4)$ $S = ( - \infty; - 4)$ C. $S = (3; + \infty)$ $S = (3; + \infty)$ D. $S\mathbb{= R}$ $S\mathbb{= R}$

c) $5x^{2} - 6\sqrt{5}x + 9 > 0$ $5x^{2} - 6\sqrt{5}x + 9 > 0$

A. $S\mathbb{= R}\backslash\left\{ -\frac{3\sqrt{5}}{5}\right\}$ $S\mathbb{= R}\backslash\left\{ -\frac{3\sqrt{5}}{5}\right\}$ B. $S\mathbb{= R}\backslash\left\{ \pm \frac{3\sqrt{5}}{5} \right\}$ $S\mathbb{= R}\backslash\left\{ \pm \frac{3\sqrt{5}}{5} \right\}$ C. $S\mathbb{= R}\backslash\left\{ \frac{3\sqrt{5}}{5} \right\}$ $S\mathbb{= R}\backslash\left\{ \frac{3\sqrt{5}}{5} \right\}$ D. $S=\mathbb{R}$ $S=\mathbb{R}$

d) $- 36x^{2} + 12x - 1 \geq 0$ $- 36x^{2} + 12x - 1 \geq 0$

A. $S = \left\{ \pm \frac{1}{6} \right\}$ $S = \left\{ \pm \frac{1}{6} \right\}$ B. $S = \left( -\infty;\frac{1 }{6} \right)$ $S = \left( -\infty;\frac{1 }{6} \right)$ C. $S = \left\{ \frac{1}{6} \right\}$ $S = \left\{ \frac{1}{6} \right\}$ D. $S = \left( \frac{1}{6}; + \infty \right)$ $S = \left( \frac{1}{6}; + \infty \right)$

Bài tập 6: Tìm tập nghiệm của các bất phương trình sau:

a) $- 2x^{2} + 3x - 1 \geq 0$ $- 2x^{2} + 3x - 1 \geq 0$

A. $T = \left( \frac{1}{2};1 \right)$ $T = \left( \frac{1}{2};1 \right)$ B. $T = \left( -\infty;\frac{1}{ 2} \right)$ $T = \left( -\infty;\frac{1}{ 2} \right)$ C. $T = \left\lbrack \frac{1}{2};1 \right\rbrack$ $T = \left\lbrack \frac{1}{2};1 \right\rbrack$ D. $T = (1; +\infty)$ $T = (1; +\infty)$

b) $\frac{1}{4}x^{2} - x + 1 \leq 0$ $\frac{1}{4}x^{2} - x + 1 \leq 0$

A. $T = \left\{ 3 \right\}$ $T = \left\{ 3 \right\}$ B. $T = \left\{ 4 \right\}$ $T = \left\{ 4 \right\}$ C. $T = (2;3)$ D. $T = \left\{ 2 \right\}$ $T = \left\{ 2 \right\}$

c) $- 2x^{2} + x - 1 \leq 0$ $- 2x^{2} + x - 1 \leq 0$.

A. $T\mathbb{= R}$ $T\mathbb{= R}$ B. $T\mathbb{= R}\backslash\left\{1 \right\}$ $T\mathbb{= R}\backslash\left\{1 \right\}$ C. $T = ( - 1; + \infty)$ $T = ( - 1; + \infty)$ D. $T\mathbb{= R}\backslash(3;7)$ $T\mathbb{= R}\backslash(3;7)$

d) $7x > 2x^{2} - 6$ $7x > 2x^{2} - 6$

A. $\left( \frac{3}{2};2 \right)$ $\left( \frac{3}{2};2 \right)$ B. $\left\lbrack \frac{3}{2};2 \right\rbrack$ $\left\lbrack \frac{3}{2};2 \right\rbrack$ C. $\left( -\infty;\frac{3}{2}\right)$ $\left( -\infty;\frac{3}{2}\right)$ D. $(2; + \infty)$ $(2; + \infty)$

e) $x^2 - 22x + 51 < 0$

A. $T = \varnothing$ $T = \varnothing$ B. $T\mathbb{= R}$ $T\mathbb{= R}$ C. $T = \left( 9;\frac{170}{3} \right)$ $T = \left( 9;\frac{170}{3} \right)$ D. $T = ( - \infty;2)$ $T = ( - \infty;2)$

f) $x^{2} + 5x + 6 \geq 0$ $x^{2} + 5x + 6 \geq 0$

A. $T = ( - \infty; - 3\rbrack \cup \lbrack - 2; + \infty)$ $T = ( - \infty; - 3\rbrack \cup \lbrack - 2; + \infty)$ B. $T = ( - \infty; - 3\rbrack$ $T = ( - \infty; - 3\rbrack$

C. $T = \lbrack - 3; - 2\rbrack$ $T = \lbrack - 3; - 2\rbrack$ D. $T = \lbrack - 2; + \infty)$ $T = \lbrack - 2; + \infty)$

Bài tập 7: Tìm tập xác định của hàm số $y = \sqrt{x^{2} - 3x + 2} + \frac{1}{\sqrt{x + 3}}$ $y = \sqrt{x^{2} - 3x + 2} + \frac{1}{\sqrt{x + 3}}$

Bài tập 8: Giải bất phương trình: $(x - 1)\left( x^{2} + 5x + 4 \right) \geq 0$ $(x - 1)\left( x^{2} + 5x + 4 \right) \geq 0$

Bài tập 9: Giải bất phương trình : $\frac{x^{2} + x - 1}{x - 2} > \frac{1}{x^{2} - x} + \frac{x^{3} - 2x}{x^{2} - 3x + 2}$ $\frac{x^{2} + x - 1}{x - 2} > \frac{1}{x^{2} - x} + \frac{x^{3} - 2x}{x^{2} - 3x + 2}$.

Bài tập 10: Giải bất phương trình: $(x^{2} - 4)(x^{2} + 2x) \leq 3(x^{2} + 4x + 4)$ $(x^{2} - 4)(x^{2} + 2x) \leq 3(x^{2} + 4x + 4)$.

Bài tập 11: Tìm tập nghiệm của các bất phương trình sau:

a) $(1 - 2x)\left( x^{2} - x - 1 \right) > 0$ $(1 - 2x)\left( x^{2} - x - 1 \right) > 0$

A. $S = \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ $S = \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ B. $S = \left(\frac{1 - \sqrt{5}}{2};\frac{1 }{2} \right)$ $S = \left(\frac{1 - \sqrt{5}}{2};\frac{1 }{2} \right)$

C. $S = \left( \frac{1 - \sqrt{5}}{2};\frac{1}{2} \right) \cup \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ $S = \left( \frac{1 - \sqrt{5}}{2};\frac{1}{2} \right) \cup \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ D. $S = \left( \frac{1}{2};\frac{1 + \sqrt{5}}{2} \right)$ $S = \left( \frac{1}{2};\frac{1 + \sqrt{5}}{2} \right)$

b) $x^{4} - 5x^{2} + 2x + 3 \leq 0$ $x^{4} - 5x^{2} + 2x + 3 \leq 0$

A. $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack$ B. $S = \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$

C. $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack \cup \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack \cup \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ D. $S = \varnothing$ $S = \varnothing$

Bài tập 12: Giải các bất phương trình :

a) $\frac{x^{2} - 1}{\left( x^{2} - 3 \right)\left( - 3x^{2} + 2x + 8 \right)} > 0$ $\frac{x^{2} - 1}{\left( x^{2} - 3 \right)\left( - 3x^{2} + 2x + 8 \right)} > 0$

A. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1)$ B. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup \left( \sqrt{3};2 \right)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup \left( \sqrt{3};2 \right)$

C. $S = ( - 1;1) \cup \left( \sqrt{3};2 \right)$ $S = ( - 1;1) \cup \left( \sqrt{3};2 \right)$ D. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1) \cup \left( \sqrt{3};2 \right)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1) \cup \left( \sqrt{3};2 \right)$

b) $x^{2} + 10 \leq \frac{2x^{2} + 1}{x^{2} - 8}$ $x^{2} + 10 \leq \frac{2x^{2} + 1}{x^{2} - 8}$

A. $S = (2\sqrt{2};3\rbrack$ $S = (2\sqrt{2};3\rbrack$ B. $S = \lbrack - 3; - 2\sqrt{2})$ $S = \lbrack - 3; - 2\sqrt{2})$

C. $S = \lbrack - 3; - 2\sqrt{2}) \cup (2\sqrt{2};3\rbrack$ $S = \lbrack - 3; - 2\sqrt{2}) \cup (2\sqrt{2};3\rbrack$ D. $S\mathbb{= R}\backslash\left\{ \pm \sqrt{8} \right\}$ $S\mathbb{= R}\backslash\left\{ \pm \sqrt{8} \right\}$

Đáp án bài tập vận dụng

Bài tập 1

a) Dễ thấy $f(x) = x^{2} - 1$ $f(x) = x^{2} - 1$ có $\Delta$ $\Delta' = 1 > 0,a = 1 > 0$ và có hai nghiệm phân biệt $x_{1} = - 1;\ x_{2} = 1$ $x_{1} = - 1;\ x_{2} = 1$.

Do đó ta có bảng xét dấu $f(x)$:

Nên bất phương trình $x^{2} - 1 \geq 0$ $x^{2} - 1 \geq 0$ có tập nghiệm là $S = ( - \infty; - 1) \cup (1; + \infty)$ $S = ( - \infty; - 1) \cup (1; + \infty)$.

b) Dễ thấy $g(x) = x^{2} - 2x - 1$ $g(x) = x^{2} - 2x - 1$ có $\Delta$ $\Delta' = 2 > 0,a = 1 > 0$ và có hai nghiệm phân biệt $x_{1} = 1 - \sqrt{2};$ $x_{1} = 1 - \sqrt{2};$ $x_{2} = 1 + \sqrt{2}$ $x_{2} = 1 + \sqrt{2}$.

Do đó ta có bảng xét dấu $g(x)$:

Nên bất phương trình $x^{2} - 2x - 1 < 0$ $x^{2} - 2x - 1 < 0$ có tập nghiệm là $S = \left( 1 - \sqrt{2};1 + \sqrt{2} \right)$ $S = \left( 1 - \sqrt{2};1 + \sqrt{2} \right)$.

c) Dễ thấy $h(x) = - 3x^{2} + 12x + 1$ $h(x) = - 3x^{2} + 12x + 1$ có $\Delta$ $\Delta' = 39 > 0,a = - 3 < 0$ và có hai nghiệm phân biệt $x_{1} = \frac{6 + \sqrt{39}}{3};$ $x_{1} = \frac{6 + \sqrt{39}}{3};$ $x_{2} = \frac{6 - \sqrt{39}}{3}$ $x_{2} = \frac{6 - \sqrt{39}}{3}$.

Do đó ta có bảng xét dấu $h(x)$:

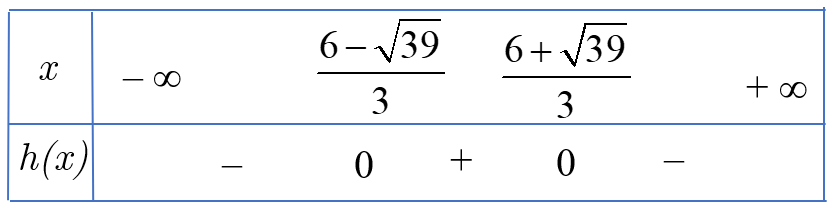
Nên bất phương trình $- 3x^{2} + 12x + 1 \leq 0$ $- 3x^{2} + 12x + 1 \leq 0$ có tập nghiệm là $S = \left( - \infty;\frac{6 - \sqrt{39}}{3} \right) \cup \left( \frac{6 + \sqrt{39}}{3}; + \infty \right)$ $S = \left( - \infty;\frac{6 - \sqrt{39}}{3} \right) \cup \left( \frac{6 + \sqrt{39}}{3}; + \infty \right)$.

d) $k(x) = 5x^{2} + x + 1$ $k(x) = 5x^{2} + x + 1$ có $\Delta = - 19 < 0$ $\Delta = - 19 < 0$ và $a = 5 > 0$ nên $k(x) > 0$ với mọi $x\mathbb{\in R}.$ $x\mathbb{\in R}.$

Từ đó suy ra bất phương trình $5x^{2} + x+ 1 \geq 0$ $5x^{2} + x+ 1 \geq 0$ có tập nghiệm là $\mathbb{R}$ $\mathbb{R}$.

Bài tập 2

a) Tam thức $f(x) = - 3x^{2} + 2x + 1$ $f(x) = - 3x^{2} + 2x + 1$ có $a = - 3 < 0$ và có hai nghiệm $x_{1} = - \frac{1}{3};$ $x_{1} = - \frac{1}{3};$ $x_{2} = 1$ $x_{2} = 1$ ($f(x)$ cùng dấu với hệ số $a$).

Suy ra $- 3x^{2} + 2x + 1 < 0 \Leftrightarrow x < - \frac{1}{3}$ $- 3x^{2} + 2x + 1 < 0 \Leftrightarrow x < - \frac{1}{3}$ hoặc $x > 1$

Vậy tập nghiệm của bất phương trình: $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$ $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$.

b) Tam thức $f(x) = - 36x^{2} + 12x - 1$ $f(x) = - 36x^{2} + 12x - 1$ có $a = - 36 < 0$ và $\Delta = 0$ $\Delta = 0$

$f(x)$ trái dấu với hệ số $a$ nên $f(x)$ âm với $\forall x \neq \frac{1}{6}$ $\forall x \neq \frac{1}{6}$ và $f\left( \frac{1}{6} \right) = 0$ $f\left( \frac{1}{6} \right) = 0$

Suy ra $- 36x^{2} + 12x - 1 \geq 0 \Leftrightarrow x = \frac{1}{6}$ $- 36x^{2} + 12x - 1 \geq 0 \Leftrightarrow x = \frac{1}{6}$

Vậy tập nghiệm của bất phương trình là $S = \left\{ \frac{1}{6} \right\}$ $S = \left\{ \frac{1}{6} \right\}$.

Bài tập 3

Điều kiện: $x^{2} - 2x + 5 \geq 0$ $x^{2} - 2x + 5 \geq 0$

Xét tam thức vế trái có $\Delta$ $\Delta' = - 4 < 0$ và $a = 1 > 0$ nên $x^{2} - 2x + 5 > 0,\ \ \forall x\mathbb{\in R}$ $x^{2} - 2x + 5 > 0,\ \ \forall x\mathbb{\in R}$.

Vậy tập xác định của hàm số $D\mathbb{= R}$ $D\mathbb{= R}$.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

--------------------------------------------------------

Bài tập công thức lượng giác lớp 10
Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12
Bất đẳng thức Cosi
Bài Tập Lượng Giác Lớp 10 cơ bản và nâng cao
35 bài tập hệ thức lượng trong tam giác có hướng dẫn
Tìm m để bất phương trình nghiệm đúng với mọi x
Tìm m để bất phương trình có nghiệm
Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn
Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn
Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn

Dạng toán tìm tập nghiệm của bất phương trình là bước đệm quan trọng để học tốt các phần tiếp theo của chương trình Toán lớp 10. Khi đã nắm chắc các quy tắc biến đổi, so sánh và biểu diễn nghiệm, bạn sẽ dễ dàng xử lý nhanh những bài toán khó hơn và đạt điểm tối đa trong các bài kiểm tra.

Hy vọng bài viết đã giúp bạn hình dung rõ ràng phương pháp giải, cách trình bày và các lỗi thường gặp cần tránh. Đừng quên luyện tập thường xuyên với các bài tập có đáp án để củng cố kỹ năng và tăng tốc độ giải.

Chúc bạn học tốt, đạt kết quả cao và luôn tự tin khi đối diện các dạng bất phương trình trong Toán lớp 10 và những lớp học tiếp theo!

Tải về Chọn file muốn tải về:

Tập nghiệm của bất phương trình

549,4 KB

Tải xuống Word
116 KB

Chia sẻ bởi: Thiên Bình

4 136.139 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất

Xóa Đăng nhập để Gửi Tìm bài trong mục này

A. CHUYÊN ĐỀ TỰ LUẬN
- Chuyên đề: Mệnh đề
  - Lý thuyết: Mệnh đề
  - Cách xác định mệnh đề, mệnh đề chứa biến
  - Cách xác định mệnh đề phủ định dễ hiểu nhất
  - Hướng dẫn cách xác định mệnh đề kéo theo và mệnh đề đảo
  - Xác định tính đúng sai của mệnh đề
  - Mệnh đề chứa kí hiệu ∀ (mọi) và ∃ (tồn tại)
  - Phát biểu mệnh đề điều kiện cần và đủ
  - Mệnh đề tương đương kèm ví dụ và bài tập
  - Phủ định mệnh đề
- Chuyên đề: Tập hợp và các phép toán trên tập hợp
  - Tập hợp
  - Các phép toán tập hợp
  - Cách xác định tập hợp
  - Các phép toán trên tập hợp
  - Giải toán bằng biểu đồ Ven
  - Bài tập ứng dụng thực tế của tập hợp Toán 10 – Có đáp án chi tiết
- Chuyên đề: Số gần đúng và sai số
  - Số gần đúng và sai số
- Chuyên đề: Hàm số bậc nhất và bậc hai
  - Lý thuyết: Hàm số
  - Hàm số y = ax + b
  - Hàm số bậc hai
    - Nhận biết hàm số bậc hai. Xác định tọa độ đỉnh, trục đối xứng của (P)
    - Cách vẽ đồ thị hàm số bậc hai và xác định chiều biến thiên (Dễ hiểu – Có ví dụ)
    - Sự tương giao của đồ thị hàm số bậc hai đầy đủ chi tiết
    - Tìm điểm cố định mà (P) luôn đi qua với mọi m
    - Tìm hàm số bậc hai thỏa điều kiện cho trước
    - Tìm GTLN, GTNN của hàm số bậc hai
    - Giải các bài toán thực tế ứng dụng hàm số bậc hai
  - Phương trình đường chuẩn của Parabol (P)
  - Tìm tập xác định của hàm số
  - Xét tính chẵn lẻ của hàm số
  - Xác định hàm số y = ax + b và sự tương giao của đồ thị hàm số
  - Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số
  - Xét sự biến thiên và vẽ đồ thị hàm số bậc nhất
  - Đồ thị hàm số chứa dấu giá trị tuyệt đối
  - Ứng dụng của hàm số bậc nhất trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
  - Xác định hàm số bậc hai
  - Đồ thị hàm số chứa dấu giá trị tuyệt đối và cho bởi nhiều công thức
  - Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
- Chuyên đề: Phương trình - Hệ phương trình
  - Đại cương về phương trình
  - Phương trình quy về phương trình bậc nhất, bậc hai
  - Phương trình và hệ phương trình bậc nhất nhiều ẩn
  - Tìm tập xác định của phương trình
  - Giải phương trình bằng phương pháp biến đổi tương đương
  - Giải và biện luận phương trình bậc nhất
  - Giải và biện luận phương trình bậc hai
  - Nghiệm của phương trình bậc hai
  - Phương trình chứa ẩn trong dấu giá trị tuyệt đối
  - Chuyên đề: Phương trình chứa ẩn ở mẫu
  - Phương trình chứa ẩn dưới dấu căn
  - Các dạng phương trình quy về phương trình bậc hai
  - Các dạng hệ phương trình đặc biệt
- Chuyên đề: Bất đẳng thức - Bất phương trình
  - Bất đẳng thức
  - Bất phương trình và hệ bất phương trình một ẩn
  - Tìm m để bất phương trình có nghiệm
  - Tìm m để bất phương trình nghiệm đúng với mọi x
  - Dấu của nhị thức bậc nhất
  - Bất phương trình bậc nhất hai ẩn
  - Dấu của tam thức bậc hai
  - Giải bất phương trình chứa căn bằng phép biến đổi tương đương
  - Giải bất phương trình chứa căn bằng cách đánh giá
  - Giải bất phương trình chứa căn bằng cách đặt ẩn phụ
  - Tập nghiệm của bất phương trình
- Chuyên đề: Thống kê
  - Bảng phân bố tần số và tần suất
  - Chuyên đề: Biểu đồ
  - Số trung bình cộng - Số trung vị - Mốt
  - Phương sai và độ lệch chuẩn
  - Hướng dẫn cách bấm máy tính Casio giải toán thống kê lớp 10
- Chuyên đề: Cung và góc lượng giác - Công thức lượng giác
  - Cung và góc lượng giác
  - Giá trị lượng giác của một cung
  - Công thức lượng giác
  - Các định nghĩa về Vecto
- Chuyên đề: Vectơ
  - Các định nghĩa về Vecto
  - Tổng và hiệu của hai vectơ
  - Tích của vectơ với một số
  - Hệ trục tọa độ
- Chuyên đề: Tích vô hướng của hai vectơ và ứng dụng
  - Giá trị lượng giác của một góc bất kì từ 0o đến 180o
- Chuyên đề Ba đường Conic
  - Phương trình Elip trong mặt phẳng tọa độ Oxy
  - Cách lập phương trình chính tắc của elip
  - Tìm tọa độ đỉnh, tiêu cự, tiêu điểm, tâm sai, trục lớn, trục nhỏ của Elip
  - Tìm M thuộc elip (E) sao cho
  - Lập phương trình chính tắc Hypebol (cách giải chi tiết)
  - Phương trình Parabol trong mặt phẳng tọa độ
  - Bài toán thực tế về ba đường Conic có đáp án
- Chuyên đề: Phương pháp tọa độ trong mặt phẳng
  - Phương trình tổng quát của đường thẳng
  - Viết phương trình đường thẳng đi qua 2 điểm
  - Cách tính Khoảng cách từ một điểm tới đường thẳng
  - Cách lập phương trình đường tròn trong mặt phẳng tọa độ (kèm ví dụ giải chi tiết)
  - Nhận dạng phương trình đường tròn, tìm tọa độ tâm và tìm bán kính
  - Vị trí tương đối của điểm với đường thẳng, đường tròn với đường tròn
  - Bộ bài tập trắc nghiệm Phương trình đường tròn cơ bản – Có đáp án
  - Bộ bài tập trắc nghiệm Viết phương trình đường tròn - Có đáp án
B. CHUYÊN ĐỀ TRẮC NGHIỆM
- Bài tập Mệnh đề, mệnh đề chứa biến có đáp án chi tiết
- Bài tập Mệnh đề phủ định Có đáp án (mức độ nhận biết)
- Bài tập Mệnh đề phủ định có đáp án (mức độ Thông hiểu)
- Bài tập Mệnh đề kéo theo, mệnh đề đảo Có đáp án
- Bài tập Mệnh đề chứa kí hiệu với mọi và tồn tại Có đáp án chi tiết
- Bài tập: Phần tử tập hợp, xác định tập hợp có đáp án
- Bài tập Toán 10 Tập hợp con có đáp án chi tiết
- Bài tập Tập hợp bằng nhau Toán 10 có đáp án chi tiết
- Bài tập tìm giao các tập hợp Toán 10 có đáp án chi tiết
- Bài tập tìm hợp các tập hợp Toán 10 có đáp án chi tiết
- Bài tập Tìm hiệu và phần bù của tập hợp – Có lời giải chi tiết
- Bài tập Tìm hiệu và phần bù của tập hợp – Có lời giải chi tiết
- Các phép toán trên tập hợp chứa tham số Có đáp án chi tiết

Lớp 10
Toán lớp 10
Chuyên đề Toán 10
Đề thi khảo sát chất lượng đầu năm lớp 10
Đề thi giữa kì 1 lớp 10
Đề thi học kì 1 lớp 10
Đề thi giữa kì 2 lớp 10
Đề thi học kì 2 lớp 10
Thi học sinh giỏi lớp 10
Đề kiểm tra 15 phút lớp 10
Toán 10 Kết nối tri thức
Toán 10 Chân trời sáng tạo
Toán 10 Cánh Diều
Lý thuyết Toán 10 KNTT
Lý thuyết Toán 10 CTST

Tham khảo thêm

Xác định Parabol y = ax^2 + bx + c
Phương trình tổng quát của đường thẳng
Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt
Tìm m để bất phương trình có nghiệm
Giải bất phương trình chứa căn bằng cách đặt ẩn phụ
Xác định vectơ chỉ phương của đường thẳng
Giải bất phương trình chứa căn bằng phép biến đổi tương đương
Tìm m để bất phương trình nghiệm đúng với mọi x
Giải bất phương trình chứa căn bằng cách đánh giá
Viết phương trình tham số, phương trình chính tắc của đường thẳng

Chuyên đề Toán 10

Xác định vectơ chỉ phương của đường thẳng
Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt
Phương trình tổng quát của đường thẳng
Bài tập tích vô hướng của hai vectơ
Viết phương trình tham số, phương trình chính tắc của đường thẳng
Xác định Parabol y = ax^2 + bx + c

Xem thêm

Gợi ý cho bạn

Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1
TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao
Được 18-20 điểm khối A1 nên đăng ký trường nào?

Xem thêm

Tập nghiệm của bất phương trình

Chỉ mua tài liệu trên 25.000đ Ưu đãi kèm thêm

Mua gói VnDoc Pro chỉ với giá

79.000đ 59.000đ

30 lượt tải tài liệu thường
10.000+ bài luyện Trắc nghiệm trực tuyến
Không quảng cáo

Mua tài liệu này và Gói Thành viên 84.000đ ×

Thông tin thanh toán nhanh

Tên tài liệu:

Tập nghiệm của bất phương trình

25.000đ

Số điện thoại/email

Vui lòng nhập số điện thoại hoặc email hợp lệ.

Tải nhanh tài liệu này 25.000đ Hỗ trợ Zalo × ← Thanh toán 25.000đ để tải tài liệu

Tên tài khoản:CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META
Số tài khoản:1038633514Copy
Ngân hàng:Vietcombank
Số tiền:25.000đ
Nội dung bắt buộc*: Copy

Ngân hàng Ngoại thương Việt Nam Chi nhánh Vietcombank Thành Công

Vui lòng giữ đúng nội dung KH khi chuyển khoản và giữ nguyên cửa sổ này để tải tài liệu tự động.

Hỗ trợ Zalo

Từ khóa » Cách Giải Bất Phương Trình Toán 10

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bất phương trình Toán 10

Tìm tập nghiệm của bất phương trình

1. Bất phương trình

Tập nghiệm S của bất phương trình

2. Cách xét dấu tam thức bậc hai

3. Cách giải bất phương trình

Cách giải bất phương trình chứa căn

2. Bài toán giải bất phương trình lớp 10

3. Bài tập vận dụng giải bất phương trình

Đáp án bài tập vận dụng

Tập nghiệm của bất phương trình

Tải xuống Word

Có thể bạn quan tâm

A. CHUYÊN ĐỀ TỰ LUẬN

B. CHUYÊN ĐỀ TRẮC NGHIỆM

Lớp 10

Toán lớp 10

Chuyên đề Toán 10

Đề thi khảo sát chất lượng đầu năm lớp 10

Đề thi giữa kì 1 lớp 10

Đề thi học kì 1 lớp 10

Đề thi giữa kì 2 lớp 10

Đề thi học kì 2 lớp 10

Thi học sinh giỏi lớp 10

Đề kiểm tra 15 phút lớp 10

Toán 10 Kết nối tri thức

Toán 10 Chân trời sáng tạo

Toán 10 Cánh Diều

Lý thuyết Toán 10 KNTT

Lý thuyết Toán 10 CTST

Tham khảo thêm

Xác định Parabol y = ax^2 + bx + c

Phương trình tổng quát của đường thẳng

Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt

Tìm m để bất phương trình có nghiệm

Giải bất phương trình chứa căn bằng cách đặt ẩn phụ

Xác định vectơ chỉ phương của đường thẳng

Giải bất phương trình chứa căn bằng phép biến đổi tương đương

Tìm m để bất phương trình nghiệm đúng với mọi x

Giải bất phương trình chứa căn bằng cách đánh giá

Viết phương trình tham số, phương trình chính tắc của đường thẳng

Chuyên đề Toán 10

Xác định vectơ chỉ phương của đường thẳng

Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt

Phương trình tổng quát của đường thẳng

Bài tập tích vô hướng của hai vectơ

Viết phương trình tham số, phương trình chính tắc của đường thẳng

Xác định Parabol y = ax^2 + bx + c

Gợi ý cho bạn

Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1

TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4

Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao

Được 18-20 điểm khối A1 nên đăng ký trường nào?