Thảo Luận - Cân Bằng Cây AVL (Code) | VN-Zoom
Có thể bạn quan tâm
Speedtest Telegram Discord VNZoom Beta 
Moderator
Thành viên BQT Cân bằng cây là việc rất cần thiết để tối ưu việc tìm kiếm và thêm xoá dễ dàng hơn. Để cân bằng cây thì cây AVL là cây dễ dàng cân bằng nhất, các bạn có thể đọc thêm phần lý thuyết để hiểu rõ hơn về cách cân bằng cây AVL trước khi bắt đầu code. Xem bài lý thuyết: https://vn-z.vn/threads/thuat-toan-can-bang-cay-avl.32451/ Chuẩn bị Cấu trúc của một node cây AVL Một node cần lưu trữ bốn thuộc tính bao gồm: 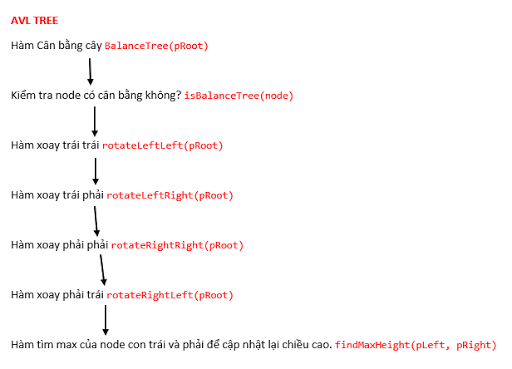 Thường thì lúc viết, mình sẽ suy luận từ trên xuống dưới để tạo ra các hàm, mục đích là để chia nhỏ vấn đề. Nhưng lúc mình code mình sẽ code từ dưới code lên. Tức là mình sẽ viết hàm findMax sau đó viết các hàm xoay cho tới hàm kiểm tra node và cuối cùng là hàm cân bằng cây. Khi viết từng hàm, mình sẽ suy nghĩ hết tất cả các trường hợp có thể xảy ra và viết như một đứa trẻ, tức là mình không ngồi đánh giá xem liệu dòng code đó có dư thừa hay không? Có hay không thì mặc kệ, việc đó để cho version 2 làm. Và tin mình đi, mình gần như debug khá ít. Lưu ý: Trong các hàm này, lúc bạn xoay cây sẽ không có vấn đề, nhưng lúc bạn cập nhật height cho node sẽ xảy ra trường hợp node chỉ có một con trái hoặc phải, dẫn tới node còn lại là null, và bạn cần phải xử lý trường hợp đó trước. Tham khảo code cân bằng cây AVL Code của hàm findMaxHeight: C++: int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } Code trên không cần giải thích quá nhiều, đơn giản nó sẽ kiểm tra hai node con xem thằng nào lớn hơn thì trả về thằng lớn hơn đó. Code hàm rotateLeftLeft: C++: //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } Vì là hàm xoay cây sẽ thay đổi ngay chính cây truyền vào, nên ở đây mình sẽ dùng tham chiếu. Bạn đừng hỏi là dùng con trỏ là trỏ vào địa chỉ rồi thì dùng tham chiếu để làm gì nha. Vì đơn giản là khi bạn dùng con trỏ nó sẽ sinh ra một con trỏ tạm trỏ vào pRoot ở trên, thì code sẽ sai ở dòng "pRoot = temp" pRoot tạm này sẽ được gán bằng temp chứ không được gán vào cây. Bạn cần lưu ý pRoot lúc này là một node con trỏ ở ngoài chứ không phải con trỏ của cây. Tới đây, chắc các bạn cũng đã hiểu tại sao truyền tham chiếu rồi, ý đồ của mình nằm ở đây. Bạn để ý vòng tròn màu đỏ, bên trái là con trỏ thuộc cây, bên phải là con trỏ ở ngoài cây. Tới lúc này bạn đọc code ở trên dễ hiểu hơn rồi đấy.
Thường thì lúc viết, mình sẽ suy luận từ trên xuống dưới để tạo ra các hàm, mục đích là để chia nhỏ vấn đề. Nhưng lúc mình code mình sẽ code từ dưới code lên. Tức là mình sẽ viết hàm findMax sau đó viết các hàm xoay cho tới hàm kiểm tra node và cuối cùng là hàm cân bằng cây. Khi viết từng hàm, mình sẽ suy nghĩ hết tất cả các trường hợp có thể xảy ra và viết như một đứa trẻ, tức là mình không ngồi đánh giá xem liệu dòng code đó có dư thừa hay không? Có hay không thì mặc kệ, việc đó để cho version 2 làm. Và tin mình đi, mình gần như debug khá ít. Lưu ý: Trong các hàm này, lúc bạn xoay cây sẽ không có vấn đề, nhưng lúc bạn cập nhật height cho node sẽ xảy ra trường hợp node chỉ có một con trái hoặc phải, dẫn tới node còn lại là null, và bạn cần phải xử lý trường hợp đó trước. Tham khảo code cân bằng cây AVL Code của hàm findMaxHeight: C++: int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } Code trên không cần giải thích quá nhiều, đơn giản nó sẽ kiểm tra hai node con xem thằng nào lớn hơn thì trả về thằng lớn hơn đó. Code hàm rotateLeftLeft: C++: //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } Vì là hàm xoay cây sẽ thay đổi ngay chính cây truyền vào, nên ở đây mình sẽ dùng tham chiếu. Bạn đừng hỏi là dùng con trỏ là trỏ vào địa chỉ rồi thì dùng tham chiếu để làm gì nha. Vì đơn giản là khi bạn dùng con trỏ nó sẽ sinh ra một con trỏ tạm trỏ vào pRoot ở trên, thì code sẽ sai ở dòng "pRoot = temp" pRoot tạm này sẽ được gán bằng temp chứ không được gán vào cây. Bạn cần lưu ý pRoot lúc này là một node con trỏ ở ngoài chứ không phải con trỏ của cây. Tới đây, chắc các bạn cũng đã hiểu tại sao truyền tham chiếu rồi, ý đồ của mình nằm ở đây. Bạn để ý vòng tròn màu đỏ, bên trái là con trỏ thuộc cây, bên phải là con trỏ ở ngoài cây. Tới lúc này bạn đọc code ở trên dễ hiểu hơn rồi đấy. 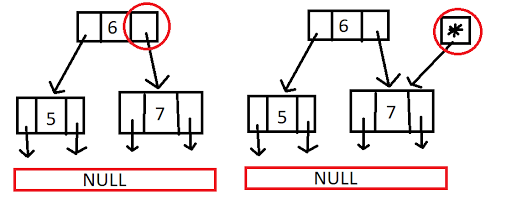 Sự khác nhau giữa truyền tham chiếu và con trỏ Code hàm rotateLeftRight: C++: void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } Bạn hiểu được các phần trên thì phần này không cần giải thích gì nữa vì nó nằm ở phần lý thuyết. Tương tự cho hai hàm bên phải vì nó đối xứng nhau. Code hàm isBalanceTree: C++: /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } Đặt tên là isBalanceTree nhưng thật ra nó kiểm tra xem node tại đó có cân bằng hay không thôi. Mà mình thấy là tên không sai, bởi vì node đang xét cân bằng thì cây con ở dưới cũng cân bằng cộng thêm việc mình duyệt cây là duyệt từ dưới lên trên. Code hàm BalanceTree: C++: //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Các bước phức tạp chủ yếu các hàm trên, hàm này chỉ đơn giản là kiểm tra xem node bị mất cân bằng ở đâu, và mất cân bằng loại gì? trái trái, trái phải, phải phải hay phải trái rồi gọi hàm xoay thôi. Nãy giờ, mình chỉ đi cân bằng cây, nhưng cây chỉ bị mất cân bằng khi thêm hoặc xoá. Vậy lúc thêm, xoá một giá trị nào đó trong cây, bạn cần cập nhật lại height của tất cả các node. C++: void Insert(NODE*& pRoot, int x) { if (pRoot == nullptr) { return; } if (x == pRoot->key) { return; } if (x > pRoot->key) { Insert(pRoot->p_right, x); if (pRoot->p_right == nullptr) { NODE* cur = createNode(x); pRoot->p_right = cur; } if (pRoot->p_left == nullptr) { pRoot->height = abs(pRoot->p_right->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } else { Insert(pRoot->p_left, x); if (pRoot->p_left == nullptr) { NODE* cur = createNode(x); pRoot->p_left = cur; } if (pRoot->p_right == nullptr) { pRoot->height = abs(pRoot->p_left->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } } Hàm Insert này mình chỉ lấy bên hàm Insert của cây bình thường chỉ thêm phần cập nhật lại height của node. Code hoàn thiện C++: struct NODE { int key; NODE* p_left; NODE* p_right; int height; }; NODE* createNode(int data) { NODE* p = new NODE; p->key = data; p->p_left = nullptr; p->p_right = nullptr; p->height = 1; return p; } int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Tổng kết Mong là bài viết dễ hiểu. Cây AVL là khởi đầu của các loại cây sau này như cây đỏ đen, cây AA các bạn tìm hiểu kỹ và tự code thử trước khi tham khảo bài viết. Mình sử dụng văn nói để dễ truyền đạt và dễ hiểu nên có thể từ ngữ sẽ không chuẩn 100%. Bạn có thể sử dụng trang web này để kiểm tra bản thân code đúng hay sai. Giả lập AVL tree Sửa lần cuối: 10/12/20 Bạn chỉ nhìn thấy những gì bạn muốn thấy. Bạn chỉ nhìn thấy những gì tôi muốn cho bạn thấy.
Sự khác nhau giữa truyền tham chiếu và con trỏ Code hàm rotateLeftRight: C++: void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } Bạn hiểu được các phần trên thì phần này không cần giải thích gì nữa vì nó nằm ở phần lý thuyết. Tương tự cho hai hàm bên phải vì nó đối xứng nhau. Code hàm isBalanceTree: C++: /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } Đặt tên là isBalanceTree nhưng thật ra nó kiểm tra xem node tại đó có cân bằng hay không thôi. Mà mình thấy là tên không sai, bởi vì node đang xét cân bằng thì cây con ở dưới cũng cân bằng cộng thêm việc mình duyệt cây là duyệt từ dưới lên trên. Code hàm BalanceTree: C++: //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Các bước phức tạp chủ yếu các hàm trên, hàm này chỉ đơn giản là kiểm tra xem node bị mất cân bằng ở đâu, và mất cân bằng loại gì? trái trái, trái phải, phải phải hay phải trái rồi gọi hàm xoay thôi. Nãy giờ, mình chỉ đi cân bằng cây, nhưng cây chỉ bị mất cân bằng khi thêm hoặc xoá. Vậy lúc thêm, xoá một giá trị nào đó trong cây, bạn cần cập nhật lại height của tất cả các node. C++: void Insert(NODE*& pRoot, int x) { if (pRoot == nullptr) { return; } if (x == pRoot->key) { return; } if (x > pRoot->key) { Insert(pRoot->p_right, x); if (pRoot->p_right == nullptr) { NODE* cur = createNode(x); pRoot->p_right = cur; } if (pRoot->p_left == nullptr) { pRoot->height = abs(pRoot->p_right->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } else { Insert(pRoot->p_left, x); if (pRoot->p_left == nullptr) { NODE* cur = createNode(x); pRoot->p_left = cur; } if (pRoot->p_right == nullptr) { pRoot->height = abs(pRoot->p_left->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } } Hàm Insert này mình chỉ lấy bên hàm Insert của cây bình thường chỉ thêm phần cập nhật lại height của node. Code hoàn thiện C++: struct NODE { int key; NODE* p_left; NODE* p_right; int height; }; NODE* createNode(int data) { NODE* p = new NODE; p->key = data; p->p_left = nullptr; p->p_right = nullptr; p->height = 1; return p; } int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Tổng kết Mong là bài viết dễ hiểu. Cây AVL là khởi đầu của các loại cây sau này như cây đỏ đen, cây AA các bạn tìm hiểu kỹ và tự code thử trước khi tham khảo bài viết. Mình sử dụng văn nói để dễ truyền đạt và dễ hiểu nên có thể từ ngữ sẽ không chuẩn 100%. Bạn có thể sử dụng trang web này để kiểm tra bản thân code đúng hay sai. Giả lập AVL tree Sửa lần cuối: 10/12/20 Bạn chỉ nhìn thấy những gì bạn muốn thấy. Bạn chỉ nhìn thấy những gì tôi muốn cho bạn thấy. 
Gà con
ủa cái xoay trái trái là sao v ạ, em xem ko hiểu S Moderator
Thành viên BQT 
 vn-z.vn You must log in or register to reply here. Chia sẻ: Facebook X (Twitter) Reddit Pinterest Tumblr WhatsApp Email Chia sẻ Link
vn-z.vn You must log in or register to reply here. Chia sẻ: Facebook X (Twitter) Reddit Pinterest Tumblr WhatsApp Email Chia sẻ Link 

- DIỄN ĐÀN Kiến Thức Công Nghệ Khoa Học Mới Reviews Công Nghệ Công Nghệ AI Tin Học Căn Bản Phần Cứng Phần Mềm Kiến thức điện tử - Tiêu Dùng Khoa Học & Công Nghệ Anti Virus Bảo Mật Lập Trình Thiết Kế WEB - VPS HOST- MẠNG Digital Marketing Kho Tài Nguyên - Học Tập Hệ điều hành Windows Windows 12 Windows 11 Windows 10 Windows 8 Hệ Điều Hành Linux Hệ Điều Hành Mac (Apple) Ghost/ WinPE - Hirent's Boot Điện Ảnh Âm Nhạc Tranh Ảnh Đọc Truyện Thể Thao Chuyện Trò Linh Tinh Điện Thoại Di Động - Thiết Bị Cầm Tay Hệ Điều Hành Android iOS (Apple) Thế Giới Thiết Bị Số Máy Ảnh Số Thiết bị hình ảnh - Truyền Hình Tin Tức Ô Tô Xe Máy Xe điện Hỏi Đáp Ô TÔ - Xe Máy Game PC & Console Thông tin Game Game Mobile 2048 Trung Tâm Thương Mại Điện Tử Telegram VN-Zoom Discord VN-Zoom Chăn Nuôi Trồng trọt
- ĐÁNH GIÁ
- BÀI MỚI
- WINDOWS
- CÔNG NGHỆ AI
Tìm kiếm
Everywhere Chủ đề This forum This thread Tìm kiếm dựa vào tiêu đề (tích để chọn) Tìm kiếm Tìm kiếm nâng cao…- Kiến Thức Công Nghệ Khoa Học Mới
- Reviews Công Nghệ
- Công Nghệ AI
- Tin Học Căn Bản
- Phần Cứng
- Phần Mềm
- Kiến thức điện tử - Tiêu Dùng
- Khoa Học & Công Nghệ
- Anti Virus
- Bảo Mật
- Lập Trình
- Thiết Kế WEB - VPS HOST- MẠNG
- Digital Marketing
- Kho Tài Nguyên - Học Tập
- Hệ điều hành Windows Windows 12 Windows 11 Windows 10 Windows 8
- Hệ Điều Hành Linux
- Hệ Điều Hành Mac (Apple)
- Ghost/ WinPE - Hirent's Boot
- Điện Ảnh
- Âm Nhạc
- Tranh Ảnh
- Đọc Truyện
- Thể Thao
- Chuyện Trò Linh Tinh
- Điện Thoại Di Động - Thiết Bị Cầm Tay Hệ Điều Hành Android iOS (Apple)
- Thế Giới Thiết Bị Số Máy Ảnh Số Thiết bị hình ảnh - Truyền Hình
- Tin Tức Ô Tô Xe Máy
- Xe điện
- Hỏi Đáp Ô TÔ - Xe Máy
- Game PC & Console
- Thông tin Game
- Game Mobile
- 2048
- Trung Tâm Thương Mại Điện Tử
- Telegram VN-Zoom
- Discord VN-Zoom
- Chăn Nuôi
- Trồng trọt
- 🔥 WINXDVD 2025 CHRISTMAS CALENDAR tặng 25 phần mềm bản quyền miễn phí với tổng giá trị 1.095 USD 🔥
We've detected that you are using AdBlock Plus or some other adblocking software which is preventing the page from fully loading.
We need money to operate the site, and almost all of it comes from our online advertising.
Please add vn-z.vn to your ad blocking whitelist or disable your adblocking software.
All the knowledge we share is completely free. If you are willing, please support us here.
×- DIỄN ĐÀN
- Thư viện Tin Học
- Lập Trình
- Thread starter statistics
- Ngày gửi 10/12/20
statistics
Moderator
Thành viên BQT Cân bằng cây là việc rất cần thiết để tối ưu việc tìm kiếm và thêm xoá dễ dàng hơn. Để cân bằng cây thì cây AVL là cây dễ dàng cân bằng nhất, các bạn có thể đọc thêm phần lý thuyết để hiểu rõ hơn về cách cân bằng cây AVL trước khi bắt đầu code. Xem bài lý thuyết: https://vn-z.vn/threads/thuat-toan-can-bang-cay-avl.32451/ Chuẩn bị Cấu trúc của một node cây AVL Một node cần lưu trữ bốn thuộc tính bao gồm: - key: Để lưu giá trị của Node.
- p_left: lưu con trỏ trỏ tới bên trái.
- p_right: lưu con trỏ trỏ tới bên phải.
- height: lưu chiều cao của node.
- Tất cả các node lá hoặc node mới chưa thêm vào trong cây có height = 1.
- Một node bất kì có chiều cao (height) là max(pLeft, pRight) + 1 tức là chiều cao lớn nhất của node bên trái hoặc bên phải và cộng thêm một đơn vị.
- Một vị trí được cho là mất cân bằng khi height node bên phải và node bên trái chênh lệch nhau từ hai đơn vị trở lên.
- Khi kiểm tra cây có cân bằng hay không, quy ước: -1 là cây lệch trái, 0 là cây cân bằng, 1 là cây lệch bên phải của node đó.
- Mỗi khi thêm hoặc xoá phần tử ta cần cập nhật lại chiều cao của cây.
- Để có thể dễ dàng duyệt, trong phần code mình sẽ sử dụng phép duyệt LRN để duyệt từ cuối cây duyệt lên.
 Thường thì lúc viết, mình sẽ suy luận từ trên xuống dưới để tạo ra các hàm, mục đích là để chia nhỏ vấn đề. Nhưng lúc mình code mình sẽ code từ dưới code lên. Tức là mình sẽ viết hàm findMax sau đó viết các hàm xoay cho tới hàm kiểm tra node và cuối cùng là hàm cân bằng cây. Khi viết từng hàm, mình sẽ suy nghĩ hết tất cả các trường hợp có thể xảy ra và viết như một đứa trẻ, tức là mình không ngồi đánh giá xem liệu dòng code đó có dư thừa hay không? Có hay không thì mặc kệ, việc đó để cho version 2 làm. Và tin mình đi, mình gần như debug khá ít. Lưu ý: Trong các hàm này, lúc bạn xoay cây sẽ không có vấn đề, nhưng lúc bạn cập nhật height cho node sẽ xảy ra trường hợp node chỉ có một con trái hoặc phải, dẫn tới node còn lại là null, và bạn cần phải xử lý trường hợp đó trước. Tham khảo code cân bằng cây AVL Code của hàm findMaxHeight: C++: int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } Code trên không cần giải thích quá nhiều, đơn giản nó sẽ kiểm tra hai node con xem thằng nào lớn hơn thì trả về thằng lớn hơn đó. Code hàm rotateLeftLeft: C++: //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } Vì là hàm xoay cây sẽ thay đổi ngay chính cây truyền vào, nên ở đây mình sẽ dùng tham chiếu. Bạn đừng hỏi là dùng con trỏ là trỏ vào địa chỉ rồi thì dùng tham chiếu để làm gì nha. Vì đơn giản là khi bạn dùng con trỏ nó sẽ sinh ra một con trỏ tạm trỏ vào pRoot ở trên, thì code sẽ sai ở dòng "pRoot = temp" pRoot tạm này sẽ được gán bằng temp chứ không được gán vào cây. Bạn cần lưu ý pRoot lúc này là một node con trỏ ở ngoài chứ không phải con trỏ của cây. Tới đây, chắc các bạn cũng đã hiểu tại sao truyền tham chiếu rồi, ý đồ của mình nằm ở đây. Bạn để ý vòng tròn màu đỏ, bên trái là con trỏ thuộc cây, bên phải là con trỏ ở ngoài cây. Tới lúc này bạn đọc code ở trên dễ hiểu hơn rồi đấy.
Thường thì lúc viết, mình sẽ suy luận từ trên xuống dưới để tạo ra các hàm, mục đích là để chia nhỏ vấn đề. Nhưng lúc mình code mình sẽ code từ dưới code lên. Tức là mình sẽ viết hàm findMax sau đó viết các hàm xoay cho tới hàm kiểm tra node và cuối cùng là hàm cân bằng cây. Khi viết từng hàm, mình sẽ suy nghĩ hết tất cả các trường hợp có thể xảy ra và viết như một đứa trẻ, tức là mình không ngồi đánh giá xem liệu dòng code đó có dư thừa hay không? Có hay không thì mặc kệ, việc đó để cho version 2 làm. Và tin mình đi, mình gần như debug khá ít. Lưu ý: Trong các hàm này, lúc bạn xoay cây sẽ không có vấn đề, nhưng lúc bạn cập nhật height cho node sẽ xảy ra trường hợp node chỉ có một con trái hoặc phải, dẫn tới node còn lại là null, và bạn cần phải xử lý trường hợp đó trước. Tham khảo code cân bằng cây AVL Code của hàm findMaxHeight: C++: int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } Code trên không cần giải thích quá nhiều, đơn giản nó sẽ kiểm tra hai node con xem thằng nào lớn hơn thì trả về thằng lớn hơn đó. Code hàm rotateLeftLeft: C++: //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } Vì là hàm xoay cây sẽ thay đổi ngay chính cây truyền vào, nên ở đây mình sẽ dùng tham chiếu. Bạn đừng hỏi là dùng con trỏ là trỏ vào địa chỉ rồi thì dùng tham chiếu để làm gì nha. Vì đơn giản là khi bạn dùng con trỏ nó sẽ sinh ra một con trỏ tạm trỏ vào pRoot ở trên, thì code sẽ sai ở dòng "pRoot = temp" pRoot tạm này sẽ được gán bằng temp chứ không được gán vào cây. Bạn cần lưu ý pRoot lúc này là một node con trỏ ở ngoài chứ không phải con trỏ của cây. Tới đây, chắc các bạn cũng đã hiểu tại sao truyền tham chiếu rồi, ý đồ của mình nằm ở đây. Bạn để ý vòng tròn màu đỏ, bên trái là con trỏ thuộc cây, bên phải là con trỏ ở ngoài cây. Tới lúc này bạn đọc code ở trên dễ hiểu hơn rồi đấy.  Sự khác nhau giữa truyền tham chiếu và con trỏ Code hàm rotateLeftRight: C++: void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } Bạn hiểu được các phần trên thì phần này không cần giải thích gì nữa vì nó nằm ở phần lý thuyết. Tương tự cho hai hàm bên phải vì nó đối xứng nhau. Code hàm isBalanceTree: C++: /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } Đặt tên là isBalanceTree nhưng thật ra nó kiểm tra xem node tại đó có cân bằng hay không thôi. Mà mình thấy là tên không sai, bởi vì node đang xét cân bằng thì cây con ở dưới cũng cân bằng cộng thêm việc mình duyệt cây là duyệt từ dưới lên trên. Code hàm BalanceTree: C++: //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Các bước phức tạp chủ yếu các hàm trên, hàm này chỉ đơn giản là kiểm tra xem node bị mất cân bằng ở đâu, và mất cân bằng loại gì? trái trái, trái phải, phải phải hay phải trái rồi gọi hàm xoay thôi. Nãy giờ, mình chỉ đi cân bằng cây, nhưng cây chỉ bị mất cân bằng khi thêm hoặc xoá. Vậy lúc thêm, xoá một giá trị nào đó trong cây, bạn cần cập nhật lại height của tất cả các node. C++: void Insert(NODE*& pRoot, int x) { if (pRoot == nullptr) { return; } if (x == pRoot->key) { return; } if (x > pRoot->key) { Insert(pRoot->p_right, x); if (pRoot->p_right == nullptr) { NODE* cur = createNode(x); pRoot->p_right = cur; } if (pRoot->p_left == nullptr) { pRoot->height = abs(pRoot->p_right->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } else { Insert(pRoot->p_left, x); if (pRoot->p_left == nullptr) { NODE* cur = createNode(x); pRoot->p_left = cur; } if (pRoot->p_right == nullptr) { pRoot->height = abs(pRoot->p_left->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } } Hàm Insert này mình chỉ lấy bên hàm Insert của cây bình thường chỉ thêm phần cập nhật lại height của node. Code hoàn thiện C++: struct NODE { int key; NODE* p_left; NODE* p_right; int height; }; NODE* createNode(int data) { NODE* p = new NODE; p->key = data; p->p_left = nullptr; p->p_right = nullptr; p->height = 1; return p; } int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Tổng kết Mong là bài viết dễ hiểu. Cây AVL là khởi đầu của các loại cây sau này như cây đỏ đen, cây AA các bạn tìm hiểu kỹ và tự code thử trước khi tham khảo bài viết. Mình sử dụng văn nói để dễ truyền đạt và dễ hiểu nên có thể từ ngữ sẽ không chuẩn 100%. Bạn có thể sử dụng trang web này để kiểm tra bản thân code đúng hay sai. Giả lập AVL tree Sửa lần cuối: 10/12/20 Bạn chỉ nhìn thấy những gì bạn muốn thấy. Bạn chỉ nhìn thấy những gì tôi muốn cho bạn thấy.
Sự khác nhau giữa truyền tham chiếu và con trỏ Code hàm rotateLeftRight: C++: void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } Bạn hiểu được các phần trên thì phần này không cần giải thích gì nữa vì nó nằm ở phần lý thuyết. Tương tự cho hai hàm bên phải vì nó đối xứng nhau. Code hàm isBalanceTree: C++: /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như height bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } Đặt tên là isBalanceTree nhưng thật ra nó kiểm tra xem node tại đó có cân bằng hay không thôi. Mà mình thấy là tên không sai, bởi vì node đang xét cân bằng thì cây con ở dưới cũng cân bằng cộng thêm việc mình duyệt cây là duyệt từ dưới lên trên. Code hàm BalanceTree: C++: //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Các bước phức tạp chủ yếu các hàm trên, hàm này chỉ đơn giản là kiểm tra xem node bị mất cân bằng ở đâu, và mất cân bằng loại gì? trái trái, trái phải, phải phải hay phải trái rồi gọi hàm xoay thôi. Nãy giờ, mình chỉ đi cân bằng cây, nhưng cây chỉ bị mất cân bằng khi thêm hoặc xoá. Vậy lúc thêm, xoá một giá trị nào đó trong cây, bạn cần cập nhật lại height của tất cả các node. C++: void Insert(NODE*& pRoot, int x) { if (pRoot == nullptr) { return; } if (x == pRoot->key) { return; } if (x > pRoot->key) { Insert(pRoot->p_right, x); if (pRoot->p_right == nullptr) { NODE* cur = createNode(x); pRoot->p_right = cur; } if (pRoot->p_left == nullptr) { pRoot->height = abs(pRoot->p_right->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } else { Insert(pRoot->p_left, x); if (pRoot->p_left == nullptr) { NODE* cur = createNode(x); pRoot->p_left = cur; } if (pRoot->p_right == nullptr) { pRoot->height = abs(pRoot->p_left->height) + 1; } else { pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } } } Hàm Insert này mình chỉ lấy bên hàm Insert của cây bình thường chỉ thêm phần cập nhật lại height của node. Code hoàn thiện C++: struct NODE { int key; NODE* p_left; NODE* p_right; int height; }; NODE* createNode(int data) { NODE* p = new NODE; p->key = data; p->p_left = nullptr; p->p_right = nullptr; p->height = 1; return p; } int findMaxHeight(NODE* pLeft, NODE* pRight) { if (pLeft == nullptr) return pRight->height; else if (pRight == nullptr) return pLeft->height; return pLeft->height > pRight->height ? pLeft->height : pRight->height; } /*Check Tree is Balance*/ int isBalanceTree(NODE* pRoot) { if (pRoot == nullptr || pRoot->p_left == nullptr && pRoot->p_right == nullptr) { // trái phải đều null return 0; // can bang } else if (pRoot->p_left == nullptr ) { // trái null phải không null if (pRoot->p_right->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return 1; else return 0; } else if (pRoot->p_right == nullptr) { // phải null trái không null if (pRoot->p_left->height > 1) // lệch nhau 2 đơn vị, vì null thì xem như bậc bằng 0 return -1; else return 0; } int check = pRoot->p_right->height - pRoot->p_left->height; if (check >= 2) { // lệch nhau 2 đơn vị mà dương return 1; // lech phai } else if (check <= -2) { // lệch nhau 2 đơn vị mà âm return -1; // lech trai } else return 0; } //Xoay trai void rotateLeftLeft(NODE* &pRoot) { NODE* temp = pRoot->p_left; // giu P1 pRoot->p_left = pRoot->p_left->p_right; // bán con temp->p_right = pRoot; // Xoay pRoot = temp;// P1 lên làm cha //Cap nhat height. Cần xác định là những node lá sẽ không thay đổi height nên ta chỉ cập nhật các node không phải lá NODE* pNow = pRoot->p_right; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; pRoot->height = findMaxHeight(pRoot->p_left, pRoot->p_right) + 1; } void rotateLeftRight(NODE*& pRoot) { NODE* pCur = pRoot->p_left; // pCur giữ vị trí P1 để thực hiện quay trái trước, pCur lúc này đóng vai trò là pRoot của cây con nhỏ pRoot->left pRoot->p_left = pCur->p_right; pCur->p_right = nullptr; pRoot->p_left->p_left = pCur; //Cập nhật height cho cây sau khi xoay . NODE* pNow = pRoot->p_left; NODE* pNow1 = pNow->p_left; pNow1->height = findMaxHeight(pNow1->p_left, pNow1->p_right) + 1; pNow->height = findMaxHeight(pNow->p_left, pNow->p_right) + 1; //Thực hiện xong công việc quay trái, bây giờ thực hiện công việc quay phải //Cây hiện tại đã biến thành cây lệch trái bên trái => gọi hàm cũ là xong. rotateLeftLeft(pRoot); } //Balance AVL /*Bool is check succesfull*/ bool BalanceTree(NODE* &pRoot) { if (pRoot == nullptr) { return 0; } BalanceTree(pRoot->p_left); BalanceTree(pRoot->p_right); if (isBalanceTree(pRoot) == -1) { // lech trai NODE* p1 = pRoot->p_left; int index = p1->p_right->height - p1->p_left->height; if (index <= 0) { rotateLeftLeft(pRoot); } else { rotateLeftRight(pRoot); } } else if ( isBalanceTree(pRoot) == 1 ) { // lech phai NODE* p1 = pRoot->p_right; int index = p1->p_right->height - p1->p_left->height; if (index >= 0) { rotateRightRight(pRoot); } else { rotateRightLeft(pRoot); } } } Tổng kết Mong là bài viết dễ hiểu. Cây AVL là khởi đầu của các loại cây sau này như cây đỏ đen, cây AA các bạn tìm hiểu kỹ và tự code thử trước khi tham khảo bài viết. Mình sử dụng văn nói để dễ truyền đạt và dễ hiểu nên có thể từ ngữ sẽ không chuẩn 100%. Bạn có thể sử dụng trang web này để kiểm tra bản thân code đúng hay sai. Giả lập AVL tree Sửa lần cuối: 10/12/20 Bạn chỉ nhìn thấy những gì bạn muốn thấy. Bạn chỉ nhìn thấy những gì tôi muốn cho bạn thấy. Chủ đề tương tự
Đưa website của bạn lên Internet trong vòng nửa nốt nhạc Đóng gói cài đặt kèm database trên Visual Studio 2019 Đóng gói cài đặt kèm database trên Visual Studio 2015 Đọc Nhiều File Excel Cùng Cấu Trúc Vào Gridview Đây có phải là mã nguồn Facebook từ 2003simpboy
Gà con
ủa cái xoay trái trái là sao v ạ, em xem ko hiểu S statistics
Moderator
Thành viên BQT simpboy nói: ủa cái xoay trái trái là sao v ạ, em xem ko hiểu Nhấn để mở rộng...
simpboy nói: ủa cái xoay trái trái là sao v ạ, em xem ko hiểu Nhấn để mở rộng...bạn xem bài lý thuyết này nha, nó sẽ giải thích kỹ á.

Thuật toán cân bằng cây AVL
Tại sao phải cân bằng cây? Cân bằng cây là gì? Cách cân bằng cây AVL như thế nào? Trong bài viết này mình sẽ trình bày lý thuyết, bài viết sau mình sẽ trình bày code và giải thích. Ngoài ra các bạn nên tìm hiểu thêm các cách cân bằng cây khác nữa. Tại sao phải cân bằng cây? Bạn hãy nhìn vào...ĐANG THẢO LUẬN
- JEDEC xây dựng tiêu chuẩn bộ nhớ hoàn toàn mới SPHBM4: vượt trội DDR5/GDDR7, tiệm cận HBM4 lúc 16:22 Xin hướng dẫn backup key ESET Internet Security lúc 11:37 Tạo một trang web miễn phí lúc 08:36 Hogwarts Legacy: Siêu phẩm nhập vai thế giới phép thuật trị giá hơn 1,2 triệu đồng đang được tặng miễn phí lúc 08:30 Hôm qua Nga công bố bộ xử lý Irtysh dựa trên kiến trúc LoongArch, hướng tới máy chủ và PC, tối đa 64 nhân, xung nhịp 2.0GHz lúc 08:18 Hôm qua Chuẩn kết nối GPMI do Trung Quốc tự phát triển sắp ra mắt, tham vọng vượt Type-C và HDMI lúc 08:23, Thứ sáu Atlas Data Storage ra mắt ổ cứng DNA đầu tiên trên thế giới! Mật độ lưu trữ cao hơn HDD 1000 lần, tuổi thọ lên tới hàng nghìn năm lúc 08:27, Thứ hai
ĐỪNG BÕ LỠ
- JEDEC xây dựng tiêu chuẩn bộ nhớ hoàn toàn mới SPHBM4: vượt trội DDR5/GDDR7, tiệm cận HBM4 lúc 16:22 Xin hướng dẫn backup key ESET Internet Security lúc 11:37 Tạo một trang web miễn phí lúc 08:36 SEA Games 33 ngày 13.12: Việt Nam bước vào ngày thi đấu then chốt, nhiều nội dung chung kết tranh huy chương vàng. lúc 09:02 Hôm qua Hogwarts Legacy: Siêu phẩm nhập vai thế giới phép thuật trị giá hơn 1,2 triệu đồng đang được tặng miễn phí lúc 08:30 Hôm qua
Bài Viết Mới
-
JEDEC xây dựng tiêu chuẩn bộ nhớ hoàn toàn mới SPHBM4: vượt trội DDR5/GDDR7, tiệm cận HBM4
- Started by VNZ-NEWS
- lúc 16:22
- Trả lời: 1
-
Nhờ tư vấnXin hướng dẫn backup key ESET Internet Security
- Started by qminh19
- lúc 11:37
- Trả lời: 2
-
Hỏi/ Thắc mắcTạo một trang web miễn phí
- Started by taihdhpu2
- lúc 08:36
- Trả lời: 1
-
SEA Games 33 ngày 13.12: Việt Nam bước vào ngày thi đấu then chốt, nhiều nội dung chung kết tranh huy chương vàng.
- Started by VNZ-NEWS
- lúc 09:02 Hôm qua
- Trả lời: 0
-
Hogwarts Legacy: Siêu phẩm nhập vai thế giới phép thuật trị giá hơn 1,2 triệu đồng đang được tặng miễn phí
- Started by VNZ-NEWS
- lúc 08:30 Hôm qua
- Trả lời: 1
- DIỄN ĐÀN
- Thư viện Tin Học
- Lập Trình
Từ khóa » Cách Cân Bằng Cây Avl
-
Cây AVL Và Các Thao Tác - TEK4
-
Cây AVL Trong Cấu Trúc Dữ Liệu Và Giải Thuật
-
Chi Tiết Bài Học Cây Cân Bằng - Vimentor
-
Cây AVL (AVL Tree) - Phần 1 (Insertion)
-
[PDF] CÂY CÂN BẰNG AVL
-
[Basic-DSAA] Cấu Trúc Dữ Liệu Cây - Cây AVL. - CodeLearn
-
Cấu Trúc Dữ Liệu Cây Cân Bằng - Cửu Dương Thần Công . Com
-
CTDL>: 9.Cấu Trúc Cây (tiếp) - Cây Cân Bằng AVL - YouTube
-
1.CÂY NHỊ PHÂN CÂN BẰNG HOÀN TOÀN
-
Cây AVL (AVL Tree) – Phần 2 (Deletion)
-
Thuật Toán Cân Bằng Cây AVL | VN-Zoom