Thuật Toán Quay Lui Và Minh Họa - O₂ Education

Trang chủ » Thuật Toán đệ Quy Quay Lui Trong Java » Thuật Toán Quay Lui Và Minh Họa - O₂ Education

Có thể bạn quan tâm

Thuật toán quay lui và minh họa

1. Thuật toán quay lui là gì?

Thuật toán quay lui (Backtracking) là một kĩ thuật thiết kế giải thuật dựa trên đệ quy. Ý tưởng của quay lui là tìm lời giải từng bước, mỗi bước chọn một trong số các lựa chọn khả dĩ và đệ quy. Người đầu tiên đề ra thuật ngữ này (backtrack) là nhà toán học người Mỹ D. H. Lehmer vào những năm 1950.

2. Thuật toán quay lui sử dụng khi nào?

Thuật toán quay lui thường được sử dụng để giải bài toán liệt kê các cấu hình (như bài toán sinh các xâu nhị phân). Mỗi cấu hình được xây dựng bằng cách xác định từng phần tử. Mỗi phần tử lại được chọn bằng cách thử tất cả các khả năng. Các bước trong việc liệt kê cấu hình dạng X[1…n]:
  • Xét tất cả các giá trị X[1] có thể nhận, thử X[1] nhận các giá trị đó. Với mỗi giá trị của X[1] ta sẽ:
  • Xét tất cả giá trị X[2] có thể nhận, lại thử X[2] cho các giá trị đó. Với mỗi giá trị X[2] lại xét khả năng giá trị của X[3]…tiếp tục như vậy cho tới bước:
  • …
  • Xét tất cả giá trị X[n] có thể nhận, thử cho X[n] nhận lần lượt giá trị đó.
  • Thông báo cấu hình tìm được.

Để cài đặt thuật toán quay lui, chúng ta sử dụng một chương trình con (hàm function, thủ tục procedure) và gọi đến hàm đó trong chương trình chính của mình. Mô hình của thuật toán quay lui sử dụng ngôn ngữ Python như sau:

def quay_lui(i): for j in [tập_các_phương_án_x[i] có thể nhận]: <thử đặt x[i] = j> if <x[i] là phần tử cuối cùng trong cấu hình>: <thông báo cấu hình> else: <ghi nhận việc cho x[i] nhận giá trị j nếu cần> <gọi đệ quy đến quay_lui(i+1)> <bỏ ghi nhận việc cho x[i] nhận giá trị j để thử giá trị khác nếu cần>

Thuật toán quay lui sẽ bắt đầu bằng lời gọi quay_lui(1)

3. Minh họa của thuật toán quay lui (Backtracking)

3.1. Sử dụng thuật toán quay lui để sinh các dãy nhị phân độ dài n

Dưới đây, chúng ta cùng xem mã chương trình sinh các dãy nhị phân có độ dài n bằng cách sử dụng thuật toán quay lui.

n = 3 x = n*[0] def fine_print(x): tmp = '' for i in x: tmp += str(i) return tmp def bin_gen(i): for j in range(0,3): x[i] = j if i == n-1: print(fine_print(x)) else: bin_gen(i+1) bin_gen(0)

Các giải khác bằng cách sử dụng vòng lặp, xin mời bạn đọc xem tại đây Thuật toán sinh các dãy nhị phân có độ dài n

3.2. Sử dụng backtracking để giải Sudoku

thuật toán giải sudoku

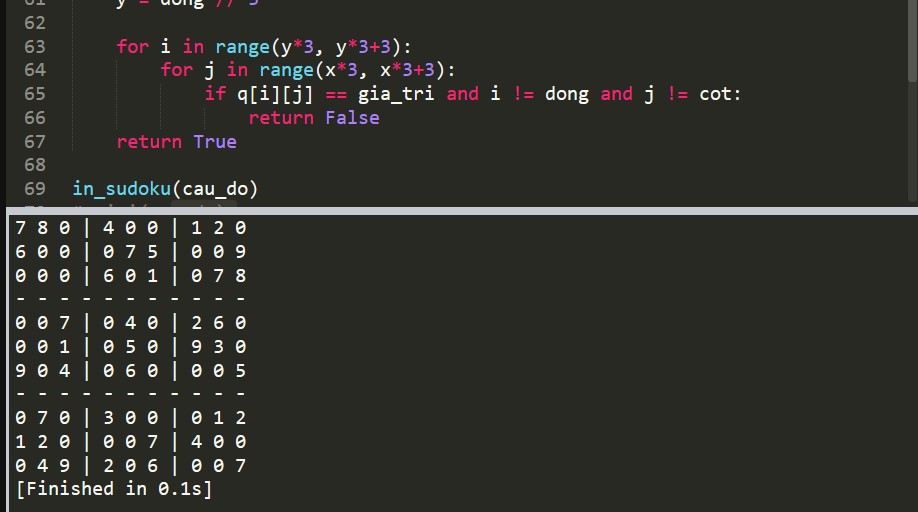
Mời các bạn xem chi tiết trong bài Thuật toán giải sudoku bằng quay lui backtracking

3.3. Sử dụng quay lui để giải bài toán xếp hậu

Xét bàn cờ tổng quát kích thước nxn. Một quân hậu trên bàn cờ có thể ăn được các quân khác nằm tại các ô cùng hàng, cùng cột hoặc cùng đường chéo. Hãy tìm các xếp n quân hậu trên bàn cờ sao cho không quân nào ăn quân nào. Mời bạn xem chi tiết trong bài Python: Bài toán xếp hậu sử dụng đệ quy

bài toán xếp hậu với n=8

4. Đặc điểm của thuật toán quay lui

Từ khóa » Thuật Toán đệ Quy Quay Lui Trong Java