Thuật Toán QuickSort - Giới Thiệu Chi Tiết Và Code Ví Dụ Trên Nhiều ...
Có thể bạn quan tâm
🔥CHỌN LỌC TOP NHỮNG KHOÁ HỌC LẬP TRÌNH ONLINE NHIỀU NGƯỜI THEO HOC TẠI ĐÂY🔥
Chào ace, bài này chúng ta sẽ tìm hiểu về một trong các thuật toán sắp xếp được sử dụng nhiều trong lập trình và thực tế nhất đó là QuickSort, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, ứng dụng của nó, code ví dụ, điểm mạnh, điểm yếu…) về QuickSort thông qua các phần sau.
1. Giới thiệu
Giống như Merge Sort, QuickSort là một thuật toán Chia và Chinh phục. Nó chọn một phần tử làm trục và phân vùng mảng đã cho xung quanh trục đã chọn. Có nhiều phiên bản khác nhau của QuickSort chọn pivot theo những cách khác nhau.
- Luôn chọn phần tử đầu tiên làm trục.
- Luôn chọn phần tử cuối cùng làm trụ (được triển khai bên dưới)
- Chọn một phần tử ngẫu nhiên làm trục quay.
- Chọn trung vị làm trục.
Quá trình quan trọng trong quickSort là partition(). Mục tiêu của phân vùng là, cho một mảng và một phần tử x của mảng làm trụ, đặt x vào đúng vị trí của nó trong mảng đã sắp xếp và đặt tất cả các phần tử nhỏ hơn (nhỏ hơn x) trước x và đặt tất cả các phần tử lớn hơn (lớn hơn x) sau x. Tất cả điều này nên được thực hiện trong thời gian tuyến tính.
Mã giả hàm QuickSort đệ quy:
/ * thấp -> Chỉ số bắt đầu, cao -> Chỉ số kết thúc * / quickSort(arr[], low, high) { if (low < high) { / * pi là chỉ mục phân vùng, arr[pi] bây giờ là ở đúng nơi * / pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Before pi quickSort(arr, pi + 1, high); // After pi } }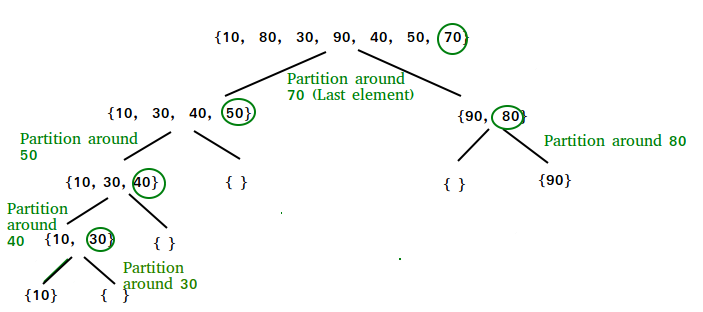
Thuật toán phân vùng
Có thể có nhiều cách để thực hiện phân vùng, sau mã giả áp dụng phương pháp được đưa ra trong sách CLRS. Logic rất đơn giản, chúng tôi bắt đầu từ phần tử ngoài cùng bên trái và theo dõi chỉ số của các phần tử nhỏ hơn (hoặc bằng) là i. Trong khi duyệt, nếu chúng tôi tìm thấy một phần tử nhỏ hơn, chúng tôi hoán đổi phần tử hiện tại với arr [i]. Nếu không, chúng ta bỏ qua phần tử hiện tại.
/ * thấp -> Chỉ số bắt đầu, cao -> Chỉ số kết thúc * / quickSort(arr[], low, high) { if (low < high) { / * pi là chỉ mục phân vùng, arr [pi] bây giờ là ở đúng nơi * / pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Before pi quickSort(arr, pi + 1, high); // After pi } }Mã giả cho partition()
/ * Hàm này nhận phần tử cuối cùng làm trục, vị trí phần tử xoay ở vị trí chính xác của nó trong mảng được sắp xếp và đặt tất cả nhỏ hơn (nhỏ hơn pivot) ở bên trái của trục và tất cả các phần tử lớn hơn ở bên phải trong tổng số trục * / partition (arr[], low, high) { // pivot (Element to be placed at right position) pivot = arr[high]; i = (low - 1) // Index of smaller element for (j = low; j <= high- 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap arr[i] and arr[j] } } swap arr[i + 1] and arr[high]) return (i + 1) }Hình minh họa partition():
arr [] = {10, 80, 30, 90, 40, 50, 70} Chỉ số: 0 1 2 3 4 5 6 low = 0, high = 6, pivot = arr [h] = 70 Khởi tạo chỉ mục của phần tử nhỏ hơn, i = -1 Di chuyển các phần tử từ j = low đến high-1 j = 0: Vì arr [j] <= pivot, do i ++ và hoán đổi (arr [i], arr [j]) i = 0 arr [] = {10, 80, 30, 90, 40, 50, 70} // Không thay đổi vì i và j // là tương tự nhau j = 1: Vì arr [j]> pivot, không làm gì cả // Không thay đổi trong i và arr [] j = 2: Vì arr [j] <= pivot, do i ++ và hoán đổi (arr [i], arr [j]) i = 1 arr [] = {10, 30, 80, 90, 40, 50, 70} // Chúng ta hoán đổi 80 và 30 j = 3: Vì arr [j]> pivot, không làm gì cả // Không thay đổi trong i và arr [] j = 4: Vì arr [j] <= pivot, do i ++ và hoán đổi (arr [i], arr [j]) i = 2 arr [] = {10, 30, 40, 90, 80, 50, 70} // 80 và 40 được hoán đổi j = 5: Vì arr [j] <= pivot, do i ++ và hoán đổi arr [i] với arr [j] i = 3 arr [] = {10, 30, 40, 50, 80, 90, 70} // 90 và 50 được hoán đổi Chúng ta đi ra khỏi vòng lặp vì j bây giờ bằng high-1. Cuối cùng, chúng ta đặt trục ở vị trí chính xác bằng cách hoán đổi arr [i + 1] và arr [high] (hoặc pivot) arr [] = {10, 30, 40, 50, 70, 90, 80} // 80 và 70 được hoán đổi Bây giờ 70 đã ở đúng vị trí của nó. Tất cả các phần tử nhỏ hơn 70 ở trước nó và tất cả các phần tử lớn hơn 70 là sau nó.2. Code ví dụ trên nhiều ngôn ngữ
C++
/* C++ implementation of QuickSort */ #include <bits/stdc++.h> using namespace std; // A utility function to swap two elements void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition (int arr[], int low, int high) { int pivot = arr[high]; // pivot int i = (low - 1); // Index of smaller element for (int j = low; j <= high - 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } /* The main function that implements QuickSort arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void quickSort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[p] is now at right place */ int pi = partition(arr, low, high); // Separately sort elements before // partition and after partition quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Driver Code int main() { int arr[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(arr) / sizeof(arr[0]); quickSort(arr, 0, n - 1); cout << "Sorted array: \n"; printArray(arr, n); return 0; }C
/* C implementation QuickSort */ #include<stdio.h> // A utility function to swap two elements void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition (int arr[], int low, int high) { int pivot = arr[high]; // pivot int i = (low - 1); // Index of smaller element for (int j = low; j <= high- 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } /* The main function that implements QuickSort arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void quickSort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[p] is now at right place */ int pi = partition(arr, low, high); // Separately sort elements before // partition and after partition quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i=0; i < size; i++) printf("%d ", arr[i]); printf("\n"); } // Driver program to test above functions int main() { int arr[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(arr)/sizeof(arr[0]); quickSort(arr, 0, n-1); printf("Sorted array: \n"); printArray(arr, n); return 0; }Java
// Java program for implementation of QuickSort class QuickSort { /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition(int arr[], int low, int high) { int pivot = arr[high]; int i = (low-1); // index of smaller element for (int j=low; j<high; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // swap arr[i] and arr[j] int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } // swap arr[i+1] and arr[high] (or pivot) int temp = arr[i+1]; arr[i+1] = arr[high]; arr[high] = temp; return i+1; } /* The main function that implements QuickSort() arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void sort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[pi] is now at right place */ int pi = partition(arr, low, high); // Recursively sort elements before // partition and after partition sort(arr, low, pi-1); sort(arr, pi+1, high); } } /* A utility function to print array of size n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // Driver program public static void main(String args[]) { int arr[] = {10, 7, 8, 9, 1, 5}; int n = arr.length; QuickSort ob = new QuickSort(); ob.sort(arr, 0, n-1); System.out.println("sorted array"); printArray(arr); } }Python
# Python program for implementation of Quicksort Sort # This function takes last element as pivot, places # the pivot element at its correct position in sorted # array, and places all smaller (smaller than pivot) # to left of pivot and all greater elements to right # of pivot def partition(arr,low,high): i = ( low-1 ) # index of smaller element pivot = arr[high] # pivot for j in range(low , high): # If current element is smaller than the pivot if arr[j] < pivot: # increment index of smaller element i = i+1 arr[i],arr[j] = arr[j],arr[i] arr[i+1],arr[high] = arr[high],arr[i+1] return ( i+1 ) # The main function that implements QuickSort # arr[] --> Array to be sorted, # low --> Starting index, # high --> Ending index # Function to do Quick sort def quickSort(arr,low,high): if low < high: # pi is partitioning index, arr[p] is now # at right place pi = partition(arr,low,high) # Separately sort elements before # partition and after partition quickSort(arr, low, pi-1) quickSort(arr, pi+1, high) # Driver code to test above arr = [10, 7, 8, 9, 1, 5] n = len(arr) quickSort(arr,0,n-1) print ("Sorted array is:") for i in range(n): print ("%d" %arr[i]),C#
// C# program for implementation of QuickSort using System; class GFG { /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ static int partition(int []arr, int low, int high) { int pivot = arr[high]; // index of smaller element int i = (low - 1); for (int j = low; j < high; j++) { // If current element is smaller // than the pivot if (arr[j] < pivot) { i++; // swap arr[i] and arr[j] int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } // swap arr[i+1] and arr[high] (or pivot) int temp1 = arr[i+1]; arr[i+1] = arr[high]; arr[high] = temp1; return i+1; } /* The main function that implements QuickSort() arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ static void quickSort(int []arr, int low, int high) { if (low < high) { /* pi is partitioning index, arr[pi] is now at right place */ int pi = partition(arr, low, high); // Recursively sort elements before // partition and after partition quickSort(arr, low, pi-1); quickSort(arr, pi+1, high); } } // A utility function to print array of size n static void printArray(int []arr, int n) { for (int i = 0; i < n; ++i) Console.Write(arr[i] + " "); Console.WriteLine(); } // Driver program public static void Main() { int []arr = {10, 7, 8, 9, 1, 5}; int n = arr.Length; quickSort(arr, 0, n-1); Console.WriteLine("sorted array "); printArray(arr, n); } }Kết quả
Sorted array: 1 5 7 8 9 103. Độ phức tạp
Thời gian thực hiện bởi QuickSort nói chung có thể được viết như sau.
T(n) = T(k) + T(n-k-1) + θ(n)Hai thuật ngữ đầu tiên dành cho hai cuộc gọi đệ quy, thuật ngữ cuối cùng dành cho tiến trình phân vùng. k là số phần tử nhỏ hơn pivot.
Thời gian thực hiện bởi QuickSort phụ thuộc vào mảng đầu vào và chiến lược phân vùng. Sau đây là ba trường hợp.
Trường hợp xấu nhất: Trường hợp xấu nhất xảy ra khi quá trình phân vùng luôn chọn phần tử lớn nhất hoặc nhỏ nhất làm pivot. Nếu chúng ta xem xét chiến lược phân vùng ở trên, nơi phần tử cuối cùng luôn được chọn làm trục, trường hợp xấu nhất sẽ xảy ra khi mảng đã được sắp xếp theo thứ tự tăng hoặc giảm. Sau đây là tái diễn cho trường hợp xấu nhất.
T(n) = T(0) + T(n-1) + θ(n) tương đương với T(n) = T(n-1) + θ(n)Giải pháp của sự lặp lại ở trên là: θ(n2).
Trường hợp tốt nhất: Trường hợp tốt nhất xảy ra khi quá trình phân vùng luôn chọn phần tử ở giữa làm trục. Sau đây là tái diễn cho trường hợp tốt nhất.
T(n) = 2T(n/2) + θ(n)Giải pháp của sự lặp lại ở trên là θ (nLogn). Nó có thể được giải quyết bằng cách sử dụng trường hợp 2 của Định lý Master.
Trường hợp trung bình:
Để thực hiện phân tích trường hợp trung bình, chúng ta cần xem xét tất cả các hoán vị có thể có của mảng và tính toán thời gian thực hiện cho mọi hoán vị, điều này có vẻ không dễ dàng.
Chúng ta có thể có ý tưởng về trường hợp trung bình bằng cách xem xét trường hợp khi phân hoạch đặt O (n / 9) phần tử trong một tập hợp và O (9n / 10) phần tử trong tập hợp khác. Sau đây là tái diễn cho trường hợp này.
T(n) = T(n/9) + T(9n/10) + θ(n)Giải pháp của sự tái diễn trên cũng là O (nLogn)
Mặc dù độ phức tạp thời gian trong trường hợp xấu nhất của QuickSort là O (n2), cao hơn nhiều thuật toán sắp xếp khác như Merge Sort và Heap Sort, QuickSort trên thực tế nhanh hơn, vì vòng lặp bên trong của nó có thể được triển khai hiệu quả trên hầu hết các kiến trúc và hầu hết các -dữ liệu thế giới. QuickSort có thể được thực hiện theo nhiều cách khác nhau bằng cách thay đổi sự lựa chọn của trục, do đó trường hợp xấu nhất hiếm khi xảy ra đối với một loại dữ liệu nhất định. Tuy nhiên, sắp xếp hợp nhất thường được coi là tốt hơn khi dữ liệu lớn và được lưu trữ trong bộ nhớ ngoài.
QuickSort có ổn định không?
Việc triển khai mặc định không ổn định. Tuy nhiên, bất kỳ thuật toán sắp xếp nào cũng có thể ổn định bằng cách coi các chỉ mục là tham số so sánh.
QuickSort có tại chỗ không?
Theo định nghĩa rộng của thuật toán tại chỗ, nó đủ điều kiện là thuật toán sắp xếp tại chỗ vì nó chỉ sử dụng thêm không gian để lưu trữ các lệnh gọi hàm đệ quy chứ không phải để thao tác đầu vào.
QuickSort 3 cách là gì?
Trong thuật toán QuickSort đơn giản, chúng tôi chọn một phần tử làm pivot, phân vùng mảng xung quanh pivot và lặp lại cho các mảng con ở bên trái và bên phải của pivot.
Hãy xem xét một mảng có nhiều phần tử dư thừa. Ví dụ: {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}. Nếu 4 được chọn làm trụ trong QuickSort đơn giản, chúng ta chỉ sửa một 4 và xử lý đệ quy các lần xuất hiện còn lại. Trong QuickSort 3 cách, một mảng arr [l..r] được chia thành 3 phần:
a) arr [l..i] phần tử nhỏ hơn pivot.
b) arr [i + 1..j-1] phần tử bằng pivot.
c) arr [j..r] phần tử lớn hơn pivot.
Xem điều này để thực hiện.
Làm thế nào để triển khai QuickSort cho Danh sách được Liên kết?
QuickSort trên danh sách liên kết Singly
QuickSort trên danh sách được liên kết kép
Chúng ta có thể triển khai QuickSort lặp lại theo cách thức không?
Có, vui lòng tham khảo Sắp xếp nhanh lặp lại.
Tại sao Sắp xếp Nhanh được ưu tiên hơn Merge Sort để sắp xếp Mảng
Sắp xếp nhanh ở dạng chung là sắp xếp tại chỗ (tức là không yêu cầu thêm dung lượng) trong khi sắp xếp hợp nhất yêu cầu thêm O (N) bộ nhớ, N biểu thị kích thước mảng có thể khá đắt. Việc phân bổ và loại bỏ không gian thừa được sử dụng để sắp xếp hợp nhất làm tăng thời gian chạy của thuật toán. So sánh độ phức tạp trung bình, chúng tôi thấy rằng cả hai kiểu sắp xếp đều có độ phức tạp trung bình O (NlogN) nhưng các hằng số khác nhau. Đối với mảng, sắp xếp hợp nhất bị mất do sử dụng thêm không gian lưu trữ O (N).
Hầu hết các triển khai thực tế của Sắp xếp nhanh đều sử dụng phiên bản ngẫu nhiên. Phiên bản ngẫu nhiên có độ phức tạp thời gian dự kiến là O (nLogn). Trường hợp xấu nhất cũng có thể xảy ra trong phiên bản ngẫu nhiên, nhưng trường hợp xấu nhất không xảy ra đối với một mẫu cụ thể (như mảng được sắp xếp) và Sắp xếp nhanh ngẫu nhiên hoạt động tốt trong thực tế.
Quick Sort cũng là một thuật toán sắp xếp thân thiện với bộ nhớ cache vì nó có vị trí tham chiếu tốt khi được sử dụng cho các mảng.
Sắp xếp nhanh cũng là đệ quy đuôi, do đó tối ưu hóa cuộc gọi đuôi được thực hiện.
Tại sao MergeSort được ưa thích hơn QuickSort cho các Danh sách được Liên kết?
Trong trường hợp danh sách liên kết, trường hợp này khác nhau chủ yếu do sự khác biệt trong phân bổ bộ nhớ của mảng và danh sách liên kết. Không giống như mảng, các nút danh sách liên kết có thể không liền kề trong bộ nhớ. Không giống như mảng, trong danh sách liên kết, chúng ta có thể chèn các mục vào giữa trong O (1) không gian thừa và O (1) thời gian. Do đó hoạt động hợp nhất của sắp xếp hợp nhất có thể được thực hiện mà không có thêm dung lượng cho danh sách được liên kết.
Trong mảng, chúng ta có thể thực hiện truy cập ngẫu nhiên vì các phần tử liên tục trong bộ nhớ. Giả sử chúng ta có một mảng A số nguyên (4 byte) và đặt địa chỉ của A [0] là x thì để truy cập A [i], chúng ta có thể truy cập trực tiếp vào bộ nhớ tại (x + i * 4). Không giống như mảng, chúng ta không thể thực hiện truy cập ngẫu nhiên trong danh sách liên kết. Sắp xếp nhanh yêu cầu rất nhiều loại truy cập. Trong danh sách liên kết để truy cập chỉ mục thứ i, chúng ta phải di chuyển từng nút từ đầu đến nút thứ i vì chúng ta không có khối bộ nhớ liên tục. Do đó, chi phí tăng lên để sắp xếp nhanh chóng. Sắp xếp hợp nhất truy cập dữ liệu một cách tuần tự và nhu cầu truy cập ngẫu nhiên thấp.
Nguồn và Tài liệu tiếng anh tham khảo:
- w3schools
- Geeksforgeeks
- codechef
- dev.to
Tài liệu từ cafedev:
- Full series tự học Cấu trúc dữ liệu và giải thuật từ cơ bản tới nâng cao tại đây nha.
- Ebook về Cấu trúc dữ liệu và giải thuật tại đây.
- Các series tự học lập trình khác
Nếu bạn thấy hay và hữu ích, bạn có thể tham gia các kênh sau của cafedev để nhận được nhiều hơn nữa:
- Group Facebook
- Fanpage
- Youtube
- Trang chủ
Chào thân ái và quyết thắng!
Đăng ký kênh youtube để ủng hộ Cafedev nha các bạn, Thanks you!
Từ khóa » độ Phức Tạp Của Thuật Toán Quick Sort
-
Thuật Toán Quick Sort Là Gì? Giới Thiệu Lập Trình Chi Tiết Nhất - Teky
-
Tìm Hiểu Thuật Toán Quick Sort - Viblo
-
Độ Phức Tạp Của Thuật Toán Quicksort - Chienlubo
-
Quick Sort Là Gì? Tìm Hiểu Chi Tiết Về Quick Sort - Tino Group
-
Sắp Xếp Quicksort - VietCodes
-
Thuật Toán Quick Sort Là Gì? - TopDev
-
Độ Phức Tạp Của Thuật Toán Quicksort, Sắp Xếp Nhanh
-
So Sánh độ Phức Tạp Của Thuật Toán Quicksort & Insertsort - Tài Liệu Text
-
Độ Phức Tạp Của Thuật Toán Quick Sort - Kiemvuongchimong
-
Độ Phức Tạp Của Thuật Toán Và Lựa Chọn Cách Giải Thuật
-
Độ Phức Tạp Của Thuật Toán Quicksort? - Tạo Website
-
Sắp Xếp Nhanh – Wikipedia Tiếng Việt
-
[PDF] BÀI 7: SẮP XẾP - Topica
-
Thuật Toán Sắp Xếp Nhanh - Quick Sort Algorithm C/C++