Tìm Các GTLN Của Hàm Số Y = 2sinx - 4/3sin^3x Trên [0;π] - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
 Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- Pham Trong Bach
GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là
A. 1
B. 3 2
C. 2
D. 7 4
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  1 tháng 4 2018 lúc 8:40
1 tháng 4 2018 lúc 8:40 Xét hàm số y=2sin x + cos 2x trên đoạn
y’=2cos x- 2sin 2x = 2cos x(1- 2sin x)
Trên đoạn [0; π]
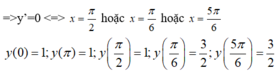
Giá trị lớn nhất của hàm số này trên [0; π] là y = 3 2 .
Chọn B
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Thảo Châu
Tìm các GTLN của hàm số y = 2sinx - 4/3sin^3x trên [0;π]
Xem chi tiết Lớp 12 Toán Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của h... 0 0 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  16 tháng 3 2018 lúc 2:17
16 tháng 3 2018 lúc 2:17 a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  10 tháng 4 2019 lúc 17:20
10 tháng 4 2019 lúc 17:20 f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 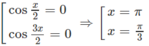
Ta có: f(0) = 0,
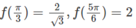
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Thùy Linh Hà
Tìm GTLN, GTNN của hàm số y = sinx + cosx trên đoạn [ π/4 ; π/2 ]
Xem chi tiết Lớp 11 Toán Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GI... 0 0 Gửi Hủy
Gửi Hủy 
- An Hoài Nguyễn
1. Hàm số y =2sinx+cos2x , x€ [0;π) đồng biến trên khoảng nào? 2. Hàm số y=|x^2-2x-3| nghịch buến trên khoảng nào?
Xem chi tiết Lớp 12 Toán Bài 1: Sự đồng biến và nghịch biến của hàm số 2 0 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm
Nguyễn Việt Lâm  18 tháng 6 2021 lúc 18:19
18 tháng 6 2021 lúc 18:19 1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
Đúng 1 Bình luận (2) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm
Nguyễn Việt Lâm  18 tháng 6 2021 lúc 18:21
18 tháng 6 2021 lúc 18:21 2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
Đúng 0 Bình luận (2) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm GTLN và GTNN của hàm số: y = 2 sin x + cos x + 3 2 cos x - sin x + 4
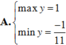
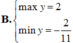
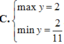
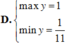
 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  18 tháng 10 2018 lúc 10:31
18 tháng 10 2018 lúc 10:31 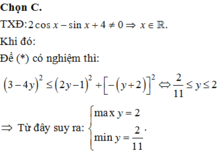
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là
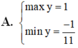
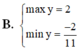
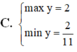
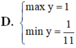
 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  21 tháng 9 2017 lúc 7:31
21 tháng 9 2017 lúc 7:31 Đáp án C
TXĐ:![]()
- Khi đó:
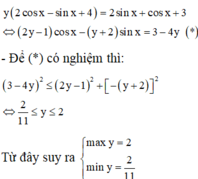
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là:
A. m a x y = 1 m i n y = - 1 11
B. m a x y = 2 m i n y = - 2 11
C. m a x y = 2 m i n y = 2 11
D. m a x y = 1 m i n y = 1 11
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  4 tháng 6 2019 lúc 8:31
4 tháng 6 2019 lúc 8:31 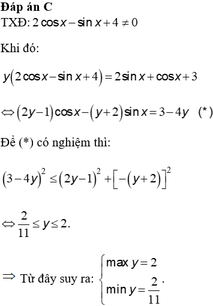
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
GTLN của hàm số y = sin 2 x - 3 cos x trên đoạn [0; π] là
A. 1
B. 7 4
C. 2
D. 1 4
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  2 tháng 3 2018 lúc 7:37
2 tháng 3 2018 lúc 7:37 Chọn B
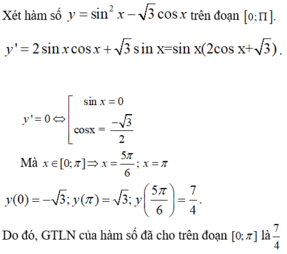
 Gửi Hủy
Gửi Hủy Từ khóa » Gtln Và Gtnn Của Hàm Số Y = 2sinx – Sin3x Trên đoạn 0 Là
-
Câu 37. GTLN Và GTNN Của Hàm Số: Y = 2sinx – \(\frac{4}{3}\)sin3x ...
-
[LỜI GIẢI] Tìm Giá Trị Lớn Nhất Nhỏ Nhất Của Hàm Số: Y = 2sinx
-
Giá Trị Lớn Nhất Của Hàm Số Y = 2sinx - 4/3sin^3x Trên [0; π]
-
Tìm Min, Max Của Hàm Số Y=sin^3x-3sinx+1 Trên [0,π] Câu Hỏi 23348
-
GTLN Của Hàm Số Y = 2sinx + Cos2x Trên đoạn [0; Pi] Là 1 - Khóa Học
-
Tìm GTLN, GTNN Của Hàm Số Y= -9sinx - Sin3x - Tran Sa - Hoc247
-
Giá Trị Nhỏ Nhất Của Hàm Số Y = 2sinx - 3
-
Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Y = Sin X Trên đo
-
Bài Tập Giá Trị Lớn Nhất – Giá Trị Nhỏ Nhất
-
Cho Hàm Số Y = Sin3x - 3sinx + 1 Xét Trên (0;π). GTLN Của ...
-
Tìm Tập Giá Trị Lớn Nhất, Giá Trị Nhỏ Nhất Của Hàm Số Y= 4 - 3sin^2(2x)...
-
[PDF] TÀI LIỆU HỌC TẬP MIỄN PHÍ Group: Https://www ... - HOC360.NET
-
Tìm Giá Trị Lớn Nhất M Và Giá Trị Nhỏ Nhất M Của Hàm Số Y=3sinx
-
Tiết 1. Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số - TaiLieu.VN