Tìm Các Khoảng đồng Biến, Nghịch Biến Của Hàm Số Dựa Vào đồ Thị ...

Có thể bạn quan tâm

Tìm các khoảng đồng biến, nghịch biến của hàm số dựa vào đồ thị và bảng biến thiên

Phương pháp giải đồng biến nghịch biến – đơn điệu hàm số

Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải, nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

Chú ý tập xác định của hàm số.

Bài tập xét tính đồng biên nghịch biến

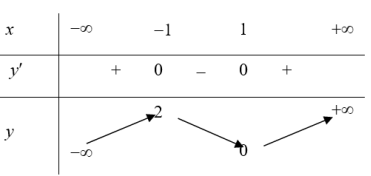
Ví dụ 1: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ

Khẳng định nào sau đây là đúng.

A. Hàm số đồng biến trên khoảng $\left( -\infty ;2 \right)$.

B. Hàm số nghịch biến trên khoảng $\left( -1;0 \right)$.

C. Hàm số nghịch biến trên khoảng $\left( 0;2 \right)$.

D. Hàm số đồng biến trên $\mathbb{R}$.

Lời giải chi tiết

Dựa vào bảng biến thiên ta thấy: Hàm số nghịch biến trên khoảng $\left( -1;1 \right)$ và đồng biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$ Þ Hàm số nghịch biến trên khoảng $\left( -1;0 \right)$. Chọn B.

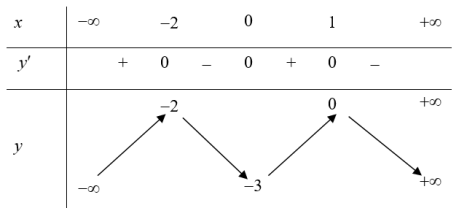
Ví dụ 2: Cho hàm số có bảng biến thiên như hình vẽ

Khẳng định nào sau đây là đúng.

A. Hàm số đồng biến trên khoảng $\left( -\infty ;-2 \right)$và$\left( -3;0 \right)$. B. Hàm số nghịch biến trên khoảng $\left( -3;-2 \right)$.

C. Hàm số đồng biến trên khoảng $\left( 0;1 \right)$. D. Hàm số nghịch biến trên khoảng $\left( 0;+\infty \right)$.

Lời giải chi tiết

Dựa vào bảng biến thiên ta thấy: Hàm số đồng biến trên các khoảng $\left( -\infty ;2 \right)$và $\left( 0;1 \right)$.

Hàm số nghịch biến trên các khoảng $\left( -2;0 \right)$ và $\left( 1;+\infty \right)$. Chọn B.

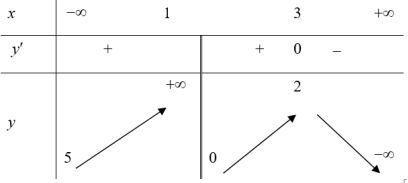
Ví dụ 3: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ.

Khẳng định nào sau đây là đúng.

A. Hàm số đồng biến trên khoảng $\left( -\infty ;3 \right)$. B. Hàm số nghịch biến trên khoảng $\left( 2;+\infty \right)$.

C. Hàm số đồng biến trên $\left( -\infty ;1 \right)\cup \left( 1;3 \right)$. D. Hàm số đồng biến trên $\left( -\infty ;1 \right)$ và $\left( 1;3 \right)$.

Lời giải chi tiết

Hàm số xác định trên tập $\mathbb{R}\backslash \left\{ 1 \right\}$.

Dựa vào bảng biến thiên suy ra hàm số đồng biến trên các khoảng $\left( -\infty ;1 \right)$ và $\left( 1;3 \right)$. Hàm số nghịch biến trên khoảng $\left( 3;+\infty \right)$. Chọn D.

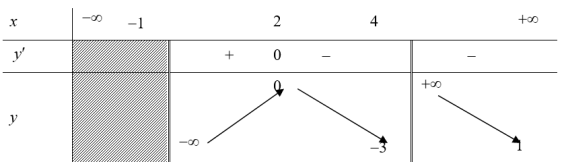
Ví dụ 4: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ

Khẳng định nào sau đây đúng.

A. Hàm số đồng biến trên khoảng $\left( -\infty ;2 \right)$.

B. Hàm số nghịch biến trên khoảng $\left( 2;+\infty \right)$.

C. Hàm số nghịch biến trên mỗi khoảng $\left( 2;4 \right)$ và $\left( 4;+\infty \right)$.

D. Hàm số đồng biến trên khoảng $\left( -\infty ;0 \right)$.

Lời giải chi tiết

Tập xác định của hàm số là: $\left( -1;+\infty \right)\backslash \left\{ 4 \right\}$.

Dựa vào bảng biến thiên suy ra hàm số đồng biến trên khoảng $\left( -1;2 \right)$ và nghịch biến trên mỗi khoảng $\left( 2;4 \right)$ và $\left( 4;+\infty \right)$. Chọn C.

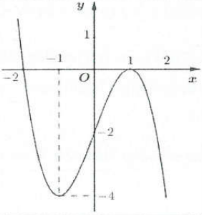
Ví dụ 5: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên.

Hàm số đã cho đồng biến trên khoảng.

A. $\left( -1;1 \right)$

B. $\left( -\infty ;-2 \right)$

C. $\left( 1;+\infty \right)$

D. $\left( -2;1 \right)$

Lời giải chi tiết

Dựa vào đồ thị hàm số suy ra hàm số đồng biến trên khoảng $\left( -1;1 \right)$ và nghịch biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$. Chọn A.

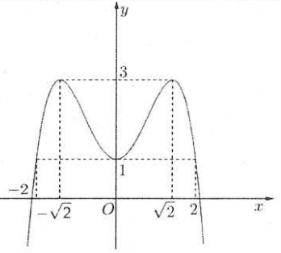
Ví dụ 6: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên.

Hàm số đã cho đồng biến trên khoảng.

A. $\left( -\sqrt{2};\sqrt{2} \right)$.

B. $\left( -2;2 \right)$.

C. $\left( 1;3 \right)$.

D. $\left( 0;\sqrt{2} \right)$.

Lời giải chi tiết

Dựa vào đồ thị hàm số suy ra hàm số đồng biến trên khoảng $\left( -\infty ;-\sqrt{2} \right),\left( 0;\sqrt{2} \right)$ và nghịch biến trên các khoảng $\left( -\sqrt{2};0 \right)$ và $\left( \sqrt{2};+\infty \right)$. Chọn D.

Từ khóa » Hàm Số đồng Biến Trên Khoảng Nào

Tìm Các Khoảng đồng Biến, Nghịch Biến Của Hàm Số Dựa Vào đồ Thị ...