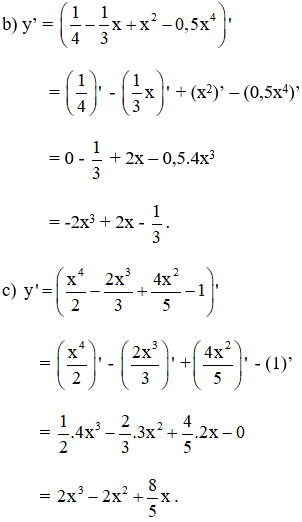Tìm đạo Hàm Của Các Hàm Số Sau: A) Y = X^5 - 4x^3 + 2x - 3 B) Y = 1/4

Có thể bạn quan tâm

Đăng nhập Facebook

Google

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

23/07/2024 23,870

Tìm đạo hàm của các hàm số sau:

a) y=x5-4x3+2x-3;

b) y=14-13x+x2-0,5x4;

c) y= x42-2x33+4x25-1;

d) y=3x5(8-3x2).

Xem lời giải Câu hỏi trong đề: Giải SGK Toán 11 Chương 5: Đạo hàm Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

a) y’ = (x5– 4x3+ 2x – 3)’

= (x5)’ – (4x3)’ + (2x)’ – (3)’

= 5x4– 4.3x2+ 2

= 5x4– 12x2+ 2.

d) Cách 1 : y = 3x5(8 - 3x2)

= 3x5.8 – 3x5.3x2= 24x5– 9x7

⇒ y’ = (24x5– 9x7)’

= (24x5)' – (9x7)’

= 24.5x4– 9.7x6

= 120x4– 63x6.

Cách 2 : Áp dụng công thức tính đạo hàm của tích :

⇒ y’ = [(3x5)’].(8 – 3x2) + 3x5.[(8 – 3x2)’]

= 3.5x4(8 – 3x2) + 3x5.[(8)’ – (3x2)’]

= 15x4(8 – 3x2) + 3x5.(0 – 3.2x)

= 15x4.8 – 15x4.3x2+ 3x5.(-6x)

= 120x4– 45x6– 18x6

= 120x4– 63x6.

Câu trả lời này có hữu ích không?

1 0

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm đạo hàm của các hàm số sau:

a. y= x7-5x23

b. y=x2+15-3x2

c. y=2xx2-1

d. y=3-5xx2-x+1

e. y=m+nx23 (m, n là các hằng số)

Xem đáp án » 30/11/2021 11,664

Câu 2:

Cho y=x3-3x2+2. Tìm x để:

a. y' > 0

b. y' < 3

Xem đáp án » 30/11/2021 3,087

Câu 3:

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a. y = 7 + x – x2 tại x0= 1

b. y = x3– 2x + 1 tại x0= 2.

Xem đáp án » 30/11/2021 2,368

Câu 4:

Chứng minh khẳng định trong nhận xét trên.

a) Đạo hàm của hàm hằng bằng 0: c’ = 0.

b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Xem đáp án » 30/11/2021 2,146

Câu 5:

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số

y = 5x3 - 2x5; y=-x3.x.

Xem đáp án » 30/11/2021 1,592

Câu 6:

Tính đạo hàm của các hàm số sau:

a) y=x2-xx+1;

b) y=2-5x-x2;

c) y=x3a2-x2 (a là hằng số);

d) y=1+x1-x.

Xem đáp án » 30/11/2021 865

Câu 7:

Dùng định nghĩa tính đạo hàm của hàm số y = x3 tại điểm x tùy ý.

Dự đoán đạo hàm của hàm số y = x100 tại điểm x.

Xem đáp án » 30/11/2021 581

Câu 8:

Hàm số y=x2+x+1 là hàm hợp của hàm số nào ?

Xem đáp án » 30/11/2021 362

Câu 9:

Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 160: Hãy chứng minh các công thức trên và lấy ví dụ minh họa.

Xem đáp án » 30/11/2021 215 Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 22949 lượt thi Thi thử
Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8267 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 4836 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4059 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 3782 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3715 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3198 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3132 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3064 lượt thi Thi thử
Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3042 lượt thi Thi thử

Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?
250 18/04/2024 Xem đáp án
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?
138 18/04/2024 Xem đáp án
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Tính chu kì của hàm số h(t)?
121 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = sin x, tìm:
Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 128 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = sin x, tìm:

Các giá trị của x để sin x = \(\frac{1}{2}\);
121 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = cos x, cho biết:

Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.
115 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = cos x, cho biết:

Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;
118 18/04/2024 Xem đáp án
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).
121 18/04/2024 Xem đáp án
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);
121 18/04/2024 Xem đáp án
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

\(y = \frac{1}{{4 - \sin x}}\).
127 18/04/2024 Xem đáp án

Xem thêm »

Từ khóa » đạo Hàm Của X/4-1

Tìm đạo Hàm Của Các Hàm Số Sau: A) Y = X^5 - 4x^3 + 2x - 3 B) Y = 1/4

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm đạo hàm của các hàm số sau:

a. y= x7-5x23

b. y=x2+15-3x2

c. y=2xx2-1

d. y=3-5xx2-x+1

e. y=m+nx23 (m, n là các hằng số)

Câu 2:

Cho y=x3-3x2+2. Tìm x để:

a. y' > 0

b. y' < 3

Câu 3:

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a. y = 7 + x – x2 tại x0= 1

b. y = x3– 2x + 1 tại x0= 2.

Câu 4:

Chứng minh khẳng định trong nhận xét trên.

a) Đạo hàm của hàm hằng bằng 0: c’ = 0.

b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Câu 5:

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số

y = 5x3 - 2x5; y=-x3.x.

Câu 6:

Tính đạo hàm của các hàm số sau:

a) y=x2-xx+1;

b) y=2-5x-x2;

c) y=x3a2-x2 (a là hằng số);

d) y=1+x1-x.

Câu 7:

Dùng định nghĩa tính đạo hàm của hàm số y = x3 tại điểm x tùy ý.

Dự đoán đạo hàm của hàm số y = x100 tại điểm x.

Câu 8:

Hàm số y=x2+x+1 là hàm hợp của hàm số nào ?

Câu 9:

Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 160: Hãy chứng minh các công thức trên và lấy ví dụ minh họa.

Đề thi liên quan

Câu hỏi mới nhất

Tìm Đạo Hàm - D/dx F(x)=1/(x^4) | Mathway

Tính đạo Hàm Của Hàm Số Y = (x^4+1)^ Căn 2 Y' = Căn 2(x ... - Khóa Học

Y = ( 1 ) / ( X4 ) | Xem Lời Giải Tại QANDA

Tính đạo Hàm Của Hàm Số Y = (x^4+1)^ Căn 2 Y' = Căn 2(x^4+1)^(1/1 ...

Tính đạo Hàm Của Hàm Số Y= X+1/4^x... - Vietjack.online

Tính đạo Hàm Của Hàm Số Y = ((x + 1))(((4^x))).

Cho \(f(x) = \ln ({x^4} + 1)\). Đạo Hàm F'(1) Bằng - HOC247

Tìm Hàm Số F(x) Biết F(x)=∫x^3/(x^4+1)dx Và F(0) = 1

Cho Hàm Số F( X ) Có đạo Hàm F'( X )=( X-1 )( X^2-3 )( X^4-1 ) Liên Tụ

Cho Hàm Số \(f(x) = \ln \left( {{x^4} + 1} \right).\) Tính đạo Hàm F'(1).

Cho Hàm Số F(x)=ln(x4+1) F ( X ) = Ln ⁡ ( X 4 + 1 ) . Đạo Hàm F'(0) Bằng

Tính đạo Hàm Của Hàm Số $f\left( X \right)=x\ln {{x}^{2}}$ Tại điểm X=4 ...

Liên Hệ

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm đạo hàm của các hàm số sau: a. y= x7-5x23 b. y=x2+15-3x2 c. y=2xx2-1 d. y=3-5xx2-x+1 e. y=m+nx23 (m, n là các hằng số)

Câu 2:

Cho y=x3-3x2+2. Tìm x để: a. y' > 0 b. y' < 3

Câu 3:

Bằng định nghĩa, tìm đạo hàm của các hàm số sau : a. y = 7 + x – x2 tại x0= 1 b. y = x3– 2x + 1 tại x0= 2.

Câu 4:

Chứng minh khẳng định trong nhận xét trên. a) Đạo hàm của hàm hằng bằng 0: c’ = 0. b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Câu 5:

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số y = 5x3 - 2x5; y=-x3.x.

Câu 6:

Tính đạo hàm của các hàm số sau: a) y=x2-xx+1; b) y=2-5x-x2; c) y=x3a2-x2 (a là hằng số); d) y=1+x1-x.

Câu 7:

Dùng định nghĩa tính đạo hàm của hàm số y = x3 tại điểm x tùy ý. Dự đoán đạo hàm của hàm số y = x100 tại điểm x.

Câu 8:

Hàm số y=x2+x+1 là hàm hợp của hàm số nào ?

Câu 9:

Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 160: Hãy chứng minh các công thức trên và lấy ví dụ minh họa.

Đề thi liên quan

Câu hỏi mới nhất

Liên Hệ

Tìm đạo hàm của các hàm số sau:

a. y= x7-5x23

b. y=x2+15-3x2

c. y=2xx2-1

d. y=3-5xx2-x+1

e. y=m+nx23 (m, n là các hằng số)

Cho y=x3-3x2+2. Tìm x để:

a. y' > 0

b. y' < 3

Bằng định nghĩa, tìm đạo hàm của các hàm số sau :

a. y = 7 + x – x2 tại x0= 1

b. y = x3– 2x + 1 tại x0= 2.

Chứng minh khẳng định trong nhận xét trên.

a) Đạo hàm của hàm hằng bằng 0: c’ = 0.

b) Đạo hàm của hàm số y = x bằng 1: x’ = 1.

Áp dụng các công thức trong Định lí 3, hãy tính đạo hàm của các hàm số

y = 5x3 - 2x5; y=-x3.x.

Tính đạo hàm của các hàm số sau:

a) y=x2-xx+1;

b) y=2-5x-x2;

c) y=x3a2-x2 (a là hằng số);

d) y=1+x1-x.

Dùng định nghĩa tính đạo hàm của hàm số y = x3 tại điểm x tùy ý.

Dự đoán đạo hàm của hàm số y = x100 tại điểm x.