Tìm đạo Hàm Của Các Hàm Số Sau: Y = Tan X Sin X - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
Pham Trong Bach 27 tháng 4 2019 lúc 17:58 Tìm đạo hàm của các hàm số sau: y = tan x sin x + 2
Lớp 11 Toán Những câu hỏi liên quan
- Bài 9.8 trang 94
-
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
Xem chi tiết Lớp 11 Toán Bài 32. Các quy tắc tính đạo hàm 1 0
Gửi Hủy 
Bùi Nguyên Khải 
17 tháng 8 2023 lúc 11:19 tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Đúng 1 Bình luận (0) Gửi Hủy - Bài 9 trang 51
-
Tinh đạo hàm của các hàm số sau:
a) \(y = \tan \left( {{e^x} + 1} \right)\);
b) \(y = \sqrt {\sin 3x} \);
c) \(y = \cot \left( {1 - {2^x}} \right)\).
Xem chi tiết Lớp 11 Toán Bài tập cuối chương VII 1 0
Gửi Hủy 
Nguyễn Lê Phước Thịnh CTV 
20 tháng 8 2023 lúc 20:31 a: \(y'=\left[tan\left(e^x+1\right)\right]'=\dfrac{\left(e^x+1\right)'}{cos^2\left(e^x+1\right)}=\dfrac{e^x}{cos^2\left(e^x+1\right)}\)
b: \(y'=\left(\sqrt{sin3x}\right)'\)
\(=\dfrac{\left(sin3x\right)'}{2\sqrt{sin3x}}=\dfrac{3\cdot cos3x}{2\sqrt{sin3x}}\)
c: \(y=cot\left(1-2^x\right)\)
=>\(y'=\left[cot\left(1-2^x\right)\right]'\)
\(=\dfrac{-2}{sin^2\left(1-2^x\right)}\cdot\left(-2^x\cdot ln2\right)\)
\(=\dfrac{2^{x+1}\cdot ln2}{sin^2\left(1-2^x\right)}\)
Đúng 1 Bình luận (0) Gửi Hủy - Bài 2 trang 49
-
Tính đạo hàm của các hàm số sau:
a) \(y = \sin 3x\);
b) \(y = {\cos ^3}2x\);
c) \(y = {\tan ^2}x\);
d) \(y = \cot \left( {4 - {x^2}} \right)\).
Xem chi tiết Lớp 11 Toán Bài 2. Các quy tắc tính đạo hàm 1 0 Gửi Hủy 
Hà Quang Minh Giáo viên CTVVIP 
22 tháng 9 2023 lúc 14:56 a) Đặt \(u = 3{\rm{x}}\) thì \(y = \sin u\). Ta có: \(u{'_x} = {\left( {3{\rm{x}}} \right)^\prime } = 3\) và \(y{'_u} = {\left( {\sin u} \right)^\prime } = \cos u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = \cos u.3 = 3\cos 3{\rm{x}}\).
Vậy \(y' = 3\cos 3{\rm{x}}\).
b) Đặt \(u = \cos 2{\rm{x}}\) thì \(y = {u^3}\). Ta có: \(u{'_x} = {\left( {\cos 2{\rm{x}}} \right)^\prime } = - 2\sin 2{\rm{x}}\) và \(y{'_u} = {\left( {{u^3}} \right)^\prime } = 3{u^2}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 3{u^2}.\left( { - 2\sin 2{\rm{x}}} \right) = 3{\left( {\cos 2{\rm{x}}} \right)^2}.\left( { - 2\sin 2{\rm{x}}} \right) = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
Vậy \(y' = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
c) Đặt \(u = \tan {\rm{x}}\) thì \(y = {u^2}\). Ta có: \(u{'_x} = {\left( {\tan {\rm{x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\) và \(y{'_u} = {\left( {{u^2}} \right)^\prime } = 2u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 2u.\frac{1}{{{{\cos }^2}x}} = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
Vậy \(y' = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
d) Đặt \(u = 4 - {x^2}\) thì \(y = \cot u\). Ta có: \(u{'_x} = {\left( {4 - {x^2}} \right)^\prime } = - 2{\rm{x}}\) và \(y{'_u} = {\left( {\cot u} \right)^\prime } = - \frac{1}{{{{\sin }^2}u}}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = - \frac{1}{{{{\sin }^2}u}}.\left( { - 2{\rm{x}}} \right) = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Vậy \(y' = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Đúng 0 Bình luận (0) Gửi Hủy 
- Nguyễn Hải Vân
Tìm đạo hàm các hàm số:
1, \(y=\tan(3x-\dfrac{\pi}{4})+\cot(2x-\dfrac{\pi}{3})+\cos(x+\dfrac{\pi}{6})\)
2, \(y=\dfrac{\sqrt{\sin x+2}}{2x+1}\)
3, \(y=\cos(3x+\dfrac{\pi}{3})-\sin(2x+\dfrac{\pi}{6})+\cot(x+\dfrac{\pi}{4})\)
Xem chi tiết Lớp 11 Toán Chương 5: ĐẠO HÀM 1 0 Gửi Hủy 
Nguyễn Việt Lâm CTV 22 tháng 3 2021 lúc 22:23 a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
Đúng 2 Bình luận (0) Gửi Hủy 
- Tài khoản bị khóa
Tính đạo hàm của các hàm số sau:
a) y=\(\dfrac{3x^2-18x-2}{1-2x}-\dfrac{2x-3}{x+4}\)
b) y=\(-\dfrac{\sin x}{3\cos^3x}+\dfrac{4}{3}\tan x\)
Xem chi tiết Lớp 11 Toán Bài 6: Ôn tập chương Đạo hàm 0 0 Gửi Hủy - Nguyễn Hải Vân
Tìm đạo hàm của các hàm số sau:
1, \(y=3^{(\dfrac{x}{\ln(x)})}\)
2, \(y=\dfrac{1}{2}tan^2(x)+\ln(tan(x))\)
3, 
\(y=\sqrt[3]{ln^2(2x)}\)
Gửi Hủy Nguyễn Việt Lâm CTV 9 tháng 9 2021 lúc 15:46 1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)
Đúng 1 Bình luận (2) Gửi Hủy - Pham Trong Bach
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy 
Cao Minh Tâm 
19 tháng 6 2018 lúc 6:49 Chọn D.
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
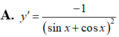
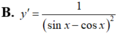
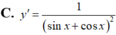
Gửi Hủy Cao Minh Tâm 20 tháng 7 2019 lúc 14:01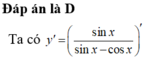 
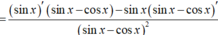
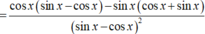
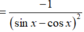
Gửi Hủy - Pham Trong Bach
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
Gửi Hủy Cao Minh Tâm 22 tháng 8 2019 lúc 17:00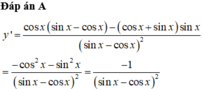 
Gửi Hủy - Giải mục 1 trang 95
-
a) Gọi \(g\left( x \right)\) có đạo hàm của hàm số \(y = \sin \left( {2x + \frac{\pi }{4}} \right).\) Tìm \(g\left( x \right)\).
b) Tính đạo hàm của hàm số \(y = g\left( x \right)\).
Xem chi tiết Lớp 11 Toán Bài 33. Đạo hàm cấp hai 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 22 tháng 9 2023 lúc 21:09 a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)
b) \(g'\left( x \right) = - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) = - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)
Đúng 0 Bình luận (0) Gửi Hủy Khoá học trên OLM (olm.vn)
- Toán lớp 11 (Kết nối tri thức với cuộc sống)
- Toán lớp 11 (Cánh Diều)
- Toán lớp 11 (Chân trời sáng tạo)
- Ngữ văn lớp 11
- Tiếng Anh lớp 11 (i-Learn Smart World)
- Tiếng Anh lớp 11 (Global Success)
- Vật lý lớp 11 (Kết nối tri thức với cuộc sống)
- Vật lý lớp 11 (Cánh diều)
- Hoá học lớp 11 (Kết nối tri thức với cuộc sống)
- Hoá học lớp 11 (Cánh diều)
- Sinh học lớp 11 (Kết nối tri thức với cuộc sống)
- Sinh học lớp 11 (Cánh diều)
- Lịch sử lớp 11 (Kết nối tri thức với cuộc sống)
- Lịch sử lớp 11 (Cánh diều)
- Địa lý lớp 11 (Kết nối tri thức với cuộc sống)
- Địa lý lớp 11 (Cánh diều)
- Giáo dục kinh tế và pháp luật lớp 11 (Kết nối tri thức với cuộc sống)
- Tin học lớp 11 (Kết nối tri thức với cuộc sống)
- Công nghệ lớp 11 (Kết nối tri thức với cuộc sống)
Từ khóa » đạo Hàm Tanx/sinx+2
-
Tính đạo Hàm Của Hàm Số Sau: \(y = {{\tan X} \over {\sin X + 2}}\)
-
Tìm Nguyên Hàm Sin(x)tan(x)^2 | Mathway
-
Tìm Đạo Hàm - D/dx Y=sin(x)^(tan(x)) | Mathway
-
Đạo Hàm Của Sinx^2 - Bảng Đạo Hàm Cơ Bản Và Nâng Cao Đầy ...
-
Tìm Các đạo Hàm 1. Y=tanx-sinx 2. Y=cos^5 2x 3. Y=cos4x.tanx 4. Y ...
-
Tính đạo Hàm Của Y=nx
-
Đạo Hàm Của Các Hàm Lượng Giác - Wikiwand
-
Chi Tiết Các Bước Cách Giải đạo Hàm Của Tan Là Gì? - Banhoituidap
-
Selfomy Hỏi Đáp
-
Giải Toán 11 Bài 3. Đạo Hàm Của Hàm Số Lượng Giác - Giải Bài Tập