Tìm điểm Cực Tiểu Của đồ Thị Hàm Số Y = X3 -3x2 -1

× Vui lòng đăng nhập để làm bài thi. Bạn chưa có tài khoản? Đăng ký ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 12 Toán

Câu hỏi:

16/11/2024 10,816

Tìm điểm cực tiểu của đồ thị hàm số y = x3-3x2-1?

A. (0;-2)

B. (0;1)

C. (5;-2)

D. (2;-5)

Đáp án chính xác Xem lời giải Câu hỏi trong đề: Trắc nghiệm Cực trị hàm số (có đáp án) Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Đáp án đúng: D.

*Lời giải

y'=3x2-6x; y'=0

⇔[x=0⇒yCĐ=-1x=2⇒yCT=-5

*Phương pháp giải:

Tính y'

Tìm nghiệm y' thay nghiệm vào y tìm CĐ CT

*Lý thuyết cần nắm và các dạng bài tập về cực trị hàm số:

- Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là −∞-∞; b là +∞+∞) và điểm x0∈∈(a; b).

a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và x≠x0x≠x0 thì ta nói hàm số f(x) đạt cực đại tại x0.

b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x∈∈(x0 – h; x0 + h) và x≠x0x≠x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.

Điều kiện đủ để hàm số có cực trị

- Định lí 1

Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0– h; x0+ h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.

a) Nếu f’(x) > 0 trên khoảng (x0– h; x0) và f’(x) < 0 trên khoảng (x0; x0+ h) thì x0là một điểm cực đại của hàm số f(x).

b) Nếu f’(x) < 0 trên khoảng (x0– h; x0) và f’(x) > 0 trên khoảng (x0; x0+ h) thì x0là một điểm cực tiểu của hàm số f(x).

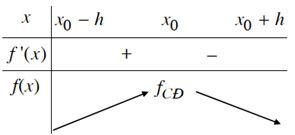
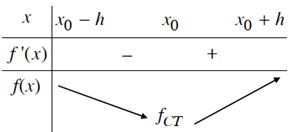
Quy tắc tìm cực trị.

- Quy tắc 1.

1. Tìm tập xác định.

2. Tính f’(x). Tìm các điểm tại đó f’(x) bằng 0 hoặc f’(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

- Định lí 2.

Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x0– h; x0+ h) với h > 0. Khi đó:

a) Nếu f’(x0) = 0; f”(x0) > 0 thì x0là điểm cực tiểu;

b) Nếu f’(x0) = 0; f”(x0) < 0 thì x0là điểm cực đại.

- Quy tắc II.

1. Tìm tập xác định

2. Tính f’(x). Giải phương trình f’(x) = 0 và kí hiệu xi( i = 1; 2; ….; n) là các nghiệm của nó.

3. Tính f”(x) và f”(xi).

4. Dựa vào dấu của f”(xi) suy ra tính chất cực trị của điểm xi.

Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y=ax3+bx2+cx+d (a≠0).

- Ta có y'=3ax2+2bx+c

Đồ thị hàm số có 2 điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt .

⇔b2−3ac>0

Và không có cực trị ⇔Δ’ = b2 − 3ac ≤ 0

- Cho hàm số y=ax3+bx2+cx+d có hai điểm cực trị phân biệt là A, B . Khi đó:

Phương trình đường thẳng AB : y = 23(c -2b3a )x + (d -bc9a)

Độ dài đoạn thẳng AB = 4e+ 16e3a với e = b2−3ac9a

Hoặc khi đó đường thẳng qua hai điểm cực trị liên quan tới: y−y'.y''18a (CASIO hỗ trợ).

Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.

Cho hàm số:y=ax4+bx2+c (a≠0) có đồ thị là (C) .

Ta cóy'=4ax3+2bx; 

 y'=0⇔x=0x2=−b2a

(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt⇔−b2a>0hay ab < 0

Hàm số có 3 cực trị là:

A(0;c),B−−b2a;−Δ4a,C−b2a;−Δ4a.

Độ dài các đoạn thẳng:

AB=AC=b416a2−b2a  ,  BC=2−b2a

CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Tìm các điểm cực trị của hàm số.

Quy tắc 1: Áp dụng định lý 2

- Tìm f’(x)

- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm

- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo

Quy tắc 2: Áp dụng định lý 3

- Tìm f’(x)

- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0

- Với mỗi xi tính f ”(xi)

- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi

- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi

Dạng 2: Tìm điều kiện để hàm số có cực trị.

Sử dụng định lí 2 và định lí 3

a, Cực trị của hàm số bậc ba:

Cho hàm số y = ax3+ bx2+ cx + d, a ≠ 0.

y’ = 0 ⇔ 3ax2+ 2bx + c = 0 (1) ; Δ’y’= b2– 3ac

- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

→ Hàm số bậc 3 không có cực trị ⇔ b2– 3ac ≤ 0

- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

→ Hàm số bậc 3 có 2 cực trị ⇔ b2– 3ac > 0

b, Cực trị của hàm số bậc bốn trùng phương:

Cho hàm số: y = ax4+ bx2+ c (a ≠ 0) có đồ thị là (C).

y' = 4ax3+ 2bx; y' = 0

⇔x=0x2=−b2a

- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Chú ý

* Hàm sốf(xác định trên D) có cực trị ⇔ ∃xo∈ D thỏa mãn hai điều kiện sau:

- Tại đạo hàm của hàm số tạixophải bằng 0 hoặc hàm số không có đạo hàm tạixo

- f ‘(x)phải đổi dấu qua điểmxohoặcf ”(xo) ≠ 0.

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12

Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất

TOP 40 câu Trắc nghiệm Cực trị hàm số (có đáp án 2024) - Toán 12

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm giá trị cực đại yCĐcủa hàm số y = x3- 3x +2

Xem đáp án » 02/12/2024 48,254

Câu 2:

Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?

Xem đáp án » 23/07/2024 15,101

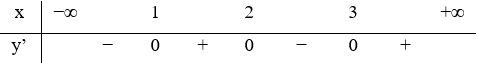
Câu 3:

Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.

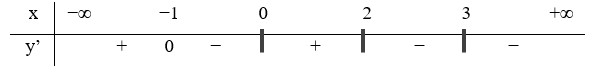
Hỏi hàm số có bao nhiêu điểm cực trị?

Xem đáp án » 23/07/2024 11,444

Câu 4:

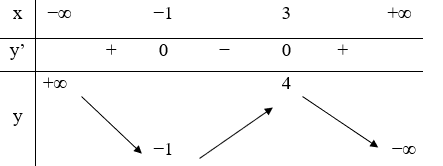
Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm

Xem đáp án » 23/07/2024 7,387

Câu 5:

Đồ thị của hàm số y = -x3+ 3x +5 có hai điểm cực trị A và B. Tính diện tíchScủa tam giácOABvớiOlà gốc tọa độ.

Xem đáp án » 23/07/2024 5,787

Câu 6:

Cho hàm số y=f(x) có bảng biến thiên như sau

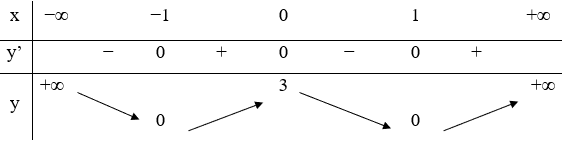
Mệnh đề nào dưới đâysai?

Xem đáp án » 23/07/2024 4,836

Câu 7:

Biết hàm số (C): y=13x3-32x2+2x+1có hai điểm cực trị là x1,x2.Đẳng thức nào sau đây đúng?

Xem đáp án » 23/07/2024 3,051

Câu 8:

Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau

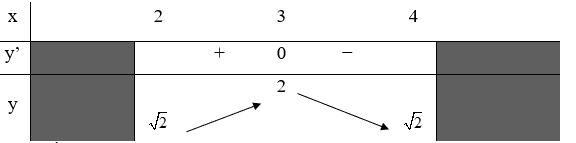
Mệnh đề nào sau đây đúng?

Xem đáp án » 23/07/2024 2,336

Câu 9:

Cho hàm số y = f(x) có đạo hàm f'(x) = x2019(x2020- 1), ∀x∈R. Hỏi hàm số có bao nhiêu điểm cực trị?

Xem đáp án » 11/10/2024 2,148

Câu 10:

Tổng các điểm cực trị của hàm sốy=13x3-52x2+6x-1 bằng

Xem đáp án » 23/07/2024 2,134

Câu 11:

Hàm số y=f(x) liên tục trênR\ {3} và có bảng xét dấu đạo hàm như hình vẽ.

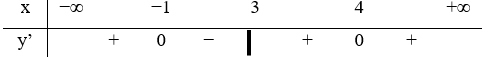
Số điểm cực trị của hàm số y = g(x) = f(x2+2x+3) là

Xem đáp án » 23/07/2024 1,261

Câu 12:

Tích các điểm cực trị của hàm sốy= 13x3+4x2-9x-2026 bằng:

Xem đáp án » 23/07/2024 1,028

Câu 13:

Hàm số y =f(x) liên tục trên R|{0}và có bảng biến thiên như hình vẽ.

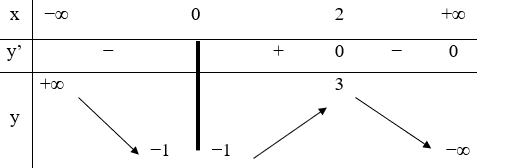
Khẳng định nào sau đây là khẳng định đúng?

Xem đáp án » 16/07/2024 885

Câu 14:

Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

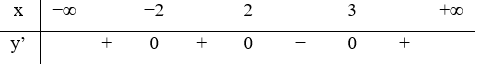
Số điểm cực trị của hàm số y=g(x)=f(1-x2) là

Xem đáp án » 23/07/2024 787

Câu 15:

Đồ thị của hàm số y = x3- 3x2- 9x +1 có hai điểm cực trịAvàB. Điểm nào dưới đây thuộc đường thẳng AB?

Xem đáp án » 17/07/2024 728 Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

• Top 8 Đề kiểm tra Toán 12 Chương 1 Hình học có đáp án 8 đề 4,731 lượt thi Thi thử
• Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án 4 đề 3,693 lượt thi Thi thử
• Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải 10 đề 3,623 lượt thi Thi thử
• Bài tập Tích phân ôn thi Đại học có lời giải 10 đề 3,594 lượt thi Thi thử
• Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án 9 đề 3,484 lượt thi Thi thử
• Top 8 Đề kiểm tra Toán 12 Chương 2 Hình học có đáp án 8 đề 3,472 lượt thi Thi thử
• 261 Bài tập trắc nghiệm Hình học Mặt nón, mặt trụ, mặt cầu cực hay có lời giải chi tiết 9 đề 3,375 lượt thi Thi thử
• 200 Bài tập nguyên hàm tích phân cơ bản, nâng cao 9 đề 3,205 lượt thi Thi thử
• Top 8 Đề kiểm tra Toán 12 Chương 2 Giải tích có đáp án 8 đề 3,177 lượt thi Thi thử
• Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án 8 đề 3,144 lượt thi Thi thử

Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

• 

  Viết phương trình mặt cầu (S) biết (S) qua bốn điểm A(1;2;-4); B(1;-3;1); C(2;2;3) và D(1;0;4).

  871 18/07/2024 Xem đáp án
• 

  Mặt cầu (S): x2 + y2 + z2 - 4x + 1 = 0 có tọa độ tâm và bán kính R là:

  497 23/07/2024 Xem đáp án
• 

  Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆1: x+13=y-21=z-12 và ∆2: x-11=y2=z+13. Phương trình đường thẳng ∆ song song với d: x=3y=-1+tz=4+t và cắt hai đường thẳng Δ1; Δ2 là:

  521 17/07/2024 Xem đáp án
• 

  Cho hai đường thẳng d1: x=2+ty=-1+tz=3 và d2: x=1-ty=2z=-2+t. Góc giữa hai đường thẳng d1 và d2 là:

  475 21/07/2024 Xem đáp án
• 

  Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(-1;3;2); B(2;0;5); C(0;-2;1). Phương trình đường trung tuyến AM của tam giác ABC là.

  561 23/07/2024 Xem đáp án
• 

  Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x+22=y-1-1=z-33. Đường thẳng d đi qua điểm M và có vectơ chỉ phương αd→ có tọa độ là:

  461 22/07/2024 Xem đáp án
• 

  Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (α): 3x + (m - 1)y + 4z - 2 = 0, (β): nx + (m + 2)y + 2z + 4 = 0. Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β)

  592 20/07/2024 Xem đáp án
• 

  Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x + 2y - 2z + 1 = 0 và cách (Q) một khoảng bằng 3.

  891 18/07/2024 Xem đáp án
• 

  Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(-1;-2;5) và vuông góc với hai mặt phẳng (Q): x + 2y - 3z + 1 = 0 và (R): 2x - 3y + z + 1 = 0.

  601 20/07/2024 Xem đáp án
• 

  Trong không gian Oxyz, viết phương trình mặt phẳng đi qua ba điểm A(1;0;-2), B(1;1;1), C(0;-1;2).

  666 20/07/2024 Xem đáp án

Xem thêm »