Tìm Họ Nguyên Hàm Của Hàm Số F( X )=2018x - Sách Toán - Học Toán

Trang chủ » Nguyên Hàm Sin 2018 X » Tìm Họ Nguyên Hàm Của Hàm Số F( X )=2018x - Sách Toán - Học Toán

Có thể bạn quan tâm

  • Skip to main content
  • Skip to secondary menu
  • Bỏ qua primary sidebar
Bạn đang ở:Trang chủ / Trắc nghiệm Nguyên hàm / Tìm họ nguyên hàm của hàm số f( x )=2018x

Câu hỏi: Tìm họ nguyên hàm của hàm số f( x )=2018x

A. \( \frac{{{{2018}^x}}}{{\log 2018}} + C.\) B. \( \frac{{{{2018}^{x\, + \,1}}}}{{x + 1}} + C.\) C. \( \frac{{{{2018}^x}}}{{\ln 2018}} + C.\) D. \( 2018^x.ln2018+C.\)

Lời Giải: Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 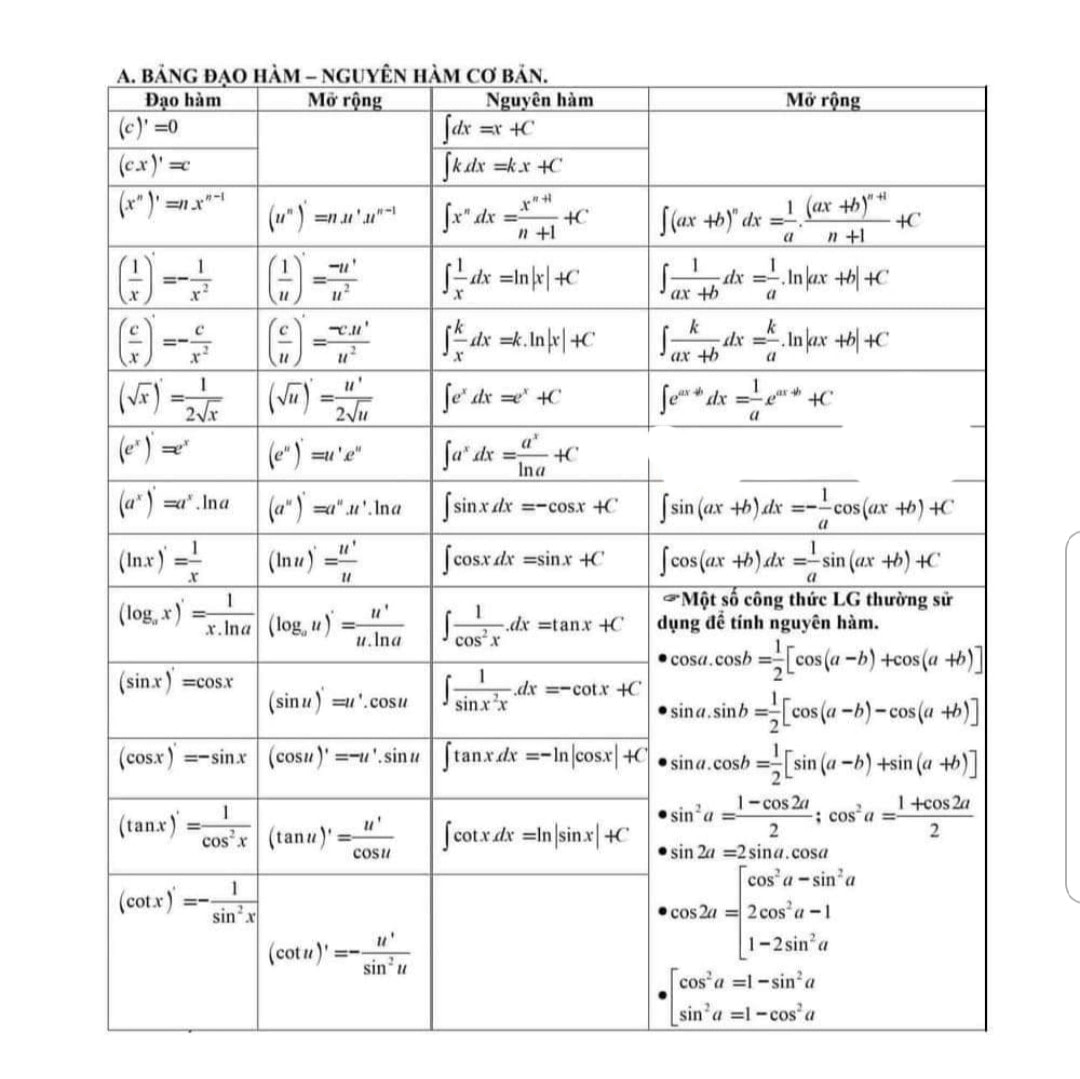Tìm họ nguyên hàm của hàm số f( x )=2018x 1

Ta có

\( \smallint f\left( x \right){\mkern 1mu} {\rm{d}}x = \smallint {2018^x}{\mkern 1mu} {\rm{d}}x = \frac{{{{2018}^x}}}{{\ln 2018}} + C.\)

===============

==================== Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Để lại một bình luận Hủy

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

Bình luận *

Tên *

Email *

Trang web

Δ

Sidebar chính

Nhập từ cần tìm ...

MỤC LỤC

Từ khóa » Nguyên Hàm Sin 2018 X