Tìm M để Hàm Số Có Cực đại, Cực Tiểu (xác định M để ... - Hayhochoi

I. Phương pháp chung tìm cực trị của hàm số

• Để thực hiện các yêu cầu về điều kiện có cực trị của hàm số y=f(x) ta thực hiện theo các bước:

- Bước 1: Tìm miền xác định D.

- Bước 2: Tính đạo hàm y'.

- Bước 3: Lựa chọn theo một trong 2 cách sau:

+) Cách 1: Nếu xét được dấu của y' thì:

 Hàm số có k cực trị ⇔ Phương trình y'=0 có k nghiệm phân biệt và y' đổi dấu qua các nghiệm đó.

+) Cách 2: Nếu không xét được dấu của y' hoặc bài toán yêu cầu cụ thể về cực đại hoặc cực tiểu thì ta tính thêm y''. Khi đó:

i) Hàm số có cực trị ⇔ Hệ sau có nghiệm thuộc D: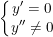 

ii) Hàm số có cực tiểu ⇔ Hệ sau có nghiệm thuộc D: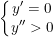 

iii) Hàm số có cực đại ⇔ Hệ sau có nghiệm thuộc D: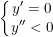 

II. Bài tập, ví dụ minh họa

Bài tập 1: Tìm m để hàm số y = (m - 1)x3 - 3x2 - (m + 1)x + 3m2 - m + 2 có cực đại và cực tiểu.

Lời giải:

- TXĐ: D = R

- y' = 3(m - 1)x2 - 6x - (m + 1)

Cho y' = 0 ⇔ 3(m - 1)x2 - 6x - (m + 1) = 0

Để hàm số có cực đại và cực tiểu thì: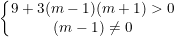

 

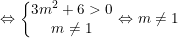
Vậy với m≠1 thì hàm số có cực đại, cực tiểu.

Bài tập 2: Xác định m để hàm số sau có 3 điểm cực trị: y = mx4 - (m + 1) x2 + 2m - 1.

Lời giải:

- TXĐ: D = R

- Ta có: y' = 4mx3 - 2(m + 1)x = 0

 ⇔ x[4mx2 - 2(m + 1)] = 0

 ⇔ x = 0 hoặc 2mx2 = m + 1

Hàm số có 3 điểm cực trị khi và chỉ khi: 2mx2 = m + 1 có 2 nghiệm

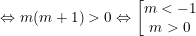
Kết luận: Vậy hàm số có 3 cực trị khi và chỉ khi m<-1 hoặc m>0.

Bài tập 3: Cho hàm số: y = x3 - 2(m + 1)x2 + (m2 - 3m + 2)x + 4  (*). Xác định m để hàm số (*) có cực đại và cực tiểu nằm về 2 phía của trục tung.

Lời giải:

- TXĐ: D = R

- Ta có y' = 3x2 - 2(2m + 1)x + m2 - 3m + 2

- Hàm số đạt cực đại, cực tiểu nằm về 2 phía của trục tung khi và chỉ khi y' = f'(x) = 0 có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < 0 < x2 (khi đó c/a của pt bậc 2 trái dấu):

  

 

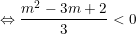
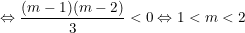
Vậy với 1<m<2 thì hàm số trên có cực đại và cực tiểu nằm về hai phía đối với trục tung.

Bài tập 4: Cho hàm số   (*)

Tìm α để hàm số có cực đại, cực tiểu thoả: yCĐ + yCT = -6.

Lời giải:

- TXĐ: R\{-1}

- Ta có: 

⇔ x2 + 2x + sinα - |sinα| + 1 = 0  (1)

Δ = 4 - 4(sinα - |sinα| + 1) = 4(|sinα| - sinα)

Điều kiện để hàm số có cực đại và cực tiểu là: 

Với Δ > 0 ⇔ |sinα| - sinα > 0

 ⇔ sinα < 0 

 ⇔ (2k + 1)π < α < (k + 1)2π (k ∈ Z) (2)

- Theo bài ra: yCĐ + yCT = -6

- Từ (*) khi sinα < 0, ta có:

 

  

nên yCĐ + yCT = -6:

⇔ 2(xCĐ + xCT) + 2sinα = -6

(xCĐ, xCT là 2 nghiệm của (1) nên xCĐ + xCT = -2)

 ⇔ 2.(-2) + 2sinα = -6 ⇔ sinα = -1

 

Thoả điều kiện (2), do đó:

 thì hàm số có cực đại, cực tiểu thoả yCĐ + yCT = -6.