Tìm M để Hàm Số đạt Cực Trị
Có thể bạn quan tâm
CỰC TRỊ CỦA HÀM BẬC 3
Bài toán tổng quát: Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số). Tìm giá trị của tham số để hàm số có cực đại, cực tiểu (cực trị) thỏa mãn điều kiện cho trước.
Phương pháp:
Bước 1: Tính y’ = 3ax2 + 2bx + c, y’ = 0 ⇔ 3ax2 +2bx + c = 0 (1)
Để hàm số có cực đại, cực tiểu ⇔ y’ = 0 có hai nghiệm phân biệt ⇔ (1) có hai nghiệm phân biệt
\(\left\{\begin{matrix} a\neq 0 & \\ \Delta (\Delta ')\neq 0 & \end{matrix}\right.\)⇔ Giá trị tham số thuộc miền D nào đó (*)
Bước 2:
Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.
Một số điều kiện thường gặp:
- Để hàm số y = f(x) có 2 cực trị <=> \(\left\{\begin{matrix} a\neq 0 & \\ \Delta _{y'}>0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục hoành <=> \(y_{CD}.y_{CT}<0\)
- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục tung <=> \(x_{CD}.x_{CT}<0\)
- Để hàm số y = f(x) có 2 cực trị nằm phía trên trục hoành <=> \(\left\{\begin{matrix} y_{CD}+y_{CT}>0 & \\ y_{CD}.y_{CT}>0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có 2 cực trị nằm phía dưới trục hoành <=> \(\left\{\begin{matrix} y_{CD}+y_{CT} <0& \\ y_{CD}.y_{CT}<0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có cực trị tiếp xúc với trục hoành <=> \(y_{CD}.y_{CT}=0\)
- Đồ thị có 2 điểm cực trị khác phía đối với đường thẳng d: Ax +By +C = 0

Chú ý: Khi thay đường thẳng d bằng trục Ox hoặc Oy hoặc một đường tròn thì vẫn áp dụng kết quả trên . Các kết quả khác thì tùy từng điều kiện để áp dụng.
VÍ DỤ MINH HỌA
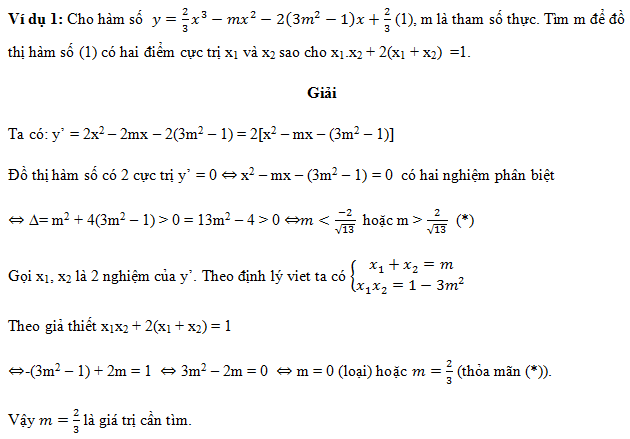

Từ khóa » Tìm M để Hàm Số Có 2 Cực Trị Dương
-
Tìm M để Hàm Số Có Cực Trị (hàm Số đa Thức Bậc 3) - Toán Thầy Định
-
Tìm M để Hàm Bậc Ba Có 2 điểm Cực Trị Cực Hay, Có Lời Giải
-
Tìm M để Hàm Số Có Cực Trị Thỏa Mãn điều Kiện Cho Trước (PDF)
-
Tổng Hợp Tìm M để Hàm Số Có 2 điểm Cực Trị - Banmaynuocnong
-
I. CỰC TRỊ CỦA HÀM SỐ BẬC BA LÀ GÌ - THPT Sóc Trăng
-
Tìm M để Hàm Bậc Ba Có 2 điểm Cực Trị Cực Hay, Có Lời Giải - Haylamdo
-
Dạng Bài Tìm M để Hàm Số Có Cực Trị Thỏa Mãn - .vn
-
Bài 3: MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ
-
[TOAN 12] – Tìm M để Hàm Số Có Hai điểm Cực Trị Nằm Khác Phía Và ...
-
Tìm M để Hàm Số Có Hai điểm Cực Trị Nằm Khác Phía Và Cách đều ...
-
Tổng Hợp Tìm M Để Hàm Số Có Cực Đại Và Cực Tiểu Thỏa Điều Kiện
-
Tìm điều Kiện để Hàm Số Bậc Ba Có Cực Trị Hoặc Không Có Cực Trị
-
Tìm điều Kiện để Hàm Số Bậc 3 Có Cực Trị Thỏa Mãn điều Kiện Cho Trước
-
Tìm điều Kiện để Hàm Số Trùng Phương Có Cực Trị ...