Tìm Nguyên Hàm Của Hàm Số: F(x)=cos2x(sin^4 X+cos^4 X)

Tất cả Toán học Vật Lý Hóa học Văn học Lịch sử Địa lý Sinh học Giáo dục công dân Tin học Tiếng anh Công nghệ Khoa học Tự nhiên Lịch sử và Địa lý Hoàng Bách đã hỏi trong Lớp 12 Toán học · 09:22 29/08/2020 Chương 3: Nguyên hàm - Tích phân và ứng dụng Theo dõi Báo cáo

Tìm nguyên hàm của hàm số: fx=cos2xsin4x+cos4x.

Trả Lời Hỏi câu khác Hỏi chi tiết ...Xem thêm

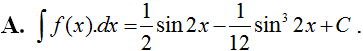
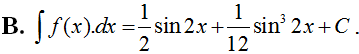
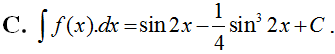
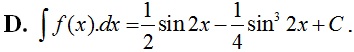
Quảng cáo

1 câu trả lời 397

Quang Minh 5 năm trước

Chọn A

0 bình luận Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?

Đặt câu hỏi

Câu hỏi hot cùng chủ đề

• ∫lncosxcos2xdx