Tìm Nguyên Hàm Của Hàm Số (f(x)=sqrt{x} Ln X). - Sách Toán - Học Toán

Trang chủ » Nguyên Hàm Của Căn X Lnx Dx » Tìm Nguyên Hàm Của Hàm Số (f(x)=sqrt{x} Ln X). - Sách Toán - Học Toán

Có thể bạn quan tâm

  • Skip to main content
  • Skip to secondary menu
  • Bỏ qua primary sidebar
Bạn đang ở:Trang chủ / Trắc nghiệm Nguyên hàm / Tìm nguyên hàm của hàm số \(f(x)=\sqrt{x} \ln x\).

Câu hỏi: Tìm nguyên hàm của hàm số \(f(x)=\sqrt{x} \ln x\).

A. \(\int f(x) \mathrm{d} x=\frac{1}{9} x^{\frac{3}{2}}(3 \ln x-2)+C\) B. \(\int f(x) \mathrm{d} x=\frac{2}{3} x^{\frac{3}{2}}(3 \ln x-2)+C\) C. \(\int f(x) \mathrm{d} x=\frac{2}{9} x^{\frac{3}{2}}(3 \ln x-1)+C\) D. \(\int f(x) \mathrm{d} x=\frac{2}{9} x^{\frac{3}{2}}(3 \ln x-2)+C\)

Lời Giải: Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 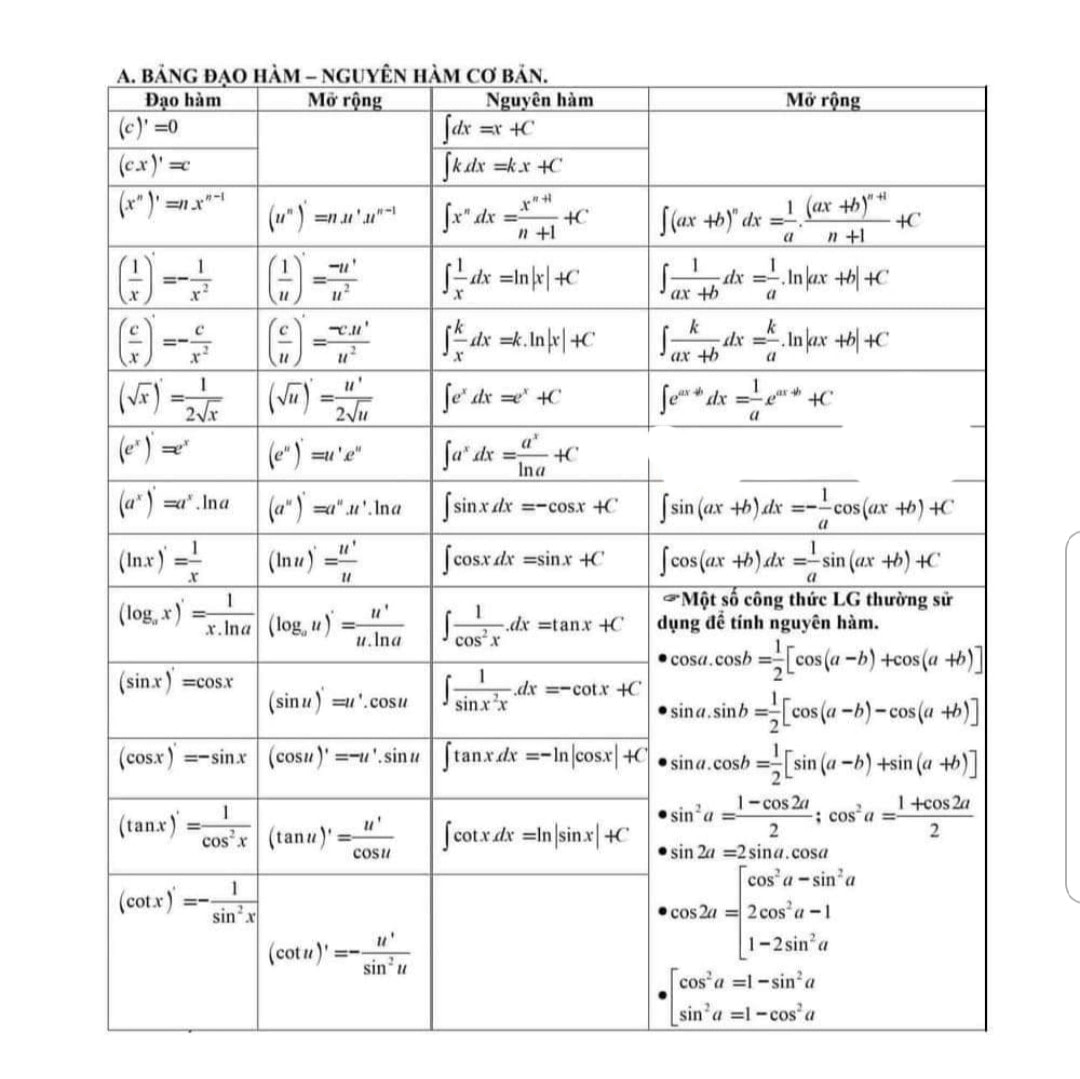Tìm nguyên hàm của hàm số (f(x)=sqrt{x} ln x). 1

\(I=\int f(x) \mathrm{d} x=\int \sqrt{x} \ln x \cdot \mathrm{d} x\)

\(\begin{array}{l} \text { Đăt: } t=\sqrt{x} \Rightarrow \mathrm{d} t=\frac{1}{2 \sqrt{x}} \mathrm{d} x \Rightarrow 2 t \mathrm{d} t=\mathrm{d} x \\ \Rightarrow I=2 \int t^{2} \ln t^{2} \cdot \mathrm{d} t=4 \int t^{2} \ln t \cdot \mathrm{d} t \end{array}\)

\(\text { Đặt: }\left\{\begin{array}{l} u=\ln t \\ \mathrm{d} v=t^{2} \mathrm{d} t \end{array} \Rightarrow\left\{\begin{array}{l} \mathrm{d} u=\frac{1}{t} \mathrm{d} t \\ v=\frac{t^{3}}{3} \end{array}\right.\right.\)

\(\begin{array}{l} \Rightarrow I=2\left(\frac{1}{3} t^{3} \ln t-\frac{1}{3} \int t^{2} \mathrm{d} t\right)=2\left(\frac{1}{3} t^{3} \ln t-\frac{1}{9} t^{3}+C\right)\\ =\frac{2}{9} t^{3}(3 \ln t-1)+C \\ =\frac{2}{9} x^{\frac{3}{2}}(3 \ln \sqrt{x}-1)+C \\ =\frac{1}{9} x^{\frac{3}{2}}(3 \ln x-2)+C \end{array}\)

 

===============

==================== Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Để lại một bình luận Hủy

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

Bình luận *

Tên *

Email *

Trang web

Δ

Sidebar chính

Nhập từ cần tìm ...

MỤC LỤC

Từ khóa » Nguyên Hàm Của Căn X Lnx Dx