Tìm Nguyên Hàm (I=int(x-1) Sin 2 Xdx) - Sách Toán

Trang chủ » Nguyên Hàm Của 1/sin^2(2x) » Tìm Nguyên Hàm (I=int(x-1) Sin 2 Xdx) - Sách Toán

Có thể bạn quan tâm

  • Skip to main content
  • Skip to secondary menu
  • Bỏ qua primary sidebar
Bạn đang ở:Trang chủ / Trắc nghiệm Nguyên hàm / Tìm nguyên hàm \(I=\int(x-1) \sin 2 x d x\)

Câu hỏi: Tìm nguyên hàm \(I=\int(x-1) \sin 2 x d x\)

A. \(I=\frac{(1-2 x) \cos 2 x+\sin 2 x}{2}+C\) B. \(I=\frac{(2-2 x) \cos 2 x+\sin 2 x}{2}+C\) C. \(I=\frac{(1-2 x) \cos 2 x+\sin 2 x}{4}+C\) D. \(I=\frac{(2-2 x) \cos 2 x+\sin 2 x}{4}+C\)

Lời Giải: Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 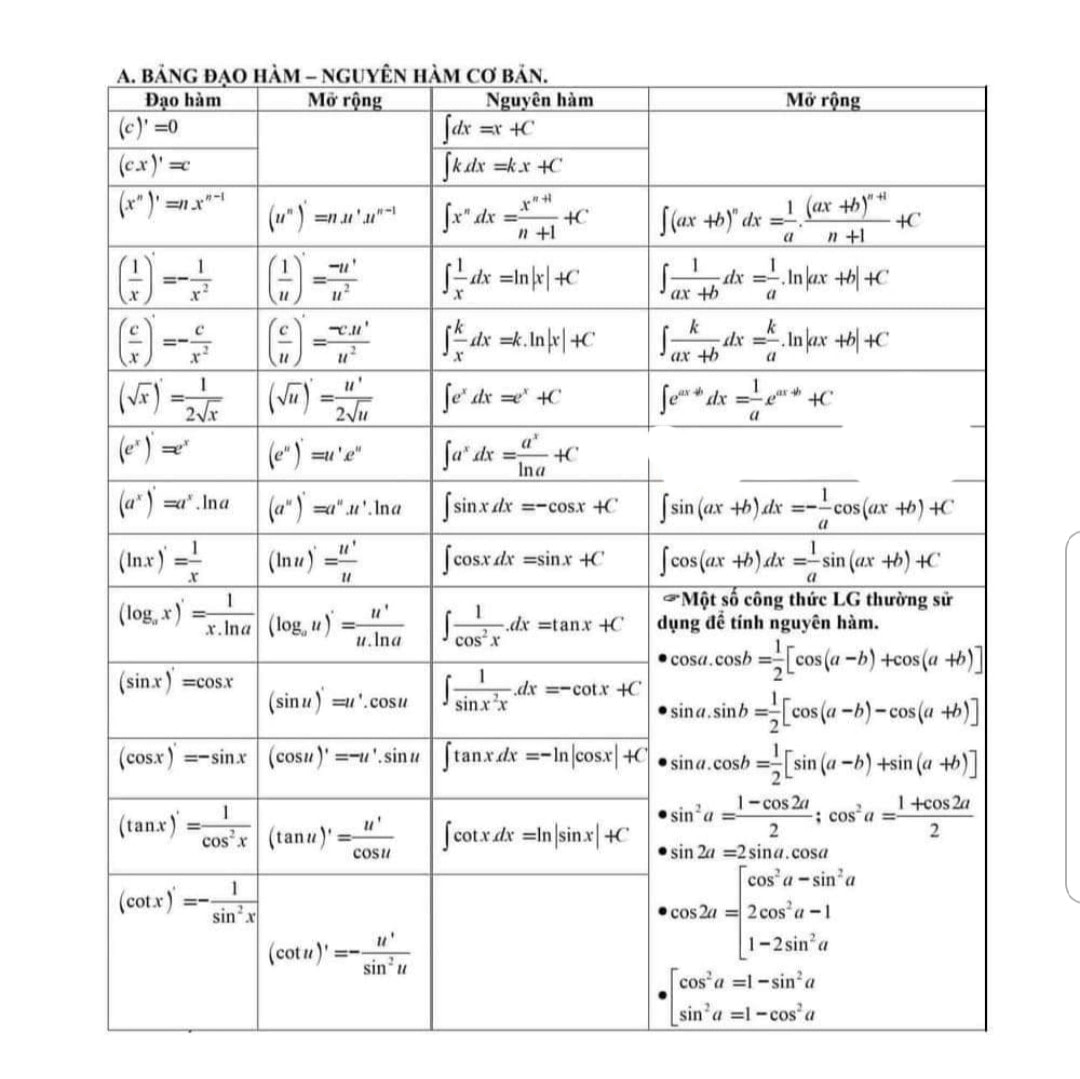Tìm nguyên hàm (I=int(x-1) sin 2 x d x) 1

Đặt \(\left\{\begin{array}{l} u=x-1 \\ \mathrm{d} v=\sin 2 x \mathrm{d} x \end{array} \Rightarrow\left\{\begin{array}{l} \mathrm{d} u=\mathrm{d} x \\ v=-\frac{1}{2} \cos 2 x \end{array}\right.\right.\)

Khi đó :

\(I=\int(x-1) \sin 2 x \mathrm{d} x=-\frac{1}{2}(x-1) \cos 2 x+\frac{1}{2} \int \cos 2 x \mathrm{d} x\\ =-\frac{1}{2}(x-1) \cos 2 x+\frac{1}{4} \sin 2 x+C\\ =\frac{(2-2 x) \cos 2 x+\sin 2 x}{4}+C\)

===============

==================== Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Reader Interactions

Để lại một bình luận Hủy

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

Bình luận *

Tên *

Email *

Trang web

Δ

Sidebar chính

Nhập từ cần tìm ...

MỤC LỤC

Từ khóa » Nguyên Hàm Của 1/sin^2(2x)