Tính Chất Tứ Diện đều

Tứ diện đều Tính chất tứ diện đều Bài trước Tải về Bài sau Lớp: Lớp 11 Môn: Toán Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Tứ diện đều

• 1. Tứ diện
• 2. Tứ diện đều
• 3. Tính chất tứ diện đều
• 4. Cách vẽ tứ diện đều
• 5. Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng
• 5. Thể tích tứ diện đều
• 6. Công thức tính nhanh thể tích tứ diện đều cạnh a
• 7. Ứng dụng thực tế của tứ diện đều
• 8. Bài tập tính thể tích khối tứ diện đều

Bạn đang tìm hiểu về tứ diện đều trong hình học không gian? Đây là một trong những khối đa diện đặc biệt, thường xuyên xuất hiện trong chương trình Hình học lớp 11 cũng như các đề thi học kỳ, đề thi đại học. Bài viết “Tứ diện đều” dưới đây sẽ giúp bạn nắm rõ khái niệm, đặc điểm hình học, công thức tính toán liên quan và đặc biệt là tổng hợp tính chất tứ diện đều một cách đầy đủ, khoa học và dễ hiểu. Với hệ thống kiến thức chuẩn và ví dụ minh họa, bạn sẽ dễ dàng áp dụng vào bài tập và nâng cao tư duy hình học không gian của mình.

1. Tứ diện

• Tứ diện là hình có bốn đỉnh, thường được kí hiệu A, B, C, D. Bất kì điểm nào trong số các điểm trên được gọi là đỉnh, mặt tam giác đối diện với đỉnh đó được gọi là đáy. 
• Ví dụ: Chọn A là đỉnh thì (BCD) là mặt đáy.

2. Tứ diện đều

• Tứ diện đều là tứ diện có 4 mặt là tam giác đều.
• Tứ diện đều là một hình chóp tam giác đều.
• Hình chóp tam giác đều có thêm điều kiện cạnh bên bằng cạnh đáy là tứ diện đều.

Hình vẽ minh họa tứ diện đều

3. Tính chất tứ diện đều

- Tứ diện đều có các tính chất như sau:

• Bốn mặt xung quanh là các tam giác đều bằng nhau.
• Các mặt của tứ diện là những tam giác có ba góc đều nhọn.
• Tổng các góc tại một đỉnh bất kì của tứ diện là 1800.
• Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau.
• Tất cả các mặt của tứ diện đều tương đương nhau.
• Bốn đường cao của tứ diện đều có độ dài bằng nhau.
• Tâm của các mặt cầu nội tiếp và ngoại tiếp nhau, trùng với tâm của tứ diện.
• Hình hộp ngoại tiếp tứ diện là hình hộp chữ nhật.
• Các góc phẳng nhị diện ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau.
• Đoạn thẳng nối trung điểm của các cạnh đối diện là một đường thẳng đứng vuông góc của cả hai cạnh đó.
• Một tứ diện có ba trục đối xứng.
• Tổng các cos của các góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1.

4. Cách vẽ tứ diện đều

Để giải các bài toán hình học không gian liên quan đến tứ diện đều, việc vẽ chính xác hình tứ diện là bước khởi đầu rất quan trọng. Một hình tứ diện đều được xây dựng như sau:

Bước 1: Xác định hình chóp tam giác đều

Hình tứ diện đều có thể được hình dung như một hình chóp tam giác đều với đỉnh A và mặt đáy là tam giác BCD.

Bước 2: Vẽ mặt đáy tam giác BCD

Bắt đầu bằng cách vẽ tam giác BCD, đảm bảo rằng đây là một tam giác đều.

Bước 3: Tìm trọng tâm của tam giác đáy

Dựng các đường trung tuyến của tam giác BCD để xác định trọng tâm G, điểm giao của các đường trung tuyến.

Bước 4: Dựng đường cao của hình

Từ trọng tâm G của tam giác BCD, dựng một đường thẳng vuông góc với mặt phẳng chứa tam giác BCD. Đây chính là đường cao của hình tứ diện.

Bước 5: Định vị đỉnh A

Chọn đỉnh A trên đường cao vừa dựng sao cho khoảng cách từ A đến mặt phẳng đáy BCD đảm bảo tứ diện đều (thường dựa vào bài toán hoặc mô hình).

Bước 6: Hoàn thiện các cạnh

Nối đỉnh A với các đỉnh B, C, D của tam giác đáy. Bạn sẽ thu được một hình tứ diện đều hoàn chỉnh.

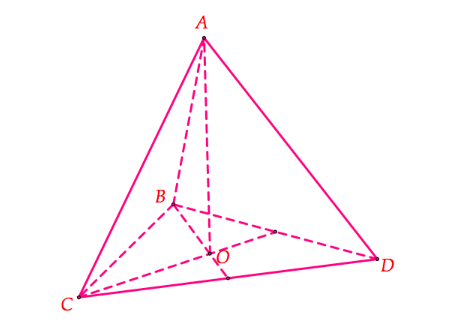
5. Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng

Các mặt phẳng đối xứng của tứ diện đều là:

• Các mặt của tứ diện đều.
• Các mặt phẳng chứa một cặp cạnh đối diện và đi qua trung điểm của cạnh thứ ba.
• Mặt phẳng song song với mặt đó và đi qua trọng tâm của tứ diện đều.

Có thể phân loại các mặt phẳng đối xứng của tứ diện đều như sau:

• Mặt phẳng đối xứng chính là các mặt phẳng chứa các cạnh của tứ diện đều. Có 4 mặt phẳng đối xứng chính, tương ứng với 4 mặt của tứ diện đều.
• Mặt phẳng đối xứng phụ là các mặt phẳng không chứa cạnh nào của tứ diện đều. Có 6 mặt phẳng đối xứng phụ, tương ứng với 6 cặp mặt đối diện của tứ diện đều.

Chúng ta xem hình sau thì sẽ hiểu rõ về 6 mặt phẳng đối diện nhau của hình tứ diện đều:

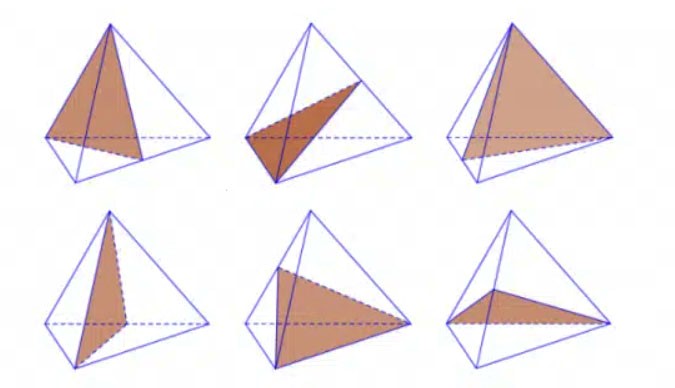
5. Thể tích tứ diện đều

- Một tứ diện đều sẽ có 6 cạnh bằng nhau và 4 mặt tam giác đều sẽ có các công thức tính thể tích tứ diện

Thể tích tứ diện ABCD

Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng:

\(V=\dfrac{1}{3}.S_{BCD}.AH\)Thể tích tứ diện đều tam giác S.ABC

Thể tích của một khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đó:

\(V=\dfrac{1}{3}.B.h\)

6. Công thức tính nhanh thể tích tứ diện đều cạnh a

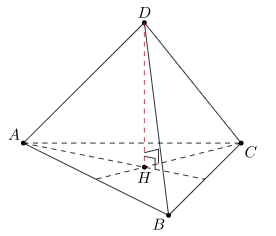
Cho tứ diện đều ABCD cạnh a. từ A kẻ AH là đường cao của hình chóp A.BCD, H thuộc (BCD) thì H sẽ là tâm của tam giác đều BCD. Suy ra 

• Chiều cao của hình chóp A.BCD đều cạnh a là \(h = AH=\frac{a\sqrt{6}}{3}\)
• Thể tích khối tứ diện đều cạnh a là \(V=\frac{a^3\sqrt{2}}{12}\)

Chứng minh 

Hình vẽ minh họa

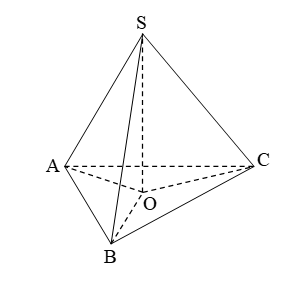
Gọi tứ diện \(ABCD\) đều cạnh \(a\).

Gọi \(H\) là hình chiếu của \(A\) lên \((BCD)\).

Ta có: \(BH = \frac{a\sqrt{3}}{3}\)

\(\Rightarrow AH = \sqrt{AB^{2} - BH^{2}} = \frac{a\sqrt{6}}{3}\)

\(S_{\Delta BCD} = \frac{a^{2}\sqrt{3}}{4}\) \(\Rightarrow V_{ABCD} = \frac{a^{3}\sqrt{2}}{12}\).

Ví dụ 1. Giả sử \(V\) là thể tích khối tứ diện đều \(ABCD\). Trung điểm tất cả các cạnh của tứ diện tạo thành một đa diện có thể tích \(V'\). Tỉ số